
已建立动力学模型的类型 q 机制模型:根据反应机制建立 几乎没有 q 现象模型(经验模型):目前大多数模型 能定量地描述发酵过程 能反映主要因素的影响
已建立动力学模型的类型 q 机制模型:根据反应机制建立 几乎没有 q 现象模型(经验模型):目前大多数模型 能定量地描述发酵过程 能反映主要因素的影响
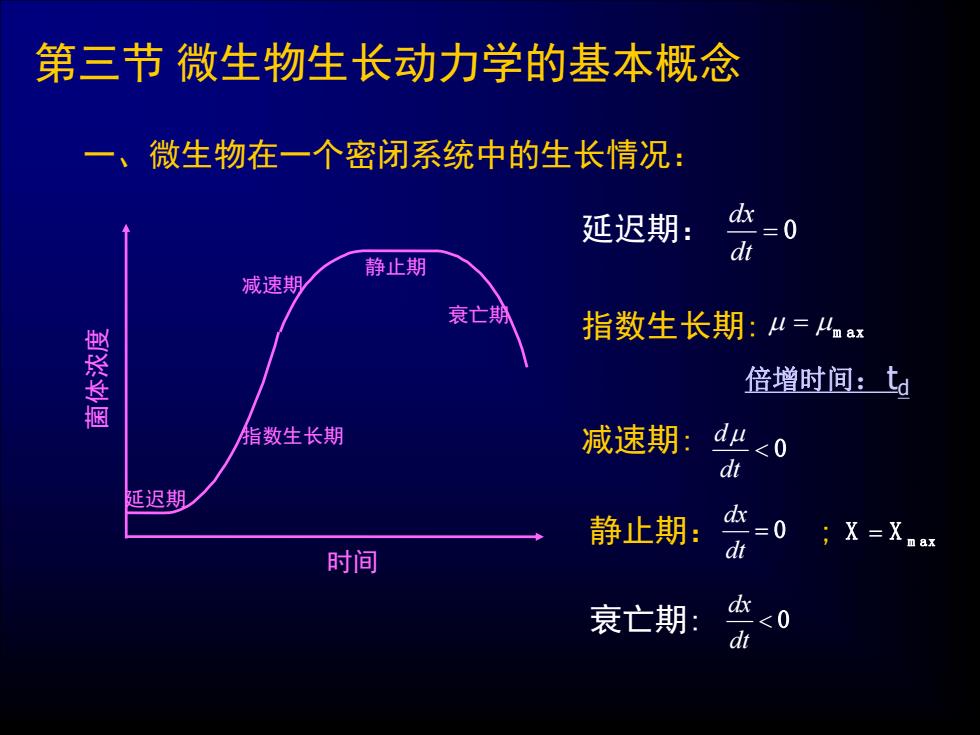
第三节 微生物生长动力学的基本概念 一、微生物在一个密闭系统中的生长情况: 时间 菌 体 浓 度 延迟期 指数生长期 减速期 静止期 衰亡期 延迟期: dx dt 0 指数生长期: m ax 倍增时间:td 减速期: d dt 0 静止期: ; dx dt 0 m ax X X 衰亡期: dx dt 0
第三节 微生物生长动力学的基本概念 一、微生物在一个密闭系统中的生长情况: 时间 菌 体 浓 度 延迟期 指数生长期 减速期 静止期 衰亡期 延迟期: dx dt 0 指数生长期: m ax 倍增时间:td 减速期: d dt 0 静止期: ; dx dt 0 m ax X X 衰亡期: dx dt 0

二、微生物的生长动力学、Monod方程 q 微生物的生长速度: μ=f(s,p,T,pH,.,) q 在一定条件下(基质限制): μ=f(S)
二、微生物的生长动力学、Monod方程 q 微生物的生长速度: μ=f(s,p,T,pH,.,) q 在一定条件下(基质限制): μ=f(S)
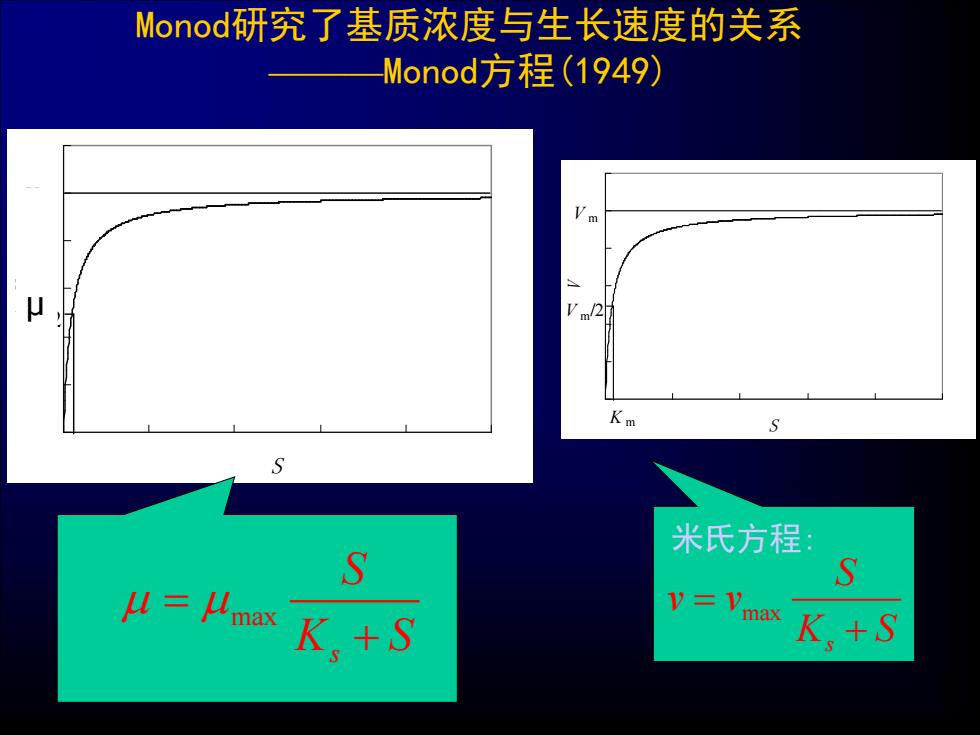
Monod研究了基质浓度与生长速度的关系 ———Monod方程(1949) 0 0.2 0.4 0.6 0.8 1 1.2 0 200 400 S 600 800 1000 V V m V m/2 K m 0 0.2 0.4 0.6 0.8 1 1.2 0 200 400 S 600 800 1000 V V m V m/2 K m μ max s S K S max s S v v K S 米氏方程:
Monod研究了基质浓度与生长速度的关系 ———Monod方程(1949) 0 0.2 0.4 0.6 0.8 1 1.2 0 200 400 S 600 800 1000 V V m V m/2 K m 0 0.2 0.4 0.6 0.8 1 1.2 0 200 400 S 600 800 1000 V V m V m/2 K m μ max s S K S max s S v v K S 米氏方程:
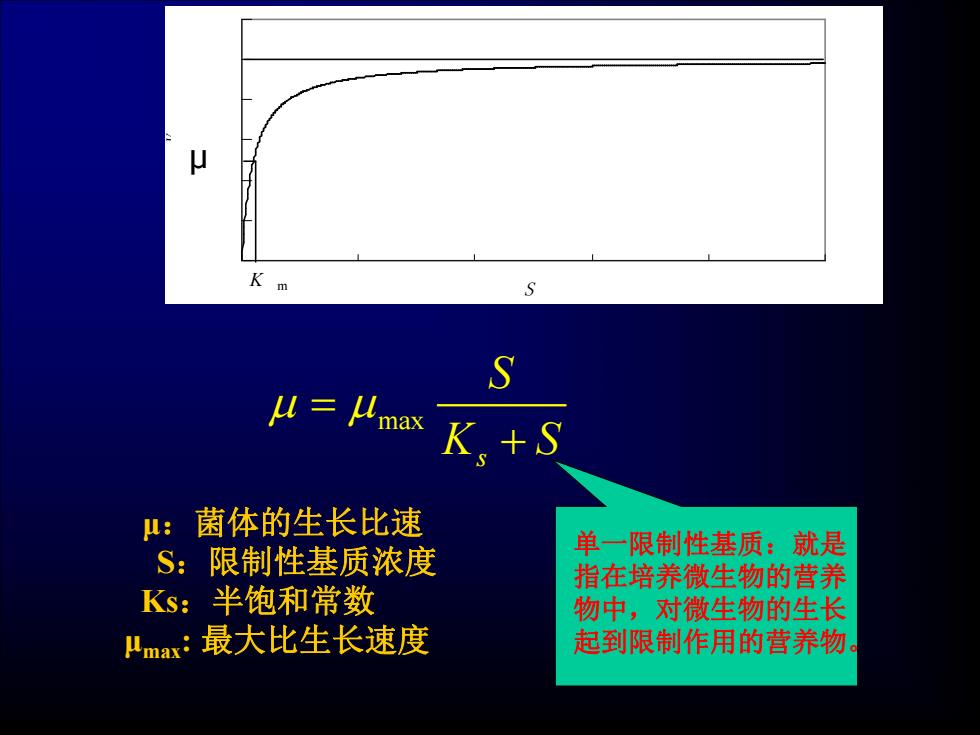
0 0 . 2 0 . 4 0 . 6 0 . 8 1 1 . 2 0 2 0 0 4 0 0 S 6 0 0 8 0 0 1 0 0 0 V V m V m / 2 K m max s S K S μ:菌体的生长比速 S:限制性基质浓度 Ks:半饱和常数 μmax: 最大比生长速度 μ 单一限制性基质:就是 指在培养微生物的营养 物中,对微生物的生长 起到限制作用的营养物
0 0 . 2 0 . 4 0 . 6 0 . 8 1 1 . 2 0 2 0 0 4 0 0 S 6 0 0 8 0 0 1 0 0 0 V V m V m / 2 K m max s S K S μ:菌体的生长比速 S:限制性基质浓度 Ks:半饱和常数 μmax: 最大比生长速度 μ 单一限制性基质:就是 指在培养微生物的营养 物中,对微生物的生长 起到限制作用的营养物