
第6章立体及其表面交线 本章内容是在研究点、线、面投影的基础上进一步论述立体的投影作图问题 6.1立体的投影 立体是由其表面所围成的。表面均为平面的立体称为平面立体,表面为曲面或平面与 曲面的立体称为曲面立体。在投影图上表示一个立体,就是把这些平面和曲面表达出来, 然后根据可见性原理判别线条的可见性,把其投影分别画成实线或虚线,即得立体的投影 图。 6.1.1.平面立体的投影 平面立体主要有棱柱、棱锥等。在投影图上表示平面立体就是把围成立体的平面及其 棱线表示出米,然后判别其可见性,把看得见的棱线投影画成实线,看不见的棱线的投影 画成虑线。 1.棱柱 (1)棱柱的投影图6-1为一正六棱柱,其顶面、底面均为水平面,它们的水平投影 反映实形,正面及侧面投影积聚为直线。棱柱有六个侧棱面,前后棱面为正平面,它们的 正面投影反映实形:水平及侧面投影积聚为一直线:棱柱的其它四个侧棱面均为铅垂面, 其水平投影均积聚为直线,正面和侧面投影均为类似形。 图61正六棱柱的投影及表面上取点 棱线AB为铅垂线,其水平投影积聚为一点ā(b),正面和侧面投影均反映实长,即 ab=ab守=AB。顶面的边DE为侧垂线,侧面投影积聚为一点d号(e),水平投影 和正面投影均反缺实长,即de=d件=DE。底面的边BC为水平线,水平投影反映实长, 即b=BC,正面投影bc4和侧面投影b背c均小于实长。其余棱线,可自行分析。 作图时可先画正六棱柱的水平投影正六边形,再根据投影规律作出其它两个投影。 (2)棱柱表面上取点在平面立体表面上取点,其原理和方法与在平面上取点相同。 30
130 第 6 章 立体及其表面交线 本章内容是在研究点、线、面投影的基础上进一步论述立体的投影作图问题。 6.1 立体的投影 立体是由其表面所围成的。表面均为平面的立体称为平面立体,表面为曲面或平面与 曲面的立体称为曲面立体。在投影图上表示一个立体,就是把这些平面和曲面表达出来, 然后根据可见性原理判别线条的可见性,把其投影分别画成实线或虚线,即得立体的投影 图。 6.1.1. 平面立体的投影 平面立体主要有棱柱、棱锥等。在投影图上表示平面立体就是把围成立体的平面及其 棱线表示出来,然后判别其可见性,把看得见的棱线投影画成实线,看不见的棱线的投影 画成虚线。 1.棱柱 (1)棱柱的投影 图 6-1 为一正六棱柱,其顶面、底面均为水平面,它们的水平投影 反映实形,正面及侧面投影积聚为直线。棱柱有六个侧棱面,前后棱面为正平面,它们的 正面投影反映实形;水平及侧面投影积聚为一直线;棱柱的其它四个侧棱面均为铅垂面, 其水平投影均积聚为直线,正面和侧面投影均为类似形。 棱线 AB 为铅垂线,其水平投影积聚为一点 a(b),正面和侧面投影均反映实长,即 ab=ab=AB。顶面的边 DE 为侧垂线,侧面投影积聚为一点 d (e),水平投影 和正面投影均反映实长,即 de=de=DE。底面的边 BC 为水平线,水平投影反映实长, 即 bc=BC,正面投影 bc和侧面投影 bc均小于实长。其余棱线,可自行分析。 作图时可先画正六棱柱的水平投影正六边形,再根据投影规律作出其它两个投影。 (2)棱柱表面上取点 在平面立体表面上取点,其原理和方法与在平面上取点相同。 d c m b c e n a d b c m a d n e n e m b a 图 6-1 正六棱柱的投影及表面上取点 a d e b c d a a (b) d (e ) b c (c) e H A B E C D V W

由于图6-1中所示正六棱柱的各个表面都处于特殊位置,因此在表面上取点可利用积聚性 原理作图。 如已知棱柱表面上点M的正面投影m1,要求出其它两投影m、m守。由于点M是可见 的,因此,点M必定在ABCD棱面上,而ABCD棱面为铅垂面,水平投影a(bcd有积聚 性,因此m必在a(bcd上,根据m和m即可求出m。又如已知点N的水平投影n, 要求出其它两投影nt、。由于点N是可见的,因此点N必定在顶面上,而顶面的正 面投影和侧面投影都具有积聚性,因此n、必定在顶面的同面投影上。 2.棱锥 (1)棱锥的投影如图6-2所示为一正三棱锥,锥顶为S,其底面为△4BC,呈水平 位置,其水平投影△abc反映实形。棱面△SAB、△SBC是一般位置平面,它们的各个投影 均为类似形。棱面△SAC为侧垂面,其侧面投影△sac“积聚为一直线。底边AB、BC 为水平线,CA为侧垂线,棱线SB为侧平线,SA、SC为倾斜线,它们的投影可根据不同 位置直线的投影特性进行分析 作图时先画出底面△ABC的各个投影,再作出锥顶S的各个投影,然后连接各棱线即 图62正三棱锥的投影及表面取点图 得正三棱锥的三面投影 (2)棱锥表面上取点如已知点M的正面投影mA,要求出点M的其它投影m,m: 由于点M在棱面△S4B上,因此过点M在△SAB上作AB的平行线IM,即作1mA∥abM, 再作lm∥ab,求出m,再根据m、mt求出m。也可过锥顶S和点M作一辅助线S 然后求出点M的水平投影m,再由m、mA求出点M的侧面投影m逍。又如已知点N的水 平投影n,要求出点N的其它投影n、n。由于点N在侧垂面△SAC上,因此n必定在 △s尚ac当上,由n、n进可求出(n4)。 6.1.2曲面立体的投影 工程中常见的曲面立体是回转体,主要有圆柱、圆锥、球、环等,在投影图上表示回 转体就是把组成立体的回转面或平面和回转面表示出来,然后判别其可见性。 1.圆柱圆柱表面由圆柱面和项、底圆所组成。圆柱面是一直母线绕与之平行的轴线 回转而成,如图6-3a所示。 (1)圆柱的投影如图6-3b所示,圆柱的轴线垂直于H面,其上、下底圆为水平面, 水平投影反映实形,其正面和侧面投影积聚为一直线。圆柱面的水平投影也积聚为一圆 13
131 由于图 6-1 中所示正六棱柱的各个表面都处于特殊位置,因此在表面上取点可利用积聚性 原理作图。 如已知棱柱表面上点 M 的正面投影 m,要求出其它两投影 m、m。由于点M是可见 的,因此,点 M 必定在 ABCD 棱面上,而 ABCD 棱面为铅垂面,水平投影 a(b)(c)d 有积聚 性,因此 m 必在 a(b)(c)d 上,根据 m和 m 即可求出 m。又如已知点 N 的水平投影 n, 要求出其它两投影 n、 n。由于点 N 是可见的,因此点 N 必定在顶面上,而顶面的正 面投影和侧面投影都具有积聚性,因此 n、n必定在顶面的同面投影上。 2.棱锥 (1)棱锥的投影 如图 6-2 所示为一正三棱锥,锥顶为 S,其底面为△ABC,呈水平 位置,其水平投影△abc 反映实形。棱面△SAB、△SBC 是一般位置平面,它们的各个投影 均为类似形。棱面△SAC 为侧垂面,其侧面投影△sac"积聚为一直线。底边 AB、BC 为水平线,CA 为侧垂线,棱线 SB 为侧平线,SA、SC 为倾斜线,它们的投影可根据不同 位置直线的投影特性进行分析。 作图时先画出底面△ABC 的各个投影,再作出锥顶 S 的各个投影,然后连接各棱线即 得正三棱锥的三面投影。 (2)棱锥表面上取点 如已知点M的正面投影 m,要求出点 M 的其它投影 m、m。 由于点 M 在棱面△SAB 上,因此过点M在△SAB 上作 AB 的平行线ⅠM,即作 1m∥ab, 再作 1m∥ab,求出 m,再根据 m、m求出 m。也可过锥顶 S 和点 M 作一辅助线 SⅡ, 然后求出点 M 的水平投影 m,再由 m、m求出点 M 的侧面投影 m。又如已知点 N 的水 平投影 n,要求出点 N 的其它投影 n、n。由于点 N 在侧垂面△SAC 上,因此 n必定在 △sac上,由 n、n可求出(n)。 6.1.2 曲面立体的投影 工程中常见的曲面立体是回转体,主要有圆柱、圆锥、球、环等,在投影图上表示回 转体就是把组成立体的回转面或平面和回转面表示出来,然后判别其可见性。 1.圆柱 圆柱表面由圆柱面和顶、底圆所组成。圆柱面是一直母线绕与之平行的轴线 回转而成,如图 6-3a 所示。 (1)圆柱的投影 如图 6-3b 所示,圆柱的轴线垂直于 H 面,其上、下底圆为水平面, 水平投影反映实形,其正面和侧面投影积聚为一直线。圆柱面的水平投影也积聚为一圆, c a b m n s s n m b c a 2 1 n s m 2 c b a 图 6-2 正三棱锥的投影及表面取点图 a s b s a a c s b (c ) b H A B C S V W
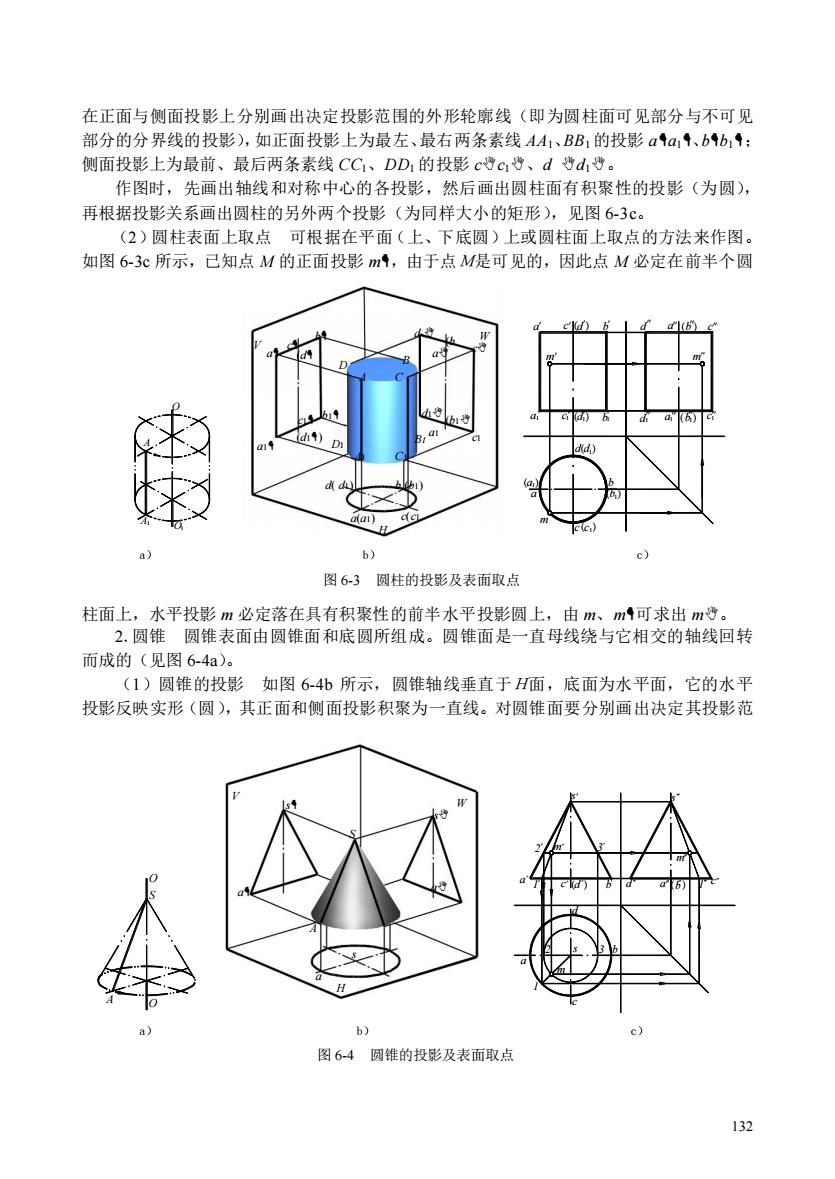
在正面与侧面投影上分别画出决定投影范围的外形轮廓线(即为圆柱面可见部分与不可见 部分的分界线的投景影),如正面投影上为最左、最右两条素线AA1、BB,的投影aa,、bb,年: 训面投母影上为最前、最后两条素线CC,、DD,的投号影c物C、d特d,博。 作图时,先画出轴线和对称中心的各投影,然后画出圆柱面有积聚性的投影(为圆), 再根据投影关系画出圆柱的另外两个投影(为同样大小的矩形),见图6-3c。 (2)圆柱表面上取点可根据在平面(上、下底圆)上或圆柱面上取点的方法来作图 如图6-3C所示,己知点M的正面投影m1,由于点M是可见的,因此点M必定在前半个圆 b) 图63圆柱的投影及表面取点 柱面上,水平投影m必定落在具有积聚性的前半水平投影圆上,由m、m可求出m增。 2.圆锥圆锥表面由圆锥面和底圆所组成。圆锥面是一直母线绕与它相交的轴线回转 而成的(见图64a)。 (1)圆锥的投影如图6-4b所示,圆锥轴线垂直于H面,底面为水平面,它的水平 投影反映实形(圆),其正面和侧面投影积聚为一直线。对圆锥面要分别画出决定其投影范 b) 图64圆锥的投影及表面取点 132
132 在正面与侧面投影上分别画出决定投影范围的外形轮廓线(即为圆柱面可见部分与不可见 部分的分界线的投影),如正面投影上为最左、最右两条素线 AA1、BB1 的投影 aa1、bb1; 侧面投影上为最前、最后两条素线 CC1、DD1 的投影 cc1、d d1。 作图时,先画出轴线和对称中心的各投影,然后画出圆柱面有积聚性的投影(为圆), 再根据投影关系画出圆柱的另外两个投影(为同样大小的矩形),见图 6-3c。 (2)圆柱表面上取点 可根据在平面(上、下底圆)上或圆柱面上取点的方法来作图。 如图 6-3c 所示,已知点 M 的正面投影 m,由于点M是可见的,因此点 M 必定在前半个圆 柱面上,水平投影 m 必定落在具有积聚性的前半水平投影圆上,由 m、m可求出 m。 2.圆锥 圆锥表面由圆锥面和底圆所组成。圆锥面是一直母线绕与它相交的轴线回转 而成的(见图 6-4a)。 (1)圆锥的投影 如图 6-4b 所示,圆锥轴线垂直于H面,底面为水平面,它的水平 投影反映实形(圆),其正面和侧面投影积聚为一直线。对圆锥面要分别画出决定其投影范 O O A A 1 1 a b c d m a c d b m d a b c m ( ) ( ) a c (d ) b d a (b ) 1 1 1 1 c 1 1 1 1 (a1) (d1) (b1) (c1) a) b) c) 图 6-3 圆柱的投影及表面取点 O S A O a b c d s m 2 3 1 s 3 c d b 2 m a 1 s m c ( ) d a (b) 1 a) b) c) 图 6-4 圆锥的投影及表面取点 a (d ) b c d a(a1) a d( d1) (b1) (b ) c c(c1 ) H A B C D V W (d1) b1 c1 a1 d1 a1 (b1 ) c1 b A1 B1 C1 D1 a s s a a s H A S V W

围的外形轮廓线,如正面投影上为最左、最右两条素线S4、SB的投影sa4、s4bM,侧面 投影上为最前、最后两条素线SC、SD的投影sc、sd曹。 作图时,先画出轴线和对称中心的各投影:然后画出底面的各个投影及锥顶点的投影, 再分别画出其外形轮廓线,即完成圆锥的各个投影(见图64c)。 (2)圆锥表面上取点 可根据圆锥面的形成特性来作图。如图6-4c所示,己知圆细 面上点M的正面投影mA,可采用下列两种方法求出点M的水平投影m和侧面投影m净。 方法一:辅助素线法过锥顶S和点M作一辅助线SI,根据已知条件可以确定S的 正面投影s411,然后求出它的水平投影s1、侧面投影s1边,再由m4根据点在直线上的 投影性质求出m和m。 方法二:辅助圆法过点M作一平行于底面的水平辅助圆,该圆的正面投影为过m 且平行于4b4的直线2431,它的水平投影为一直径等于231的圆,m必在此圆周上,由 m求出m,再由m、m求出m。 3.球球的表面是球面。球面是一个圆母线绕其过圆心且在同一平面上的轴线回转而 形成的(图6-5a)。 (1)球的投影如图65b所示,球的三个投影均为圆,其直径与球直径相等,但三 个投影面上的圆是不同的转向线的投影,正面投影上的圆是平行于V面的最大圆的投影 b) c) 图65球的投形及表面取点 (区分前、后半球表面的外形轮廓线),水平投影上的圆是平行于H面的最大圆的投影(区 分上、下半球表面的外形轮廓线),侧面投影上的圆是平行于W面的最大圆的投影(区别 左、右半球表面的外形轮廓线)。 作图时,可先画出确定球心的三个投影,再以球心为圆心画出三个与圆球直径相等的 圆。 (2)球面上取点如图6-5c所示,己知球面上点M的水平投影m,要求出其m4和 m遗。可过点M作一平行于V面的辅助圆,它的水平投影为12,正面投影为直径等于121 的圆,m必定在该圆上,由m可求得m,由m和m可求出m3。显然,点M在前半球 面上,因此从前向后看是可见的,同理,点M在左半球面上,从左向右看也是可见的。 当然,也可作平行于H面的辅助圆来作图,读者自行分析并想像当点位于后半球时, 133
133 围的外形轮廓线,如正面投影上为最左、最右两条素线 SA、SB的投影 sa、sb,侧面 投影上为最前、最后两条素线 SC、SD 的投影 sc、sd 。 作图时,先画出轴线和对称中心的各投影;然后画出底面的各个投影及锥顶点的投影, 再分别画出其外形轮廓线,即完成圆锥的各个投影(见图 6-4c)。 (2)圆锥表面上取点 可根据圆锥面的形成特性来作图。如图 6-4c 所示,己知圆锥 面上点M的正面投影 m,可采用下列两种方法求出点 M 的水平投影 m 和侧面投影 m。 方法一:辅助素线法 过锥顶 S 和点 M 作一辅助线 SI,根据已知条件可以确定 SI 的 正面投影 s1,然后求出它的水平投影 s1、侧面投影 s1,再由 m根据点在直线上的 投影性质求出 m 和 m。 方法二:辅助圆法 过点 M 作一平行于底面的水平辅助圆,该圆的正面投影为过 m 且平行于 ab的直线 23,它的水平投影为一直径等于 23的圆,m 必在此圆周上,由 m求出 m,再由 m、 m 求出 m。 3.球 球的表面是球面。球面是一个圆母线绕其过圆心且在同一平面上的轴线回转而 形成的(图 6-5a)。 (1)球的投影 如图 6-5b 所示,球的三个投影均为圆,其直径与球直径相等,但三 个投影面上的圆是不同的转向线的投影,正面投影上的圆是平行于 V 面的最大圆的投影 (区分前、后半球表面的外形轮廓线),水平投影上的圆是平行于 H 面的最大圆的投影(区 分上、下半球表面的外形轮廓线),侧面投影上的圆是平行于 W 面的最大圆的投影(区别 左、右半球表面的外形轮廓线)。 作图时,可先画出确定球心的三个投影,再以球心为圆心画出三个与圆球直径相等的 圆。 (2)球面上取点 如图 6-5c 所示,已知球面上点 M 的水平投影 m,要求出其 m和 m。可过点 M 作一平行于 V 面的辅助圆,它的水平投影为 12,正面投影为直径等于 12 的圆,m必定在该圆上,由 m 可求得 m,由 m 和 m可求出 m。显然,点 M 在前半球 面上,因此从前向后看是可见的,同理,点 M 在左半球面上,从左向右看也是可见的。 当然,也可作平行于 H 面的辅助圆来作图,读者自行分析并想像当点位于后半球时, O O C B A 1 m e o 2 d m 1 o 2 f o m a) b) c) 图 6-5 球的投影及表面取点 H V W
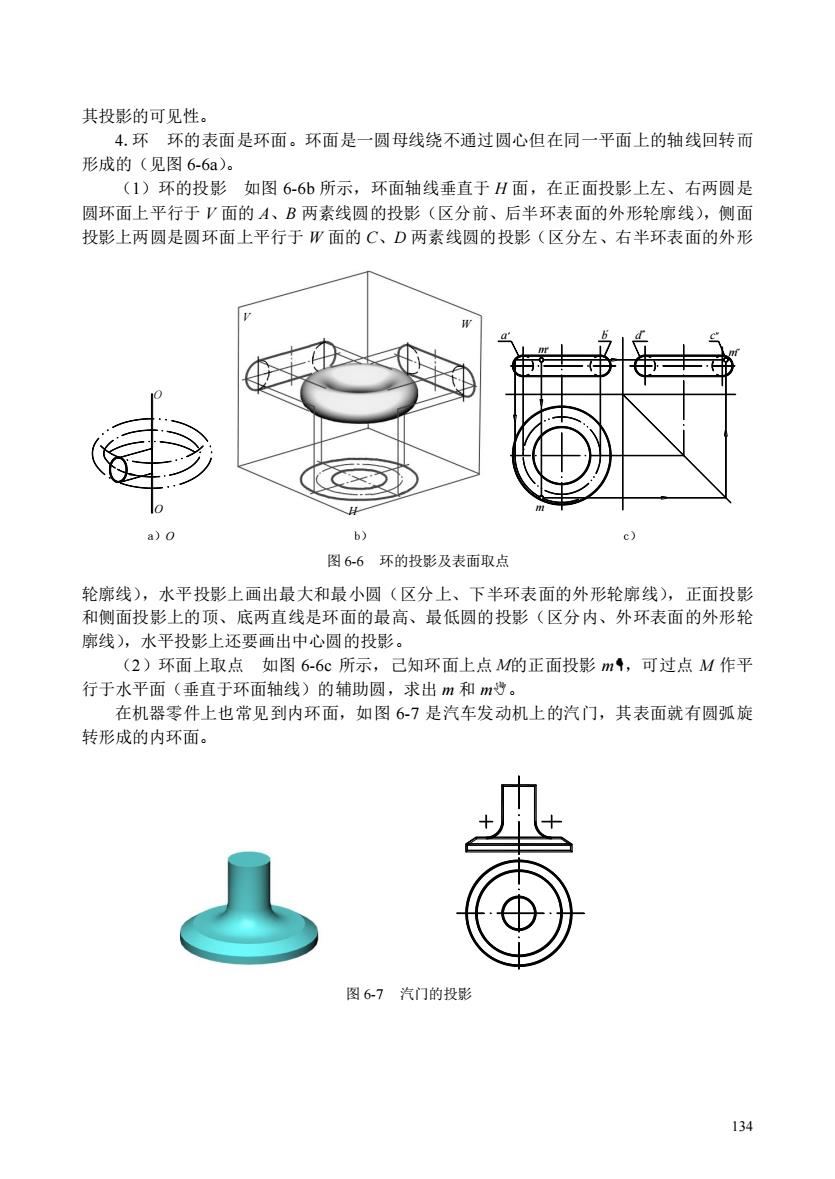
其投影的可见性 4.环环的表面是环面。环面是一圆母线绕不通过圆心但在同一平面上的轴线回转而 形成的(见图6-6a)。 (1)环的投影 如图66b所示,环面轴线垂直于H面,在正面投影上左、右两圆是 圆环面上平行于V面的A、B两素线圆的投影(区分前、后半环表面的外形轮廓线),侧面 投影上两圆是圆环面上平行于W面的C、D两素线圆的投影(区分左、右半环表面的外形 c) 图6-6环的投影及表面取点 轮廓线),水平投影上画出最大和最小圆(区分上、下半环表面的外形轮廓线),正面投影 和侧面投影上的顶、底两直线是环面的最高、最低圆的投影(区分内、外环表面的外形轮 廓线),水平投影上还要画出中心圆的投影。 (2)环面上取点如图6-6c所示,己知环面上点M的正面投影m1,可过点M作平 行于水平面(垂直于环面轴线)的辅助圆,求出m和m。 在机器零件上也常见到内环面,如图67是汽车发动机上的汽门,其表面就有圆弧旋 转形成的内环面。 图67汽门的投影
134 其投影的可见性。 4.环 环的表面是环面。环面是一圆母线绕不通过圆心但在同一平面上的轴线回转而 形成的(见图 6-6a)。 (1)环的投影 如图 6-6b 所示,环面轴线垂直于 H 面,在正面投影上左、右两圆是 圆环面上平行于 V 面的 A、B 两素线圆的投影(区分前、后半环表面的外形轮廓线),侧面 投影上两圆是圆环面上平行于 W 面的 C、D 两素线圆的投影(区分左、右半环表面的外形 轮廓线),水平投影上画出最大和最小圆(区分上、下半环表面的外形轮廓线),正面投影 和侧面投影上的顶、底两直线是环面的最高、最低圆的投影(区分内、外环表面的外形轮 廓线),水平投影上还要画出中心圆的投影。 (2)环面上取点 如图 6-6c 所示,己知环面上点M的正面投影 m,可过点 M 作平 行于水平面(垂直于环面轴线)的辅助圆,求出 m 和 m。 在机器零件上也常见到内环面,如图 6-7 是汽车发动机上的汽门,其表面就有圆弧旋 转形成的内环面。 O m a m b d c m a)O b) c) 图 6-6 环的投影及表面取点 图 6-7 汽门的投影 H V W