
电子种越女学 University of Electroale Science and Technelery of China 986 Chapter 4 Retiming Dr.Ling National Key Lab of Science and Technology on Communication
Chapter 4 Retiming Dr. Ling National Key Lab of Science and Technology on Communication
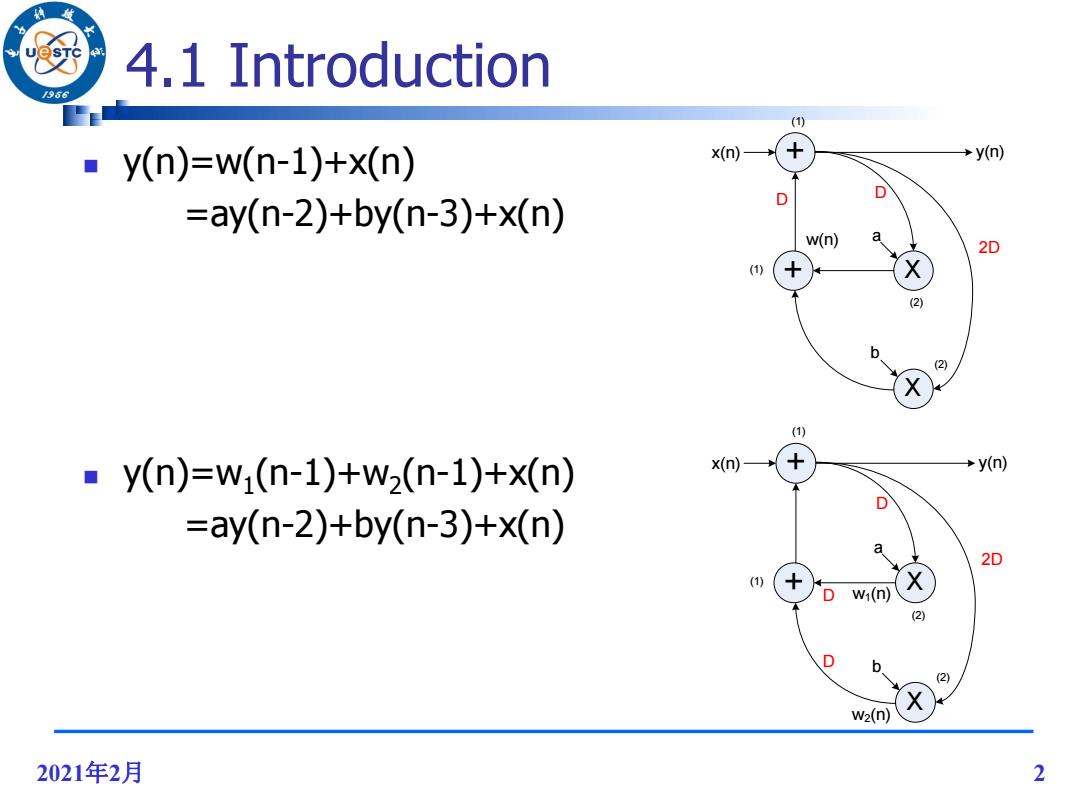
43 4.1 Introduction 96 () y(n)=w(n-1)+x(n) x(n) →yn) D D =ay(n-2)+by(n-3)+x(n) w(n) a 2D (1) (2) b (2) (1) ay(n)=w(n-1)+w2(n-1)+x(n) x(n) →yn) D =ay(n-2)+by(n-3)+x(n) a 2D (1) w(n) (2) (2) w2(n) 2021年2月 2
2021年2月 2 4.1 Introduction y(n)=w(n-1)+x(n) =ay(n-2)+by(n-3)+x(n) y(n)=w1 (n-1)+w2 (n-1)+x(n) =ay(n-2)+by(n-3)+x(n) + X + X D D 2D (1) (1) (2) (2) x(n) y(n) a b w(n) + X + X D D 2D (1) (1) (2) (2) x(n) y(n) a b w1(n) D w2(n)

Retiming? /96 Retiming is a transformation technique used to change the locations of delay elements in a circuit without affection the input/output characteristics of the circuit. Retiming has many applications in synchronous circuit design,including reducing the clock period of the circuit, reducing the number of registers in the circuit, -reducing the power consumption of the circuit, logic synthesis. 2021年2月 3
2021年2月 3 Retiming? Retiming is a transformation technique used to change the locations of delay elements in a circuit without affection the input/output characteristics of the circuit. Retiming has many applications in synchronous circuit design, including reducing the clock period of the circuit, reducing the number of registers in the circuit, reducing the power consumption of the circuit, logic synthesis
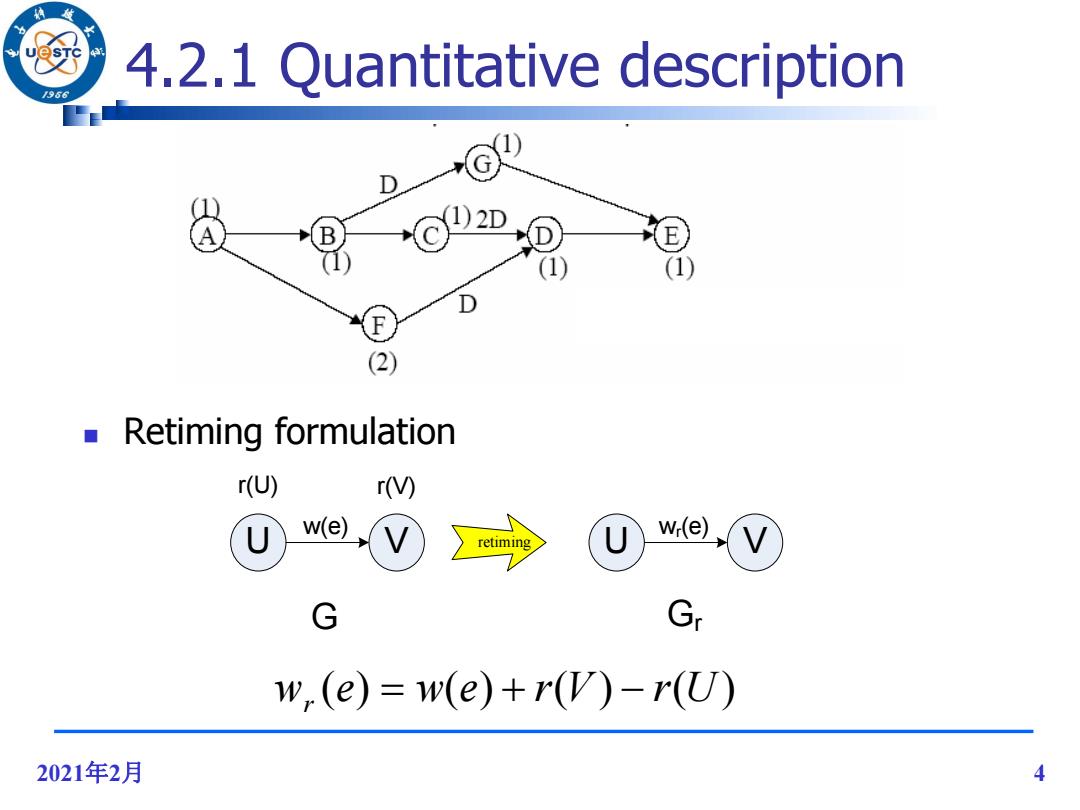
4.2.1 Quantitative description 966 1)2D 1) (1) D (2) Retiming formulation r(U) r U w(e) V U w(e) retiming V G Gr w,(e)=w(e)+r(V)-r(U) 2021年2月 4
2021年2月 4 4.2.1 Quantitative description Retiming formulation w (e) w(e) r(V) r(U) r U V w(e) r(U) r(V) retiming U V wr(e) G Gr

(1) /96 ■Letr(1)=0,r(2)=1,r(3)=0,r(4)=0 D (1) (2) 2D w,(3→2)=1w(3→2)+r(2)-r(3)=0+1-0=1 2 3 w,(4→2)=w(4→2)+r(2)-r(4)=0+1-0=1 w,(2→1)=w(2→1)+r(1)-r(2)=1+0-1=0 (2) (1) A retiming solution is feasible only if w-(e)>0 holds for all edges. (1) (2) 2D How to determine the retiming value,r(V),will be 2 3 discussed in section 4.4.2.And the method of solving systems of inequalities is used,which will be given in section 4.3. D (2) 2021年2月 5
2021年2月 5 Let r(1)=0, r(2)=1, r(3)=0, r(4)=0 A retiming solution is feasible only if wr (e)≥0 holds for all edges. How to determine the retiming value, r(V), will be discussed in section 4.4.2. And the method of solving systems of inequalities is used, which will be given in section 4.3. 1 4 2 3 D D 2D (1) (1) (2) (2) D w (3 2) w(3 2) r(2) r(3) 0 1 0 1 r wr (4 2) w(4 2) r(2) r(4) 0 1 0 1 1 4 2 3 D D 2D (1) (1) (2) (2) wr (2 1) w(2 1) r(1) r(2) 1 0 1 0