延安大学化学与化工学院：《物理化学》课程教学资源（电子教案讲稿）第二章 热力学第一定律

延安大学精品课程…物理化学 表面功 y(表面张力) d4(面积的改变) ydA 7.常用的徽分公式 ①全微分方程：设H=f(T,p),丽=识】 dT+ dp (2)设：Z=f(T,p),则dZ= dT+ ap (3)判断状态函数的原则：二阶偏导与求导顺序无关（全微分性质） )- ④倒数关系 9福环关系：设：U=f,n,)〔部)〔)，=- (6)链关系：严-少（引入第三个变量） dt dy dt 2.4 热力学第一定律 一、热功当量 焦耳(Joule)和迈耶尔(Mayer)自1840年起，历经20多年，用各种实验求证热和功的转换关系， 得到的结果是一致的。 即：1cal=4.1840J 这就是著名的热功当量，为能量守恒原理提供了科学的实验证明。 现在，国际单位制中已不用cl,热功当量这个词将逐渐被废除。 二、能量守恒定律 到1850年，科学界公认能量守恒定律是自然界的普遍规律之一。能量守恒与转化定律可表述为： 自然界的一切物质都具有能量，能量有各种不同形式，能够从一种形式转化为另一种形式，但在转 化过程中，能量的总值不变。 三、体系的能量 体系的能量由下列三部分组成 (1)系统整体运动的动能(T): (2)系统在外力场中的位能(V): (3)热力学能(U),也称内能： 第11页共75页

延安大学精品课程 …… 物理化学 第 11 页 共 75 页 表面功 γ（表面张力） dA（面积的改变） γdA 7. 常用的微分公式 dp p H dT T H H f T p dH p T            +        （1）全微分方程：设 = （ ， ）， = p T Z Z Z = f T p dZ = dT dp T p        +         （2）设： （ ， ），则 （3）判断状态函数的原则：二阶偏导与求导顺序无关(全微分性质) p T T p Z Z Z Z p T T p                 =                   4 = 1                   V V p T T p （）倒数关系： 5  = −1                        = V U U T V V T T U （）循环关系：设：U f（T，V），则 6 dZ dZ dy dt dy dt （ ）链关系： = （引入第三个变量） 2.4 热力学第一定律 一、热功当量 焦耳（Joule）和迈耶尔(Mayer)自 1840 年起，历经 20 多年，用各种实验求证热和功的转换关系， 得到的结果是一致的。 即： 1 cal = 4.1840 J 这就是著名的热功当量，为能量守恒原理提供了科学的实验证明。 现在，国际单位制中已不用 cal，热功当量这个词将逐渐被废除。 二、能量守恒定律 到 1850 年，科学界公认能量守恒定律是自然界的普遍规律之一。能量守恒与转化定律可表述为： 自然界的一切物质都具有能量，能量有各种不同形式，能够从一种形式转化为另一种形式，但在转 化过程中，能量的总值不变。 三、体系的能量 体系的能量由下列三部分组成 （1）系统整体运动的动能（T）； （2）系统在外力场中的位能（V）； （3）热力学能（U），也称内能；

延安大学精品课程…物理化学 即：E=T+V+UU 热力学研究的对象：宏观静止、无整体运动的系统，并且一般不存在特殊的外力场，故只考虑热 力学能。 四、热力学能 热力学能(thermodynamic energy)以前称为内能(internal energy),它是指体系内部能量的总和， 包括分子运动的平动能、转动能、振动能、电子能、核能以及各种粒子之间的相互作用位能等。 热力学能是状态函数，用符号U表示，是系统的自身性质，只决定于其状态，是系统状态的单值函 数，在定态下有定值。它的绝对值尚无法测定，只能求出它的变化值。 对纯物质的均相系统，U是P、V、T中任意两个独立变量再加上物质的量n的函数。即U=∫(T, V,n) 五、热力学第一定律 文字表述：是能量守恒与转化定律在热现象领域内所具有的特殊形式，说明热力学能、热和功之间 可以相互转化，但总的能量不变。 热力学第一定律表述：第一类永动机是不可能制成的。 第一类永动机：一种既不靠外界提供能量，本身也不减少能量，却可以不断对外作功的机器称为第 一类永动机，它显然与能量守恒定律矛盾。 历史上曾一度热衷于制造这种机器，均以失败告终，也就证明了能量守恒定律的正确性。 第一定律的数学表达式△U=Q+W 对微小变化：dU=6Q+8W 因为热力学能是状态函数，数学上具有全微分性质，微小变化可用dU表示：Q和W不是状态函数， 微小变化用8表示，以示区别。 说明：(1)适用于封闭体系，也可适用于孤立系统 (2)W总功，W=W。+W, (3)虽然Q与W是过程变量，但Q一W只决定于始终态。 补充：证明U是状态函数（反证法） 2.5准备静态过程与可逆过程 一、功与过程 设在定温下，一定量理想气体在活塞筒中克服外压，经4种不同途径，体积从1膨胀到2所作 的功。 1.自由膨胀（向真空膨胀） 6W1=-p.dV=0因为ps=0,所以，W=0。 2.等外压膨胀(P。保持不变) W2=-P2(V2-) 第12页共75页 P 阴形面积代表用

延安大学精品课程 …… 物理化学 第 12 页 共 75 页 即：E=T+V+U 热力学研究的对象：宏观静止、无整体运动的系统，并且一般不存在特殊的外力场，故只考虑热 力学能。 四、热力学能 热力学能（thermodynamic energy）以前称为内能（internal energy）,它是指体系内部能量的总和， 包括分子运动的平动能、转动能、振动能、电子能、核能以及各种粒子之间的相互作用位能等。 热力学能是状态函数，用符号 U 表示，是系统的自身性质，只决定于其状态，是系统状态的单值函 数，在定态下有定值。它的绝对值尚无法测定，只能求出它的变化值。 对纯物质的均相系统， U 是 P、V、T 中任意两个独立变量再加上物质的量 n 的函数。即 U=f（T， V，n） 五、热力学第一定律 文字表述：是能量守恒与转化定律在热现象领域内所具有的特殊形式，说明热力学能、热和功之间 可以相互转化，但总的能量不变。 热力学第一定律表述：第一类永动机是不可能制成的。 第一类永动机：一种既不靠外界提供能量，本身也不减少能量，却可以不断对外作功的机器称为第 一类永动机，它显然与能量守恒定律矛盾。 历史上曾一度热衷于制造这种机器，均以失败告终，也就证明了能量守恒定律的正确性。 第一定律的数学表达式 U = Q + W 对微小变化： dU =Q +W 因为热力学能是状态函数，数学上具有全微分性质，微小变化可用 dU 表示；Q 和 W 不是状态函数， 微小变化用  表示，以示区别。 说明：（1）适用于封闭体系，也可适用于孤立系统 （2）W 总功，W＝We ＋ W f （3）虽然 Q 与 W 是过程变量，但 Q－W 只决定于始终态。 补充：证明 U 是状态函数（反证法） 2.5 准备静态过程与可逆过程 一、功与过程 设在定温下，一定量理想气体在活塞筒中克服外压 ,经 4 种不同途径，体积从 V1 膨胀到 V2 所作 的功。 1.自由膨胀 （向真空膨胀） 因为 pe ＝0，所以，W＝0。 2.等外压膨胀（pe保持不变） δ d 0 W p V e,1 e = − = e,2 2 2 1 W p V V = − − ( ) pV1 1 p2 V1 V2 V p pV2 2 We,2

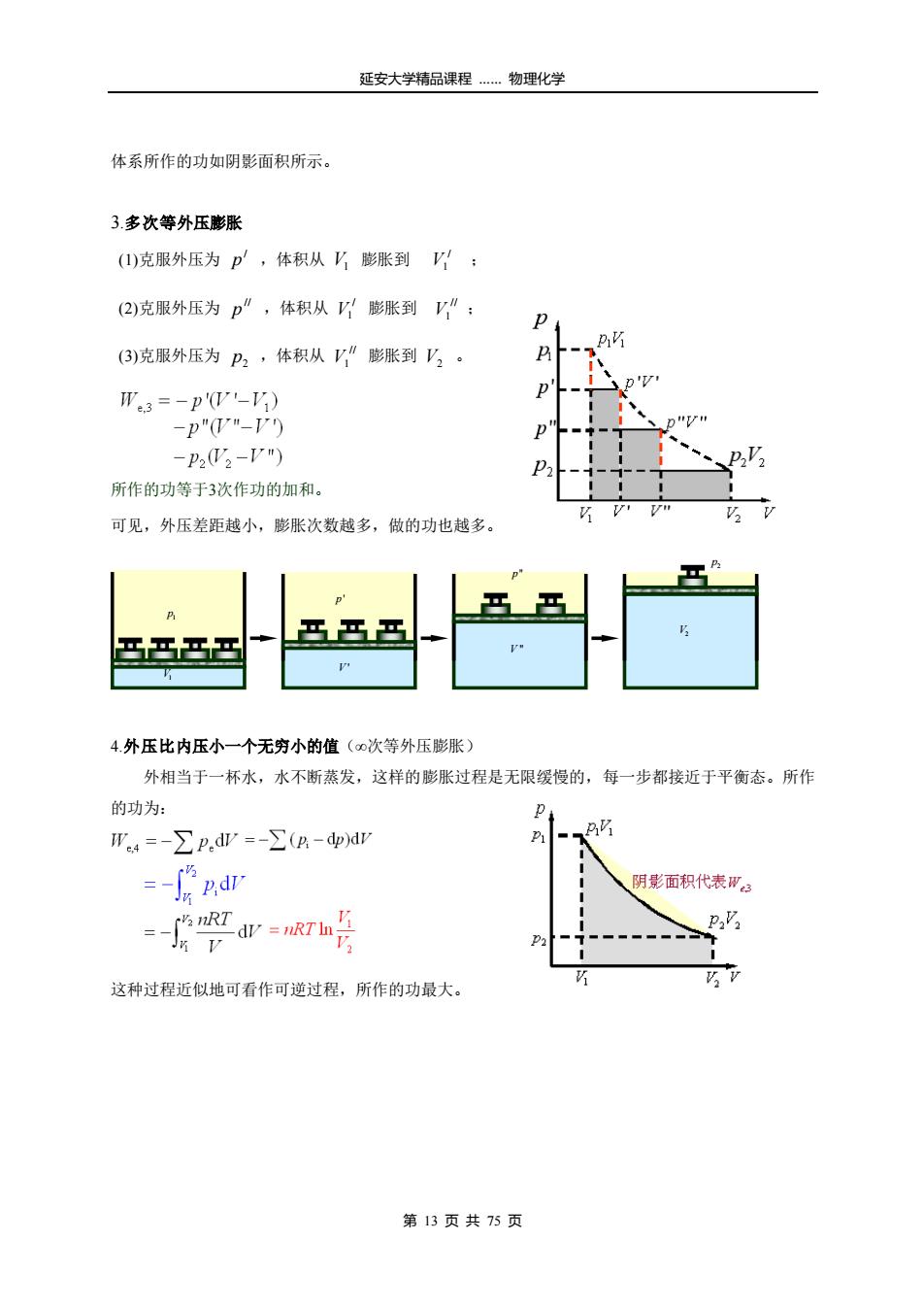
延安大学精品课程…物理化学 体系所作的功如阴影面积所示。 3.多次等外压膨胀 (1)克服外压为p,体积从V膨胀到V: (2)克服外压为p”，体积从膨胀到V”: P 巧 (3)克服外压为P2,体积从V”膨胀到V2。 W3=-p'W-') -p"W"-V) -P22-V") 所作的功等于3次作功的加和。 可见，外压差距越小，膨胀次数越多，做的功也越多。 D 马马马马 4.外压比内压小一个无穷小的值(0次等外压膨胀) 外相当于一杯水，水不断蒸发，这样的膨胀过程是无限缓慢的，每一步都接近于平衡态。所作 的功为： p We4=-∑p.dr=-∑(g-dp)dr hndr 阴影面积代表W RT =T 三JV 这种过程近似地可看作可逆过程，所作的功最大。 第13页共75页

延安大学精品课程 …… 物理化学 第 13 页 共 75 页 体系所作的功如阴影面积所示。 3.多次等外压膨胀 (1)克服外压为 / p ，体积从 V1 膨胀到 / V1 ； (2)克服外压为 // p ，体积从 / V1 膨胀到 // V1 ； (3)克服外压为 2 p ，体积从 // V1 膨胀到 V2 。 所作的功等于3次作功的加和。 可见，外压差距越小，膨胀次数越多，做的功也越多。 4.外压比内压小一个无穷小的值（∞次等外压膨胀） 外相当于一杯水，水不断蒸发，这样的膨胀过程是无限缓慢的，每一步都接近于平衡态。所作 的功为： 这种过程近似地可看作可逆过程，所作的功最大。 1 p V1 p ' V ' p " V " p2 V2

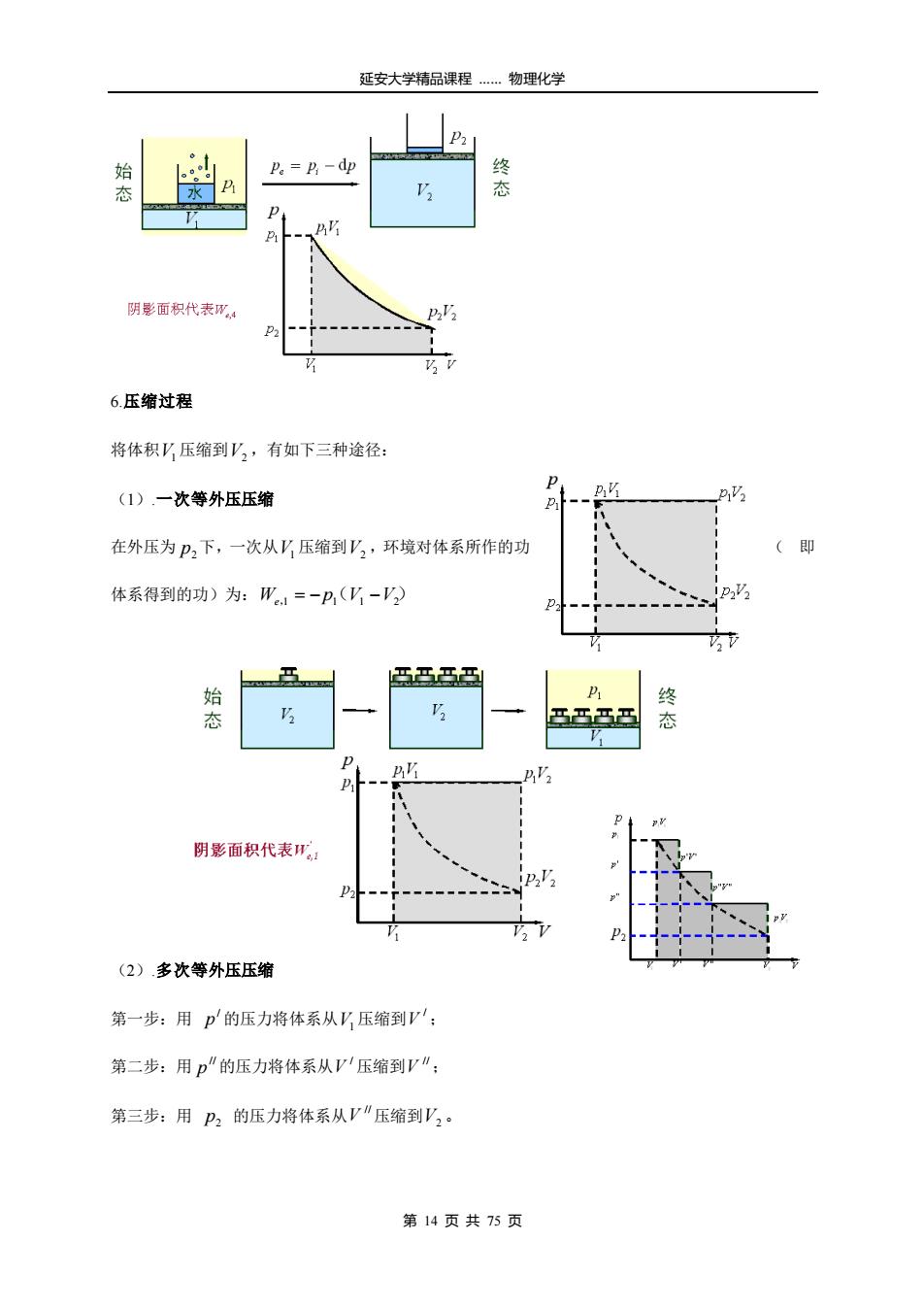
延安大学精品课程…物理化学 始 P。=-dp 水 态 B P 阴影面积代表W4 6.压缩过程 将体积V压缩到V,,有如下三种途径： P (1).一次等外压压缩 2 在外压为P2下，一次从？压缩到'2，环境对体系所作的功 (即 体系得到的功)为：W=-P,(V,-V) P23 臣马马臣 终 态 马马马马 态 P 阴影面积代表Ha (2)多次等外压压缩 第一步：用p的压力将体系从V压缩到V': 第二步：用p"的压力将体系从V压缩到V": 第三步：用P2的压力将体系从V"压缩到V2。 第14页共75页

延安大学精品课程 …… 物理化学 第 14 页 共 75 页 6.压缩过程 将体积 V1 压缩到 V2 ，有如下三种途径： （1）.一次等外压压缩 在外压为 p2 下，一次从 V1 压缩到 V2 ，环境对体系所作的功 （ 即 体系得到的功）为： We，1 = −p（1 V1 −V2） （2）.多次等外压压缩 第一步：用 / p 的压力将体系从 V1 压缩到 / V ； 第二步：用 // p 的压力将体系从 / V 压缩到 // V ； 第三步：用 2 p 的压力将体系从 // V 压缩到 V2

延安大学精品课程…物理化学 W1=-p(W'-T2) -p(V'-V') AD' D -h(-V) 整个过程所作的功为三步加和。 (3)可逆压缩 如果将蒸发掉的水气慢慢在杯中凝聚，使压力缓 慢增加， 阴影面积代表W4 恢复到原状，所作的功为： W=- p,dy nRT I 则体系和环境都能恢复到原状。 P。=P,+dp 态 D 终 P 阴影面积代表W 功与过程小结： 从以上的膨胀与压缩过程看出，功与变化的途径有关。虽然始终态相同，但途径不同，所作的功也 大不相同。显然，可逆膨胀，体系对环境作最大功：可逆压缩，环境对体系作最小功。 第15页共75页

延安大学精品课程 …… 物理化学 第 15 页 共 75 页 整个过程所作的功为三步加和。 （3）可逆压缩 如果将蒸发掉的水气慢慢在杯中凝聚，使压力缓 慢增加， 恢复到原状，所作的功为： 1 / 2 ,3 ln 1 2 V V W p dV nRT V V e = − i =  则体系和环境都能恢复到原状。 功与过程小结： 从以上的膨胀与压缩过程看出，功与变化的途径有关。虽然始终态相同，但途径不同，所作的功也 大不相同。显然，可逆膨胀，体系对环境作最大功；可逆压缩，环境对体系作最小功