
5.3金属配合物晶体场理论 2.晶体场理论 设配体带电为-g,配体-金属原子距离为日。在 点电荷模型下,利用经典静电学结果,可得: a 4a3 =-6g+fo。 a 前者为各向同性部分,后者为各向异性部分。 om在0,的对称操作作用下不变 球坐标系下: x4+y4+z4- (ince)() Chapter5多原子分子
2. 晶体场理论 6 Chapter 5 多原子分子 在Oh的对称操作作用下不变 。 设配体带电为 -q ,配体-金属原子距离为 a 。在 点电荷模型下,利用经典静电学结果,可得: 前者为各向同性部分,后者为各向异性部分。 ) 5 3 ( 4 6 35 ˆ 4 4 4 4 5 x y z r a q a q V = − − + + − Voh a q V ˆ 6 ˆ = − + ] 5 3 [(sin cos ) (sin sin ) (cos ) 5 4 4 4 3 4 4 4 4 4 x + y + z − r = r + + − VOh ˆ 球坐标系下: L2 L1 L3 L4 L5 L6 x y z 5.3 金属配合物晶体场理论

5.3金属配合物晶体场理论 2.晶体场理论 单电子薛定谔方程: (h+h)w,=,w, 方=-f=6g+0。 a 用微扰法近似求解单电子薛定谔方程。 电子总波函数: 平a=41.n〉 电子总能量: Ea=∑s 由此可了解配合物的各种性质(稳定性,光谱,磁性.) Chapter5多原子分子
2. 晶体场理论 7 Chapter 5 多原子分子 单电子薛定谔方程: h h i i i + ') = ˆ ˆ ( 0 d = 1 n = i d i 用微扰法近似求解单电子薛定谔方程。 由此可了解配合物的各种性质(稳定性,光谱,磁性.) 电子总波函数: 电子总能量: Voh a q h V ˆ 6 ˆ ' ˆ = − = + 5.3 金属配合物晶体场理论

5.3金属配合物晶体场理论 2.晶体场理论 ()d轨道分裂模式:由晶体场的对称性决定。 对于正八面体场,5个d轨道按0群的不可约表示分类 (查特征标表或相关表) 中心力场 O的不可约表示 d d,2- d 原来简并的d轨道分裂为两组:eg和t2g 8 Chapter5多原子分子
2. 晶体场理论 8 Chapter 5 多原子分子 (ii)d轨道分裂模式:由晶体场的对称性决定。 中心力场 Oh的不可约表示 对于正八面体场,5个d轨道 按Oh群的不可约表示分类 (查特征标表或相关表) 原来简并的 d 轨道分裂为两组:eg 和 t2g。 g z x y g zx yz xy e d d t d d d − 2 2 2 2 5.3 金属配合物晶体场理论
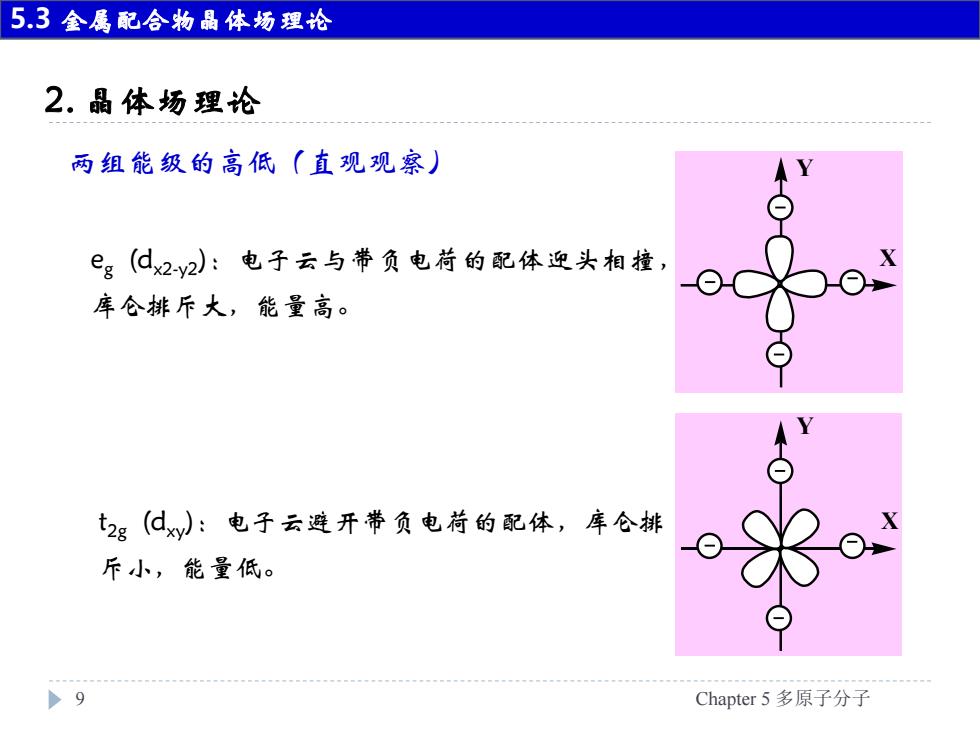
5.3金属配合物晶体场理论 2.晶体场理论 两组能级的高低(直观观察) eg(dx2y2):电子云与带负电荷的配体迎头相撞, 库仑排斥大,能量高。 t2g(dxy):电子云避开带负电荷的配体,库仑排 斥小,能量低。 9 Chapter5多原子分子
2. 晶体场理论 9 Chapter 5 多原子分子 两组能级的高低(直观观察) eg (dx2-y2 ):电子云与带负电荷的配体迎头相撞, 库仑排斥大,能量高。 Y X Y t2g (dxy):电子云避开带负电荷的配体,库仑排 X 斥小,能量低。 5.3 金属配合物晶体场理论