
第三章分析化学中的误差及 数据处理 3.1分析化学中的误差 3.2有效数字及其运算规则 3.3分析化学中的数据处理 3.4显著性检验 3.5可疑值取舍 3.6回归分析法 3.7提高分析结果准确度的方法
1 第三章 分析化学中的误差及 数据处理 3.1 分析化学中的误差 3.2 有效数字及其运算规则 3.3 分析化学中的数据处理 3.4 显著性检验 3.5 可疑值取舍 3.6 回归分析法 3.7 提高分析结果准确度的方法

3.1 分析化学中的误差 3,11 误差与偏差 1、真值(Truth)T(x): 客观存在的真实数值。 (1)理论真值;(绝对真值) (2)计量学约定真值;(规定真值) (3)相对真值。(标准值,如标准试样) 归东理工大军 Analytical Chemistry 2
Analytical Chemistry 2 1、真值(Truth)T(xT): 客观存在的真实数值。 (1)理论真值;(绝对真值) (2)计量学约定真值;(规定真值) (3)相对真值。(标准值,如标准试样) 分析化学中的误差 误差与偏差

2、误差(Error)E: 分析结果(x)和真值之间的差值。 (1)绝对误差(absolute error): E=x-XT (2)相对误差(relative error): E,=E×100%=x-xr×100% E XT XT 相对误差反映误差在真实值中所占的比例。 加东理2大军 Analytical Chemistry 3
Analytical Chemistry 3 2、误差(Error) E: 分析结果(x)和真值之间的差值。 (1)绝对误差(absolute error): E=x-xT (2)相对误差(relative error): 相对误差反映误差在真实值中所占的比例。 100% 100% T T T r − = = x x x x E E
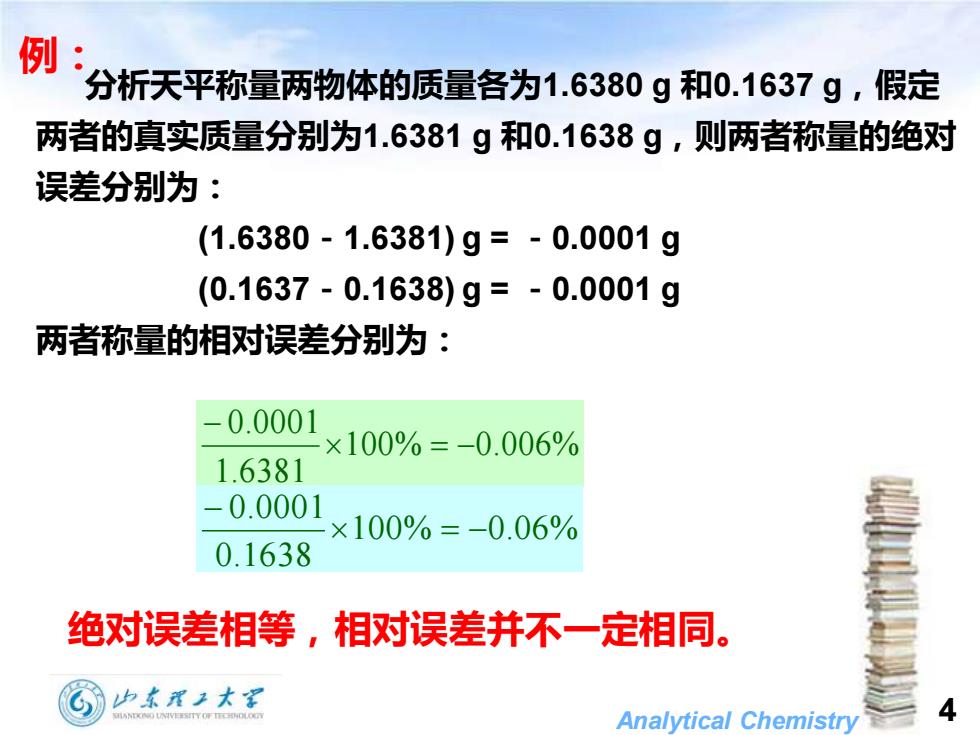
例: 分析天平称量两物体的质量各为1.6380g和0.1637g,假定 两者的真实质量分别为1.6381g和0.1638g,则两者称量的绝对 误差分别为: (1.6380-1.6381)g=-0.0001g (0.1637-0.1638)g=-0.0001g 两者称量的相对误差分别为: 0.0001 ×100%=-0.006% 1.6381 -0.0001 ×100%=-0.06% 0.1638 绝对误差相等,相对误差并不一定相同。 Analytical Chemistry A
Analytical Chemistry 4 例:分析天平称量两物体的质量各为1.6380 g 和0.1637 g,假定 两者的真实质量分别为1.6381 g 和0.1638 g,则两者称量的绝对 误差分别为: (1.6380-1.6381) g = -0.0001 g (0.1637-0.1638) g = -0.0001 g 两者称量的相对误差分别为: 绝对误差相等,相对误差并不一定相同。 100% 0.006% 1.6381 0.0001 = − − 100% 0.06% 0.1638 0.0001 = − −

3、算术平均值: 多次测量结果的平均值。 X1+X2+.+n X二 n 4、中位数: 在由小到大排列的一组测量数值中位于中间的数值。 中位数和算术平均值反映了测量数值的集中趋势。 加东理2大? Analytical Chemistry 5
Analytical Chemistry 5 3、算术平均值: 多次测量结果的平均值。 4、中位数: 在由小到大排列的一组测量数值中位于中间的数值。 中位数和算术平均值反映了测量数值的集中趋势。 n x x x x + + + n = . 1 2