
MTSD@UPC 第一节平动 一维约束体系:限制性运动 ·一维势箱 V(x)= 0, 0<x<L +oo,x<0 or Z>I ·在势箱内部,SEQ同自由粒子相同 ·具有相同通解 吵k(x)=Aei+Beik Location,x 验证与三角函数形式相同 ·势箱外部,由于势能为无穷大,波函数为零(粒子跑不到外面) 吵(x)=0,forx<0orx>L ·与自由粒子波函数有何不同? 2022/3/24 材料化学系:结构化学 6
MTSD@UPC • 一维势箱 • 在势箱内部,SEQ同自由粒子相同 • 具有相同通解 • 势箱外部,由于势能为无穷大,波函数为零(粒子跑不到外面) • 与自由粒子波函数有何不同? 2022/3/24 材料化学系:结构化学 6 第一节 平动 一维约束体系:限制性运动 验证与三角函数形式相同

MTSD@UPC 第一节平动 一维约束体系:考虑波函数约束条件 ·已知波函数具有如下形式 (x)= ∫Aei+Bei, 0<x<L 0, x<0 or >L ·波函数必须连续:引入边界条件 ψk(0)=0,andψk(L)=0 ·允许的波函数及能量具有如下形式: (0)=Csin m7πx n=1,2,… En= n2h2 验证 8mL2, n=1,2,… ·引入边界条件导致能量量子化:约束条件要求波函数具有特定形式, 从而限制了力学量(此处为能量)只能取离散值。 2022/3/24 材料化学系:结构化学 7
MTSD@UPC • 已知波函数具有如下形式 • 波函数必须连续:引入边界条件 • 允许的波函数及能量具有如下形式: • 引入边界条件导致能量量子化:约束条件要求波函数具有特定形式, 从而限制了力学量(此处为能量)只能取离散值。 2022/3/24 材料化学系:结构化学 7 第一节 平动 一维约束体系:考虑波函数约束条件 验证

MTSD@UPC 第一节平动 一维约束体系:归一化 波函数: (0)=Csin 27πc m=1,2,… 代入归一化条件: =c血() -c号-1 故有C=(2/L)12。则一维势箱中波函数的最终形式为: 1/2 0<x<L <0 or x>L 能级为: En= n2h2 8mL2, m=1,2,… 2022/3/24 材料化学系:结构化学 8
MTSD@UPC 波函数: 代入归一化条件: 故有 𝐶 = 2Τ𝐿 1/2。则一维势箱中波函数的最终形式为: 能级为: 2022/3/24 材料化学系:结构化学 8 第一节 平动 一维约束体系:归一化

MTSD@UPC 第一节平动 一维约束体系:讨论 2 1/2 v(x) 0<x<L ·量子数:波函数和能级均依 0 x<0 or x>L 赖于整数no ·一维势箱中,n=1,2, En= n2h2 8mL2, n=1,2,… ·波函数的个数无限 n 100 10 ·无限个能级 Classically allowed energies 81 9 ·能量随n增大而增加 8 ·能级差随n增大而增加 > 3 6 5 6 432 0 2022/3/24 材料化学系:结构化学 9
MTSD@UPC • 量子数:波函数和能级均依 赖于整数 𝑛。 • 一维势箱中,𝑛 = 1, 2, … • 波函数的个数无限 • 无限个能级 • 能量随𝑛增大而增加 • 能级差随𝑛增大而增加 2022/3/24 材料化学系:结构化学 9 第一节 平动 一维约束体系:讨论
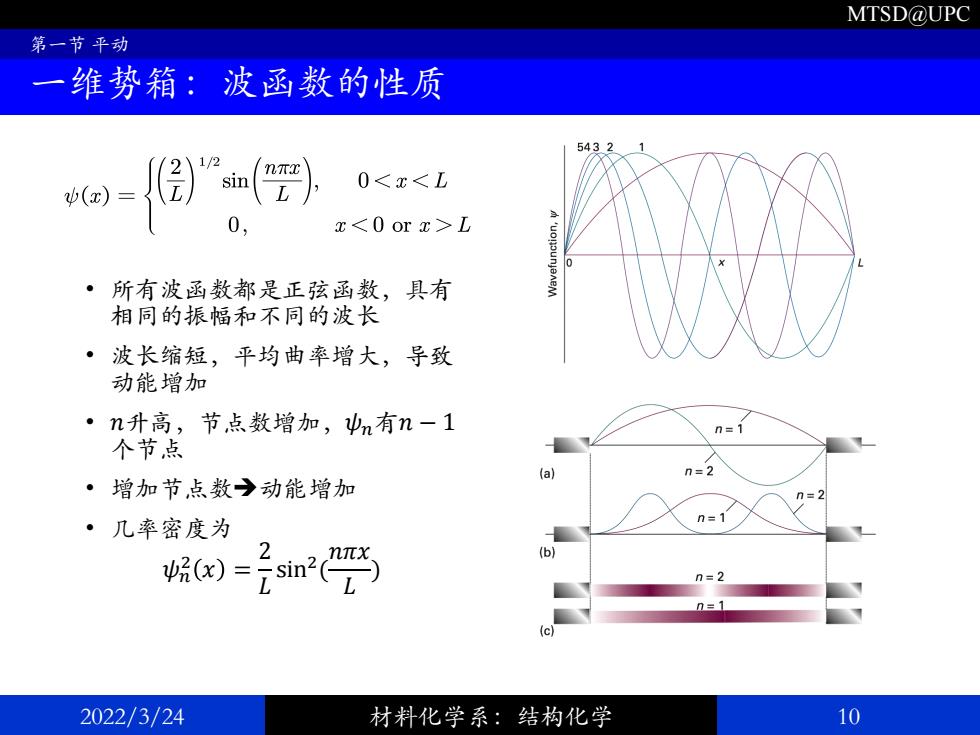
MTSD@UPC 第一节平动 一维势箱:波函数的性质 541 / v(x) sin(nmr) 0<x<L 0, x<0 or I>L ·所有波函数都是正弦函数,具有 相同的振幅和不同的波长 ·波长缩短,平均曲率增大,导致 动能增加 ·n升高,节点数增加,n有n-1 n三 个节点 a】 ·增加节点数→动能增加 n=2 ·几率密度为 呢6e=元sin2 2 6 n=2 2022/3/24 材料化学系:结构化学 10
MTSD@UPC • 所有波函数都是正弦函数,具有 相同的振幅和不同的波长 • 波长缩短,平均曲率增大,导致 动能增加 • 𝑛升高,节点数增加,𝜓𝑛有𝑛 − 1 个节点 • 增加节点数➔动能增加 • 几率密度为 𝜓𝑛 2 𝑥 = 2 𝐿 sin2 ( 𝑛𝜋𝑥 𝐿 ) 2022/3/24 材料化学系:结构化学 10 第一节 平动 一维势箱:波函数的性质