
全程设计 6.2.2 向量的减法运算
6.2.2 向量的减法运算

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导 课前·基础认知 1.相反向量 (1)定义:与向量长度 方向 的向量,叫做a 的相反向量,记作 (2)性质:①a与-a互为 ,(-0)= ②由两个向量和的定义易知+(-)=(-)+=0. ③如果a,b互为相反向量,那么=_,b=-,+b= ④零向量的相反向量仍是
导航 课前·基础认知 1.相反向量 (1)定义:与向量a长度 相等 ,方向 相反 的向量,叫做a 的相反向量,记作 -a . (2)性质:①a与-a互为 相反向量 ,-(-a)= a . ②由两个向量和的定义易知a+(-a)=(-a)+a=0. ③如果a,b互为相反向量,那么a= -b ,b=-a,a+b= 0 . ④零向量的相反向量仍是 零向量
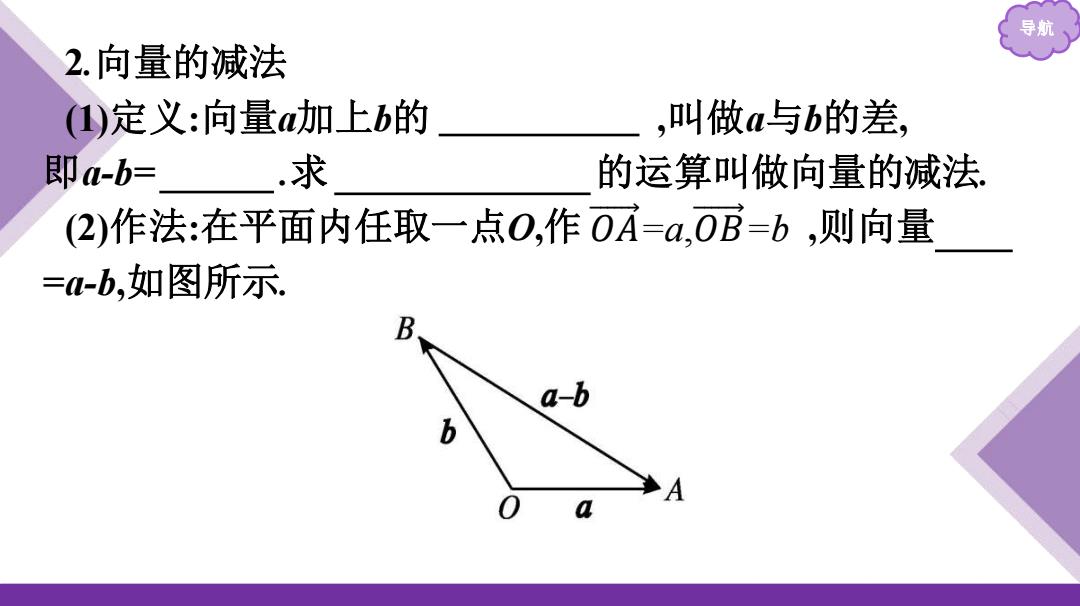
导航 2.向量的减法 ()定义:向量加上b的 ,叫做a与b的差, 即a-b=.求 的运算叫做向量的减法. (2)作法:在平面内任取一点0,作0A=a,0B=b,则向量 =-b,如图所示 a-b b
导航 2.向量的减法 (1)定义:向量a加上b的 相反向量 ,叫做a与b的差, 即a-b= a+(-b) .求 两个向量差 的运算叫做向量的减法. (2)作法:在平面内任取一点O,作 ,则向量 =a-b,如图所示. 𝑂 𝐴 =a,𝑂 𝐵 =b 𝐵 𝐴

导航 微提醒 在用三角形法则作向量减法时,要注意“差向量连接两向 量的终点,箭头指向被减向量”.解题时要结合图形,准确判 断,防止混淆
导航 微提醒 在用三角形法则作向量减法时,要注意“差向量连接两向 量的终点,箭头指向被减向量” .解题时要结合图形,准确判 断,防止混淆