
全程设计 7.2.1 复数的加、减运算及其几何意义
7.2.1 复数的加、减运算及其几何意义

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.复数的加法及其几何意义 (1)复数的加法法则 设z1=a+bi,2=c+(a,b,c,d∈R)是任意两个复数,那么它们的 和(a+bi+(c+)= (2)复数加法的运算律 对任意z1Z23,∈C,有1+2= (亿1+z2)+73=
导航 课前·基础认知 1.复数的加法及其几何意义 (1)复数的加法法则 设z1 =a+bi,z2 =c+di(a,b,c,d∈R)是任意两个复数,那么它们的 和(a+bi)+(c+di)= (a+c)+(b+d)i . (2)复数加法的运算律 对任意z1 ,z2 ,z3∈C,有z1+z2 = z2+z1 , (z1+z2 )+z3 = z1+(z2+z3 )

导航 3)复数加法的几何意义 设0Z,0Z2分别与复数叶bi,c+i对应,则Z= ,0Z2=.由平面向量的坐标运算法则,得 0Z+0Z2= .这说明两个向量0Z与0Z2 的和就是与复数(a+c)+(b+)i对应的向量
导航 (3)复数加法的几何意义 设𝑶𝒁𝟏 ,𝑶𝒁𝟐 分别与复数 a+bi,c+di 对应,则𝑶𝒁𝟏 = (a,b) ,𝑶𝒁𝟐 = (c,d) .由平面向量的坐标运算法则,得 𝑶𝒁𝟏 + 𝑶𝒁𝟐 = (a+c,b+d) .这说明两个向量𝑶𝒁𝟏 与𝑶𝒁𝟐 的和就是与复数(a+c)+(b+d)i 对应的向量
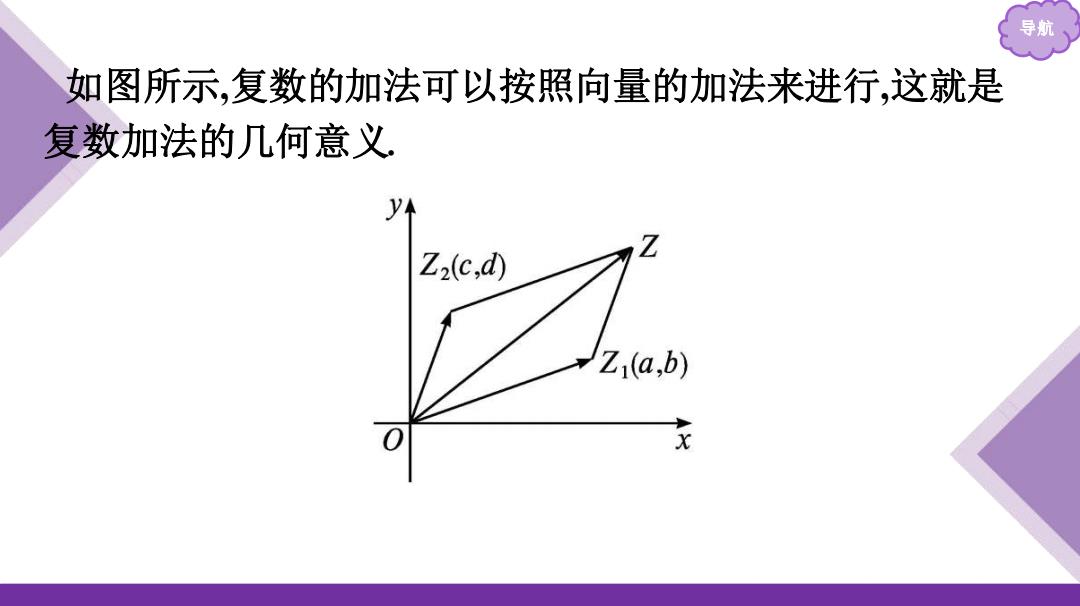
导航 如图所示,复数的加法可以按照向量的加法来进行,这就是 复数加法的几何意义 Z Z2(c,d) Z (a,b)
导航 如图所示,复数的加法可以按照向量的加法来进行,这就是 复数加法的几何意义