-12 第一章几何光学 答案号<s< 作业1.12(教材P372-2.28)直径重=4cm的长玻璃棒的一段磨成曲率半径为R= 2cm的半球形,长为0.1cm的物垂直于棒的轴线,距球面顶.点8cm处.求像的位置 大小并作图. 解由物像关系,得 作业1.12图 +号- R +-1 2 ns' 解得。=12m,因此横向放大率B=一产。=-1,所以成倒立、等大的实像,像的大 小为=-1cm. 答案s=12cm,寸=-1cm. 作业1.13(教材P373-2.30)用作图法求共轭光线】 解红色为光路图,其他颜色为必要的辅助光线. 作业1.13图 作业1.14(教材P373-2.32)透过焦距为9cm的会聚透镜,观察在平静水面下1.2 处的一条小鱼,若透镜位于水面上方0.6m,看到的小鱼位于何处?(假设鱼在透镜光轴 上,natr=1,=4/3) 解由物像关系 m+"=0 授安0
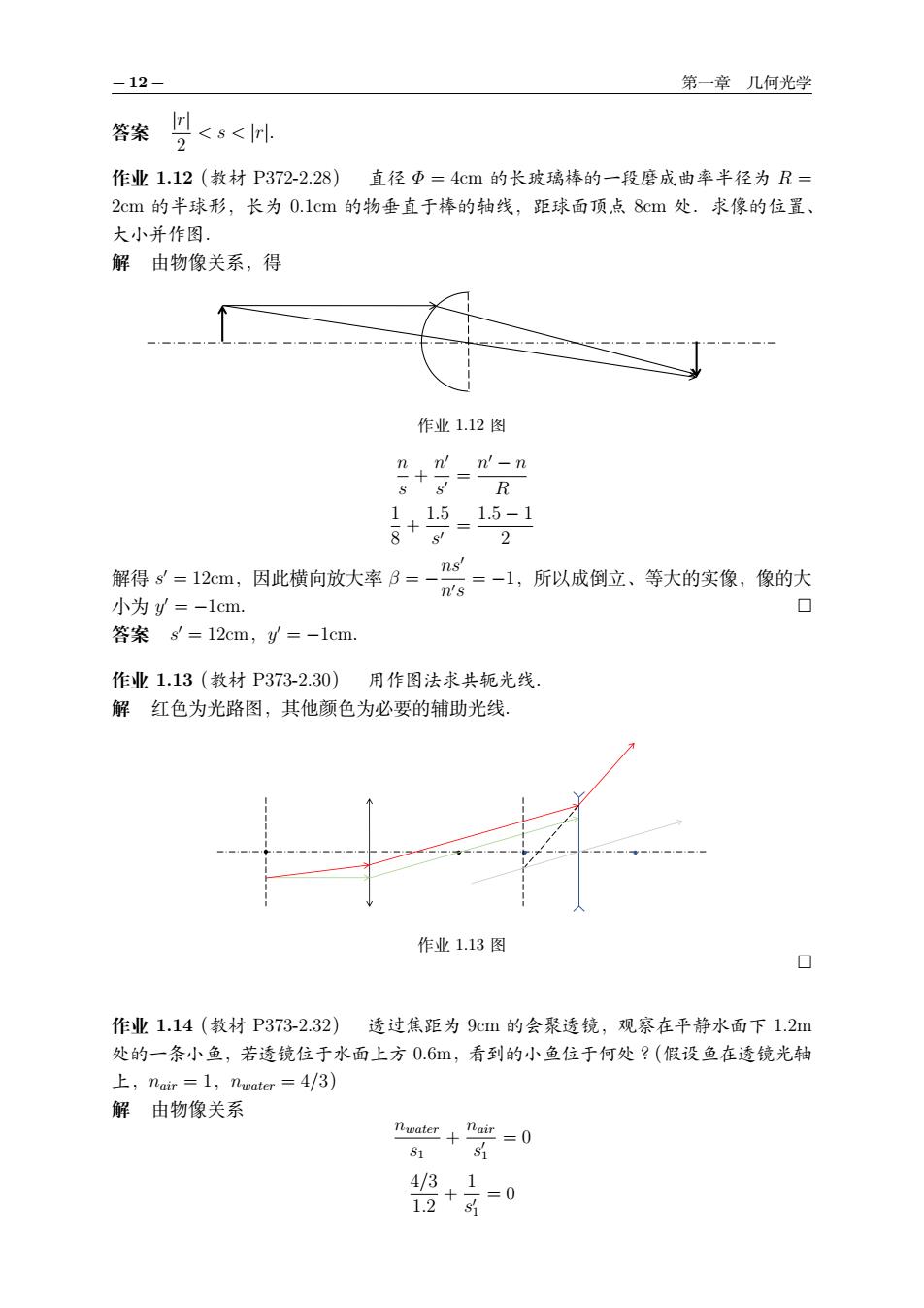
− 12 − 第一章 几何光学 答案 |r| 2 < s < |r|. 作业 1.12(教材 P372-2.28) 直径 Φ = 4cm 的长玻璃棒的一段磨成曲率半径为 R = 2cm 的半球形,长为 0.1cm 的物垂直于棒的轴线,距球面顶点 8cm 处.求像的位置、 大小并作图. 解 由物像关系,得 作业 1.12 图 n s + n ′ s ′ = n ′ − n R 1 8 + 1.5 s ′ = 1.5 − 1 2 解得 s ′ = 12cm,因此横向放大率 β = − ns′ n′s = −1,所以成倒立、等大的实像,像的大 小为 y ′ = −1cm. □ 答案 s ′ = 12cm,y ′ = −1cm. 作业 1.13(教材 P373-2.30) 用作图法求共轭光线. 解 红色为光路图,其他颜色为必要的辅助光线. 作业 1.13 图 □ 作业 1.14(教材 P373-2.32) 透过焦距为 9cm 的会聚透镜,观察在平静水面下 1.2m 处的一条小鱼,若透镜位于水面上方 0.6m,看到的小鱼位于何处?(假设鱼在透镜光轴 上,nair = 1,nwater = 4/3) 解 由物像关系 nwater s1 + nair s ′ 1 = 0 4/3 1.2 + 1 s ′ 1 = 0

光学复习指导 -13- 解得$=-0.9m,因此凸透镜成像的物距s2=0.6+0.9=1.5m. +=7 解得s=1.8m,小鱼仍在原处. 答案号=1.8m,小鱼仍在原处 作业1.15(教材P374-2.36)如图所示的透镜组,物处于最左端透镜的左方10cm处, 是用逐次成像法求最后的成像位置。已知四个薄透镜均处于空气中,像方焦距分别为 f1=f2=-5cm.f0=f=5cm. 解连续使用物像关系,即 1 +=疗 11 + 1 + 1 其中,=10am,解得=-9m,因此=6号+9=10cm,解得号=10m, 因此s3=5-10=-5cm,解得s-oo,因此最后一次成像的像点应在L4得像方焦 点上,即L4右侧5cm处. ▣ 20/3 cm 5cm 10cm L2↓ 作业1.15图 答案最后成像的位置在L4右侧Cm处,即L4的像方焦点上. 作业1.16(教材P374-2.38)如图所示,把曲率半径为r的对称薄双凸透镜放在水平 镜面上,透镜上方为空气,透镜和平面镜之问加入折射率为2的液体,透镜的折射率 为n1·设透镜上方距离l处物像重合,试求n12和r之间的关系 作业1.16图
光学 复 习指 导 − 13 − 解得 s ′ 1 = −0.9m,因此凸透镜成像的物距 s2 = 0.6 + 0.9 = 1.5m. 1 s2 + 1 s ′ 2 = 1 f 解得 s ′ 2 = 1.8m,小鱼仍在原处. □ 答案 s ′ 2 = 1.8m,小鱼仍在原处. 作业 1.15(教材 P374-2.36) 如图所示的透镜组,物处于最左端透镜的左方 10cm 处, 是用逐次成像法求最后的成像位置.已知四个薄透镜均处于空气中,像方焦距分别为 f ′ 1 = f ′ 3 = −5cm,f ′ 2 = f ′ 4 = 5cm. 解 连续使用物像关系,即 1 s1 + 1 s ′ 1 = 1 f ′ 1 1 s2 + 1 s ′ 2 = 1 f ′ 2 1 s3 + 1 s ′ 3 = 1 f ′ 3 1 s4 + 1 s ′ 4 = 1 f ′ 4 其中,s1 = 10cm,解得 s ′ 1 = − 10 3 cm,因此 s2 = 6 2 3 + 10 3 = 10cm,解得 s ′ 2 = 10cm, 因此 s3 = 5 − 10 = −5cm,解得 s ′ 3 = ∞,因此最后一次成像的像点应在 L4 得像方焦 点上,即 L4 右侧 5cm 处. □ L1 L2 L3 L4 20/3 cm 5cm 10cm 作业 1.15 图 答案 最后成像的位置在 L4 右侧 5cm 处,即 L4 的像方焦点上. 作业 1.16(教材 P374-2.38) 如图所示,把曲率半径为 r 的对称薄双凸透镜放在水平 镜面上,透镜上方为空气,透镜和平面镜之间加入折射率为 n2 的液体,透镜的折射率 为 n1.设透镜上方距离 l 处物像重合,试求 n1n2 和 r 之间的关系. 作业 1.16 图

-14 第一章几何光学 解如图所示要想物像重合,光路应满足红线和蓝线, ∫=重 =+=四1+二四 f=l=21-a-1 当然本题也可以用逐次成像的方法分步计算,但是计算量会增大 答案∫=1=201-阳-1
− 14 − 第一章 几何光学 解 如图所示要想物像重合,光路应满足红线和蓝线. f = 1 Φ Φ = Φ1 + Φ2 = n1 − 1 r + n2 − n1 −r f = l = r 2n1 − n2 − 1 当然本题也可以用逐次成像的方法分步计算,但是计算量会增大. □ 答案 f = l = r 2n1 − n2 − 1

第二章 波动光学基础 本章基本要求 1.掌握光波的基本物理量,如频率、波长、波数等。 2.了解定态光波的基本性质和描述方法 3.了解定态光波的复振幅叠加法,熟练掌握振幅和相位的叠加公式. 4.(重点)熟练掌握光的相干条件. 5.了解非定态光波的相关性质. 6.掌握波包和群速度的概念 7.(重难点)熟练掌握光的横波性和光的偏振现象. 8.(重难点)熟练掌握光的五种偏振态的各种性质和判别方法 9.(重难点)熟练掌握起偏和检偏. l0.(重难点)熟练掌握Malus定律,能用Malus定律准确计算偏振光强
第二章 波动光学基础 本章基本要求 1. 掌握光波的基本物理量,如频率、波长、波数等. 2. 了解定态光波的基本性质和描述方法. 3. 了解定态光波的复振幅叠加法,熟练掌握振幅和相位的叠加公式. 4. (重点) 熟练掌握光的相干条件. 5. 了解非定态光波的相关性质. 6. 掌握波包和群速度的概念. 7. (重难点) 熟练掌握光的横波性和光的偏振现象. 8. (重难点) 熟练掌握光的五种偏振态的各种性质和判别方法. 9. (重难点) 熟练掌握起偏和检偏. 10. (重难点) 熟练掌握 Malus 定律,能用 Malus 定律准确计算偏振光强.

-16 第二章波动光学基础 专题2.1光波光波的叠加 ·光的时间周期性和空间周期性 ·光的波动性概念及其关系 ·远场条件、近轴条件和傍轴条件 。波的相位与光程 ·定态光波叠加的振幅和相位 。光的相干条件 ·波包与群速度 例2.1一列波长为的单色波在折射率为n的介质中由A点传播到B点,其相位 改变了2红,则光程改变了多少?从A到B的距离是多少? 提示考虑相位差和光程差、路程之间的关系。 例2.2颜率为6×1014Hz,相速度为3×10m/s的光波,在传搭方向相位差为60 的任意两点之间的最短距离是多少? 例2.3用振幅失量法证明 3cos(kz-wt)+4sin(kz-wt)=5cos(kz-wt+) 并确定9的值 例2.4求两列波 E1=Acos(kz-wt) E2 =-Acos(kz +wt) 叠加后的振动. 提示用三角函数的和差化积公式,但相信大家应该几乎都忘了和差化积是什么,所 以就自己用sin(a士b)和cos(a士b)推导一下,考试真的用到了也是现场推就可以. 例2.5对于光波,证明 -+密 其中,n为介质的折射率,g为群速度
− 16 − 第二章 波动光学基础 专题 2.1 光波 光波的叠加 • 光的时间周期性和空间周期性 • 光的波动性概念及其关系 • 远场条件、近轴条件和傍轴条件 • 波的相位与光程 • 定态光波叠加的振幅和相位 • 光的相干条件 • 波包与群速度 例 2.1 一列波长为 λ0 的单色波在折射率为 n 的介质中由 A 点传播到 B 点,其相位 改变了 2π,则光程改变了多少?从 A 到 B 的距离是多少? 提 示 考虑相位差和光程差、路程之间的关系. 例 2.2 频率为 6 × 1014Hz,相速度为 3 × 108m/s 的光波,在传播方向相位差为 60◦ 的任意两点之间的最短距离是多少? 例 2.3 用振幅矢量法证明 3 cos(kz − ωt) + 4 sin(kz − ωt) = 5 cos(kz − ωt + φ) 并确定 φ 的值. 例 2.4 求两列波 E1 = A cos(kz − ωt) E2 = −A cos(kz + ωt) 叠加后的振动. 提 示 用三角函数的和差化积公式,但相信大家应该几乎都忘了和差化积是什么,所 以就自己用 sin(a ± b) 和 cos(a ± b) 推导一下,考试真的用到了也是现场推就可以. 例 2.5 对于光波,证明 1 νg = n c + ω c · dn dω 其中,n 为介质的折射率,νg 为群速度.