
光学复习指导 -7 water 作业1.2图 sin ia.mar =1,ia.mar =90 又因为na=1,则有 如m=元-高=07 ig.mar arcsin 0.6667 =41.81 ng sin ig =nwe sin iw 假设能发生全反射,加=90°,此时 如=离=080 sin ig=na ig=aresin.8889=62.73>i.mar 即从玻璃射入水的入射角要大于等于62.73°才可以发生全反射,而从水射入玻璃的光 线角度最大只能达到41.81°,因此不能发生全反射 (2)从水射入玻璃 nw sin iw =ng sinig sin ite.mar=1,iu,mar =99 n.e ig.mar =62.739 因为玻璃的临界角为41.81°,ig,mr>icg,故可以发生全反射 答案由空气射入不能发生全反射,由水射入可以发生全反射 ◇ 作业1.3(教材P369-2.3)红光和紫光对同种玻璃的折射率分别是1.51和1.53.当 这些光线射到玻璃和空气的分界面上时,全反射的最小角度是多少?当白光以41°的 角射入到玻璃和空气的界面上时,将会有什么现象发生? 解由临界角计算公式 1 d-aresin 51
光学 复 习指 导 − 7 − 作业 1.2 图 sin ia,max = 1, 即 ia,max = 90◦ 又因为 na = 1,则有 sin ig,max = 1 ng = 1 1.50 = 0.6667 ig,max = arcsin 0.6667 = 41.81◦ ng sin ig = nw sin iw 假设能发生全反射,iw = 90◦,此时 sin ig = nw ng sin iw = 1.33 1.50 = 0.8889 ig = arcsin 0.8889 = 62.73◦ > ig,max 即从玻璃射入水的入射角要大于等于 62.73◦ 才可以发生全反射,而从水射入玻璃的光 线角度最大只能达到 41.81◦,因此不能发生全反射. (2)从水射入玻璃 nw sin iw = ng sin ig sin iw,max = 1, 即 iw,max = 90◦ sin ig,max = nw ng = 1.33 1.50 = 0.8889 ig,max = 62.73◦ 因为玻璃的临界角为 41.81◦,ig,max > iC,g,故可以发生全反射. 答案 由空气射入不能发生全反射,由水射入可以发生全反射. □ 作业 1.3(教材 P369-2.3) 红光和紫光对同种玻璃的折射率分别是 1.51 和 1.53.当 这些光线射到玻璃和空气的分界面上时,全反射的最小角度是多少?当白光以 41◦ 的 角射入到玻璃和空气的界面上时,将会有什么现象发生? 解 由临界角计算公式 1 n = sin iC i Red C = arcsin 1 1.51 = 41.47◦

8 第一章几何光学 必a=acin而=4081 当入射角为i=41°时,由于必emt<i<d,因此玻璃的另一侧能看到一束彩色的 光,这束光由可见光创除临界角小于等于41°部分的光构成,粗略来看这一束光由可见 光抛出紫光剩余部分的复色光组成 答案恐d=41.47°,光ocmt=40.81°,将看到一束彩色光从玻璃的另一侧射出.口 作业1.4(教材P3702.5)证明:当一条光线通过平板玻璃时,出射光线方向不变, 只产生侧向平移.当入射角1很小时,位移△x= n.其中,n为玻璃的折射率, t为玻璃板的厚度, 证明如图所示,作出射光线的反向延长线. 作业1.4图 由折射定律 n sin i =nasin ia 2sin号=n1sin 由于两直线平行,内错角相等,即2=,故1=名,因此出射光线与入射光线平行 只发生侧向平移. 由几何关系,光线在玻璃内通过的光程为d=c2再从第一个折射点向出射光 线反向延长线作垂线,则侧向位移为 △r=dsin(6,-i)=tsin6二边=coi6=t(sin1-cos1tan2) cOS2 cos i2 因为i很小,所以i2也很小,故存在近似sinx≈tanx≈x,cosx≈l,故有 ini≈4=2 sini2 i2 n 血6= 得证 作业1.5(教材P370-2.7)顶角为50°的棱镜的6m=35°,如果浸入水中,最小偏向 角等于多少?水的折射率为1.33
− 8 − 第一章 几何光学 i V iolent C = arcsin 1 1.51 = 40.81◦ 当入射角为 i = 41◦ 时,由于 i V iolent C < i < iRed C ,因此玻璃的另一侧能看到一束彩色的 光,这束光由可见光刨除临界角小于等于 41◦ 部分的光构成,粗略来看这一束光由可见 光抛出紫光剩余部分的复色光组成. 答案 i Red C = 41.47◦,i V iolent C = 40.81◦,将看到一束彩色光从玻璃的另一侧射出. □ 作业 1.4(教材 P370-2.5) 证明:当一条光线通过平板玻璃时,出射光线方向不变, 只产生侧向平移.当入射角 i1 很小时,位移 ∆x = n − 1 n i1t.其中,n 为玻璃的折射率, t 为玻璃板的厚度. 证明 如图所示,作出射光线的反向延长线. 作业 1.4 图 由折射定律 n1 sin i1 = n2 sin i2 n2 sin i ′ 2 = n1 sin i ′ 1 由于两直线平行,内错角相等,即 i2 = i ′ 2,故 i1 = i ′ 1,因此出射光线与入射光线平行, 只发生侧向平移. 由几何关系,光线在玻璃内通过的光程为 d = t cosi2 ,再从第一个折射点向出射光 线反向延长线作垂线,则侧向位移为 ∆x = d sin(i1 − i2) = tsin(i1 − i2) cosi2 = t sin i1 cosi2 − cosi1 sin i2 cosi2 = t(sin i1 − cosi1 tan i2) 因为 i1 很小,所以 i2 也很小,故存在近似 sin x ≈ tan x ≈ x,cos x ≈ 1,故有 sin i1 sin i2 ≈ i1 i2 = n2 n1 sin i2 = sin i1 n ∆x = t(i1 − i1 n ) = n − 1 n i1t 得证. □ 作业 1.5(教材 P370-2.7) 顶角为 50◦ 的棱镜的 δm = 35◦,如果浸入水中,最小偏向 角等于多少?水的折射率为 1.33.
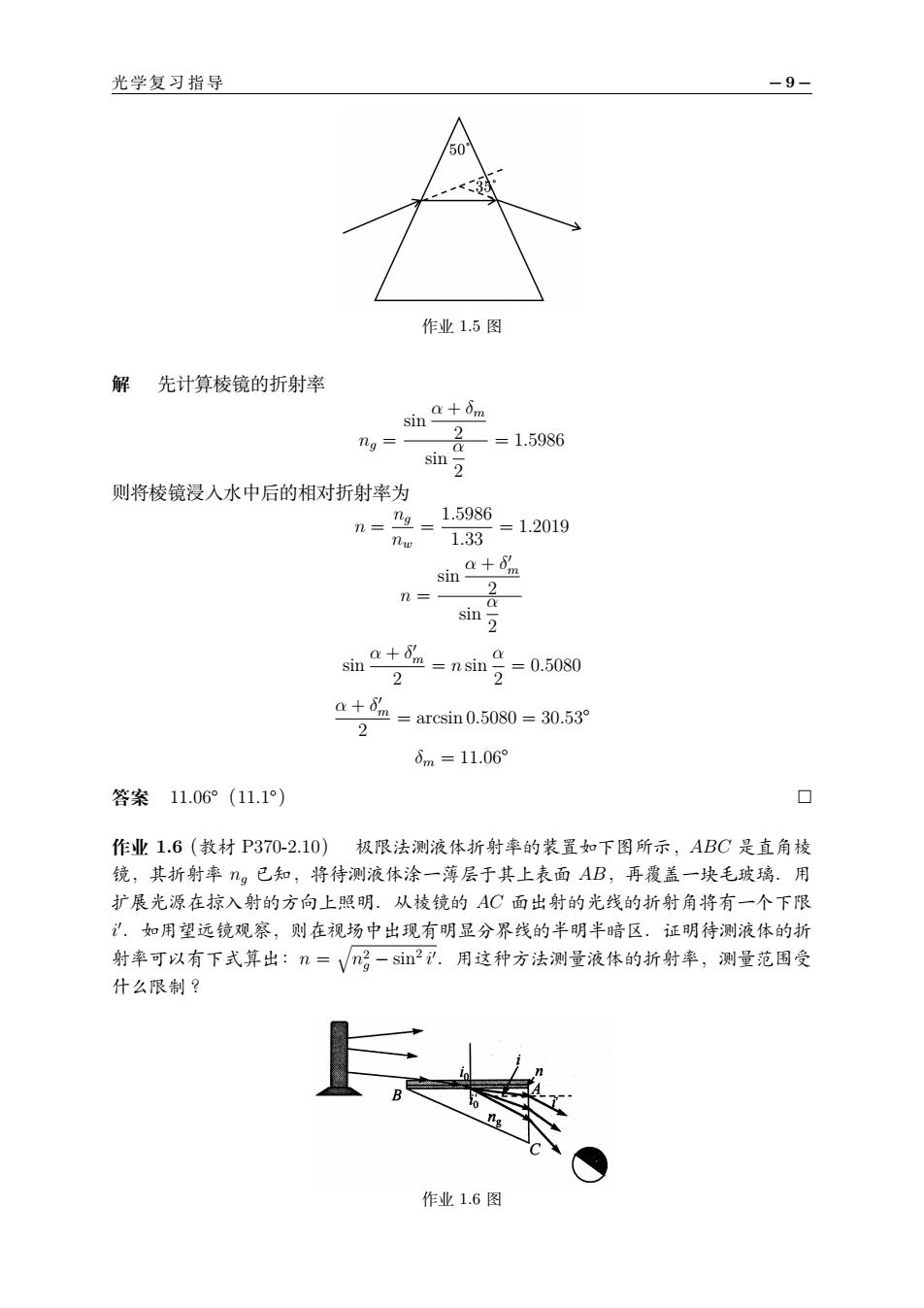
光学复习指导 -9 作业1.5图 解先计算棱镜的折射率 sinom ng= =1.5986 sin 2 则将棱镜浸人水中后的相对折射率为 n-1.5986 1.33-1.2019 ia+ n= n+=nsim号=05080 2 a+%=arcin0.5080=30.53 6m=11.06 答案11.06°(11.1) 作业1.6(教材P370-2.10)极限法测液体折射率的装置如下图所示,ABC是直角棱 镜,其折射率g已知,将待测液体涂一薄层于其上表面AB,再覆盖一块毛玻璃。用 扩展光源在掠入射的方向上照明.从棱镜的AC面出射的光线的折射角将有一个下限 .如用望远镜观察,则在视场中出现有明显分界线的半明半暗区。证明待测液体的折 射率可以有下式算出:n=√n。-si孔.用这种方法测量液体的折射率,测量范围受 什么限制? 作业1.6图
光学 复 习指 导 − 9 − 作业 1.5 图 解 先计算棱镜的折射率 ng = sin α + δm 2 sin α 2 = 1.5986 则将棱镜浸入水中后的相对折射率为 n = ng nw = 1.5986 1.33 = 1.2019 n = sin α + δ ′ m 2 sin α 2 sin α + δ ′ m 2 = n sin α 2 = 0.5080 α + δ ′ m 2 = arcsin 0.5080 = 30.53◦ δm = 11.06◦ 答案 11.06◦(11.1◦) □ 作业 1.6(教材 P370-2.10) 极限法测液体折射率的装置如下图所示,ABC 是直角棱 镜,其折射率 ng 已知,将待测液体涂一薄层于其上表面 AB,再覆盖一块毛玻璃.用 扩展光源在掠入射的方向上照明.从棱镜的 AC 面出射的光线的折射角将有一个下限 i ′.如用望远镜观察,则在视场中出现有明显分界线的半明半暗区.证明待测液体的折 射率可以有下式算出:n = q n2 g − sin2 i ′.用这种方法测量液体的折射率,测量范围受 什么限制? 作业 1.6 图

-10- 第一章几何光学 证明由于是掠入射,可将人射角视为90°,由折射定律 nsin io=ngsini sin=ng cos sin2i=ng cos?io=na(1-sin2 io)=ng-ng sin2io ng-n2 sin2 io 明暗交界处有0=90°,故有 n=Vng sin2 可见,要求液体的折射率n<ng 作业1.7(补充习题)用Fermat定理证明反射定律. A、 B 作业1.7图 证明如图所示,从A点经过C点最后到B点的光程为 (ACB)=nAC+nBC=√候+z子+nV3+x 由Fermat原理要求光程最短,则 (4CB) V保++房+疗nm-n血红=0 sin in =sin i i1=i2 反射定律得证 作业1.8(教材P371-2.15)一玻璃杯,底部为凸球面,球面下嵌一画,空杯看去,与 普通酒杯无异;注入酒后,则底部呈现美丽画面,请解释. 答案未加入酒时,底部为一凸透镜,画在一倍焦距和二倍焦距之间,在很远处形成 正立放大的实像,故看不到画.加入酒后,相当于在底部加上一个凹透镜,形成一个虚 像,同时这个虚像的位置发生改变,成像在距离较近处,所以人能看到画面。 解释这道题有如下要点,首先是形成凸透镜和凹透镜分别成实像和虚像,但是注意, 成实像或者虚像不是观察者能不能看到的关键,关键取决于像的位置在不在观察者视 野范围内,所以除了成像的虚实还要说明未加酒时像的位置观察者看不到,而加了酒观 察者能看到,这样这道题的回答才能落脚到看到与看不到上,否则会答非所问. 作业1.9(教材P371-2.16)一球面反射镜将平行光汇聚在x0=20cm处;将水(折 射率约为43)注满球面,光通过一张白纸片上的针孔射向反射镜,距离x为多少时在 纸片上成清晰的像?
− 10 − 第一章 几何光学 证明 由于是掠入射,可将入射角视为 90◦,由折射定律 n sin i0 = ng sin i ′ 0 sin i ′ = ng cosi ′ 0 sin2 i ′ = n 2 g cos2 i ′ 0 = n 2 g (1 − sin2 i ′ 0 ) = n 2 g − n 2 g sin2 i ′ 0 = n 2 g − n 2 sin2 i0 明暗交界处有 i0 = 90◦,故有 n = q n2 g − sin2 i ′ 可见,要求液体的折射率 n < ng. □ 作业 1.7(补充习题) 用 Fermat 定理证明反射定律. 作业 1.7 图 证明 如图所示,从 A 点经过 C 点最后到 B 点的光程为 (ACB) = nAC + nBC = n q h 2 1 + x 2 1 + n q h 2 2 + x 2 2 由 Fermat 原理要求光程最短,则 d dx(ACB) = nx1 q h 2 1 + x 2 1 + nx2 q h 2 2 + x 2 2 = n sin i1 − n sin i2 = 0 sin i1 = sin i2 i1 = i2 反射定律得证. □ 作业 1.8(教材 P371-2.15) 一玻璃杯,底部为凸球面,球面下嵌一画,空杯看去,与 普通酒杯无异;注入酒后,则底部呈现美丽画面,请解释. 答案 未加入酒时,底部为一凸透镜,画在一倍焦距和二倍焦距之间,在很远处形成 正立放大的实像,故看不到画.加入酒后,相当于在底部加上一个凹透镜,形成一个虚 像,同时这个虚像的位置发生改变,成像在距离较近处,所以人能看到画面. 解释 这道题有如下要点,首先是形成凸透镜和凹透镜分别成实像和虚像,但是注意, 成实像或者虚像不是观察者能不能看到的关键,关键取决于像的位置在不在观察者视 野范围内,所以除了成像的虚实还要说明未加酒时像的位置观察者看不到,而加了酒观 察者能看到,这样这道题的回答才能落脚到看到与看不到上,否则会答非所问. □ 作业 1.9(教材 P371-2.16) 一球面反射镜将平行光汇聚在 x0 = 20cm 处;将水(折 射率约为 4/3)注满球面,光通过一张白纸片上的针孔射向反射镜,距离 x 为多少时在 纸片上成清晰的像?

光学复习指导 -11- 解(方法一)由题意,无水时f=xo=20cm,r=2f=40cm.注水后,有 f=1=15cm 由题意,为了能成清晰的像,物距应等于像距离,故 x=2f'=30cm (方法二)给出一个可行的思路.将整个物理过程分为三部分: STEP1通过水第一次成像; STEP2经过反射镜第二次成像 STEP3通过水第三次成像 列出三次成像的物像方程,根据物距等于像距联立求出x. 答案x=30cm 作业1.10(教材P372-2.25) 一凸面镜浸没在折射率为1.33的水中,高为1cm的物 体在凸面镜40cm处,像在镜后8Cm.求像的大小、正倒、虚实以及凸面镜的曲率半径 和光焦度 解成正立的虚像,由放大率的定义 r- 则像的大小为1×言=0.2cm 由物像关系 解得r=20cm. 由光焦度公式得 =-20-2×13 =-13.3/m 则光焦度为-13.3/m 答案虚像,0.2cm,正立,光焦度-13.3/m 作业1.11(教材P372-2.26)实物放在凹面镜前什么位置能成倒立放大的像?为什 么?是实像还是虚像? 解当实物放在四面镜的左侧时,日=- ,要成倒立放大的像,要求>1,又由物 像关系 +月 1. 因此,-r<s<,同理当实物放在四面镜的右侧时(即放在凹面镜前物距s也是可 以<0的),5<8<r.综上所述,<s< 解释这道题也可以直接带绝对值计算,结果是一样的,但是要注意计算的准确度.口
光学 复 习指 导 − 11 − 解 (方法一)由题意,无水时 f = x0 = 20cm,r = 2f = 40cm.注水后,有 f ′ = f n = 15cm 由题意,为了能成清晰的像,物距应等于像距离,故 x = 2f ′ = 30cm (方法二)给出一个可行的思路.将整个物理过程分为三部分: STEP 1 通过水第一次成像; STEP 2 经过反射镜第二次成像; STEP 3 通过水第三次成像. 列出三次成像的物像方程,根据物距等于像距联立求出 x. □ 答案 x = 30cm 作业 1.10(教材 P372-2.25) 一凸面镜浸没在折射率为 1.33 的水中,高为 1cm 的物 体在凸面镜 40cm 处,像在镜后 8cm.求像的大小、正倒、虚实以及凸面镜的曲率半径 和光焦度. 解 成正立的虚像,由放大率的定义 r = − s ′ s = − −8cm 40cm = 1 5 则像的大小为 1 × 1 5 = 0.2cm. 由物像关系 1 s + 1 s ′ = − 2 r 1 40 − 1 8 = − 2 r 解得 r = 20cm. 由光焦度公式得 Φ = −2n r = − −2 × 1.33 0.2 = −13.3/m 则光焦度为-13.3/m. □ 答案 虚像,0.2cm,正立,光焦度 −13.3/m. 作业 1.11(教材 P372-2.26) 实物放在凹面镜前什么位置能成倒立放大的像?为什 么?是实像还是虚像? 解 当实物放在凹面镜的左侧时,β = − s ′ s ,要成倒立放大的像,要求 |β| > 1,又由物 像关系 1 s ′ + 1 s = − 2 r 因此,−r < s < −r 2 ,同理当实物放在凹面镜的右侧时(即放在凹面镜前物距 s 也是可 以 <0 的),r 2 < s < r.综上所述,|r| 2 < s < |r|. 解释 这道题也可以直接带绝对值计算,结果是一样的,但是要注意计算的准确度.□