
3.薛定谔方程 薛定谔、奥地利物理学家,1926年 建立了以薛定谔方程为基础的波动 力学,1933年获诺贝尔物理学奖。 质点运动、电磁波(光学) 物质波函数满足的规律 牛顿方程、麦克斯韦方程 薛定谔方程
3. 薛定谔方程 薛定谔、奥地利物理学家,1926年 建立了以薛定谔方程为基础的波动 力学,1933年获诺贝尔物理学奖。 质点运动、电磁波(光学) 牛顿方程、麦克斯韦方程 物质波函数满足的规律 薛定谔方程

薛定谔方程的引入 1.单色平面波(德布罗意波) E-hv Acomule Acow 3()co 2( Et =Acos方(Et-xP) i=h/2π b=Ae元(Et-xP) (取实部) 2.薛定谔方程(一维) 从自由粒子平面单色波出发 寻求波函数随时间空间变化的规律
薛定谔方程的引入 1. 单色平面波(德布罗意波) (取实部) 2. 薛定谔方程(一维) 寻求波函数随时间空间变化的规律 从自由粒子平面单色波出发
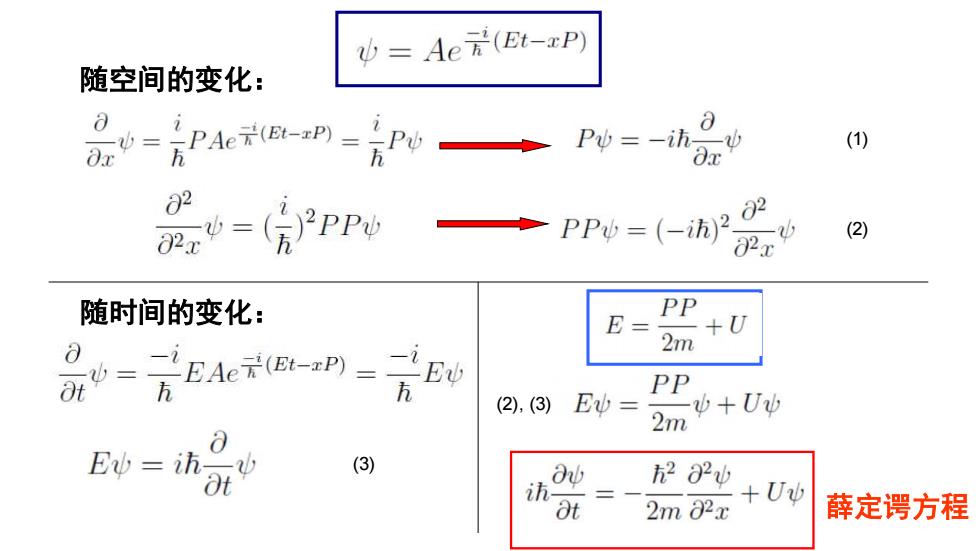
少=Ae元(Et-xP) 随空间的变化: 8 PAe云B=Pv Pw=-一ih证 (1) 02 ◆PP=(-h)2 (2) 随时间的变化: E= PP +U 2m EAe(EL-xP)= (2),(3) E沙= PP ψ+Uψ Ev-ihi (3) Ob 282少 +Uψ 2m 82x 薛定谔方程
随空间的变化: 随时间的变化: (2) (1) (3) 薛定谔方程 (2), (3)

薛定谔方程(三维) h at 2m 72b+Uψ 拉普拉斯算符 V2= 02 802 82 V=ia证 +k 02x 82y 822 4.算符 它= 0 at P=-ihv
薛定谔方程(三维) 拉普拉斯算符 4.算符

连续性方程 ●连续性方程 op+v.J=0 Ot 一一反映了定域的几率守恒 十几率密度 P=Vw≥0 +几率流密度 (yVy-NΨ)
●连续性方程 J 0 t + = ——反映了定域的几率守恒 † 几率密度 * = 0 † 几率流密度 * * ( ) 2 i J m = − − 连续性方程