
随机误差(偶然误差):由某些难以控制且 无法避免的偶然因素造成的误差。 1.特点: (1)不恒定,无法校正,单次误差可大可小,可正可负, 不能确定: (2)服从正态分布规律:大小相近的正误差和负误差 出现的几率机等:小误差出现的频率较高,而大误差 出现的频率较低,很大误差出现的几率近于零。 2.产生的原因: (1)偶然因素(室温,气压的微小变化,仪器的微小变 化,分析人员对各份试样处理时的微小差别等); (2)个人辩别能力(滴定管读数、辨别滴定终点的 颜色) 16 注意:过失误差属于不应有的过失
16 二、 随机误差(偶然误差):由某些难以控制且 无法避免的偶然因素造成的误差。 2.产生的原因: (1)偶然因素(室温,气压的微小变化,仪器的微小变 化,分析人员对各份试样处理时的微小差别等); (2)个人辩别能力(滴定管读数、辨别滴定终点的 颜色) 0 注意: 过失误差属于不应有的过失。 1.特点: (1)不恒定,无法校正,单次误差可大可小,可正可负, 不能确定; (2)服从正态分布规律:大小相近的正误差和负误差 出现的几率机等;小误差出现的频率较高,而大误差 出现的频率较低,很大误差出现的几率近于零
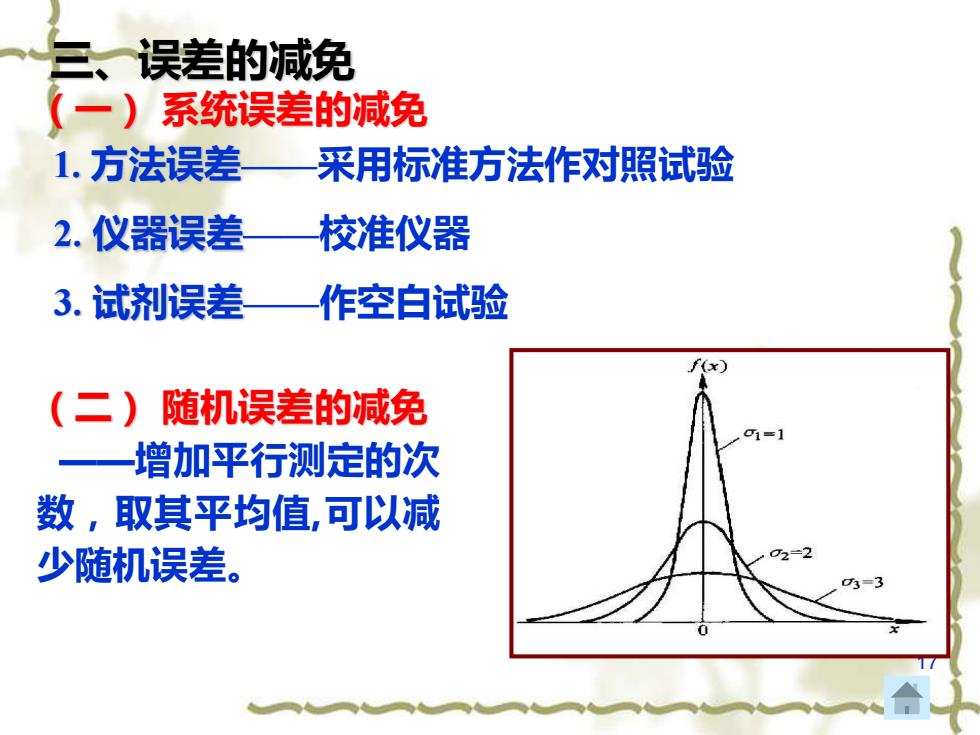
三、误差的减免 (一)系统误差的减免 1.方法误差— 采用标准方法作对照试验 2.仪器误差一 校准仪器 3.试剂误差一 作空白试验 Fx) (二)随机误差的减免 —一增加平行测定的次 数,取其平均值,可以减 少随机误差
17 1. 方法误差——采用标准方法作对照试验 2. 仪器误差——校准仪器 3. 试剂误差——作空白试验 三、误差的减免 (一) 系统误差的减免 (二) 随机误差的减免 ——增加平行测定的次 数,取其平均值,可以减 少随机误差

四、公差 生产部门对于分析结果允许误差的一种表示方法。 含量高,允许公差大;含量低,允许公差小。 超差:超过允许公差,必须重做。 18
18 四、公差 生产部门对于分析结果允许误差的一种表示方法。 含量高,允许公差大;含量低,允许公差小。 超差:超过允许公差,必须重做

3有效数字及其运算规则 一、 有效数字指实际上能测量到的数字。 有效数字=各位确定数字+最后一位可疑数字。 1.实验过程中常遇到两类数字: (1)表示数目(非测量值):如测定次数;倍数;系数;分数 (2)测量值或计算值。数据的位数与测定的准确度有关。 记录的数字不仅表示数量的大小,还要正确地反映 测量的精确程度。 结果绝对误差相对误差有效数字位数 0.32400±0.00001±0.002%5 0.3240±0.0001±0.02% 4 0.324±0.001±0.2% 3 19
19 3 有效数字及其运算规则 一、有效数字:指实际上能测量到的数字。 有效数字 = 各位确定数字 + 最后一位可疑数字。 结果 绝对误差 相对误差 有效数字位数 0.32400 ±0.00001 ±0.002% 5 0.3240 ±0.0001 ±0.02% 4 0.324 ±0.001 ±0.2% 3 1.实验过程中常遇到两类数字: (1)表示数目(非测量值):如测定次数;倍数;系数;分数 (2)测量值或计算值。数据的位数与测定的准确度有关。 记录的数字不仅表示数量的大小,还要正确地反映 测量的精确程度
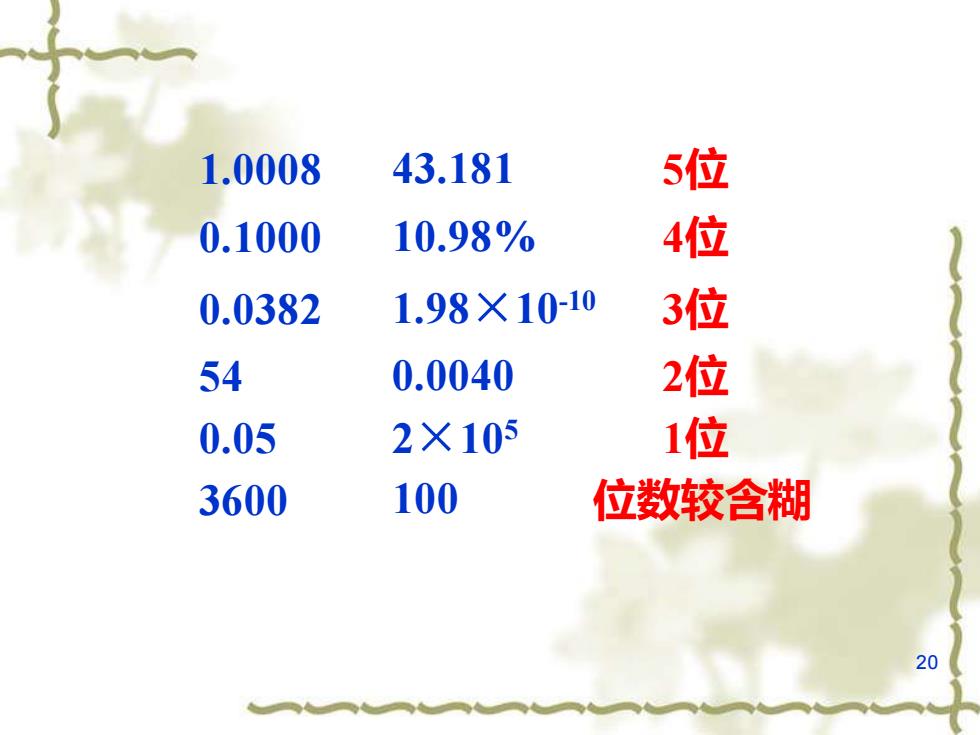
1.0008 43.181 5位 0.1000 10.98% 4位 0.0382 1.98×10-10 3位 54 0.0040 2位 0.05 2×105 1位 3600 100 位数较含糊 20
20 1.0008 43.181 5位 0.1000 10.98% 4位 0.0382 1.98×10-10 3位 54 0.0040 2位 0.05 2×105 1位 3600 100 位数较含糊