
通信原理 第2章随机信号分析 主要内容及要求(以复习方式学习): 1、掌握随机过程及数学特征的定义, 2、熟练掌握平稳随机过程定义、特点; 3、掌握高斯过程的定义、性质, 4、熟悉窄带随机过程的表达式及统计特性 5、熟悉白噪声和带限白噪声的特点; 6、掌握平稳随机过程通过线性系统后特点
通信原理 第2章 随机信号分析 主要内容及要求(以复习方式学习): 1、掌握随机过程及数学特征的定义; 2、熟练掌握平稳随机过程定义、特点; 3、掌握高斯过程的定义、性质; 4、熟悉窄带随机过程的表达式及统计特性 5、熟悉白噪声和带限白噪声的特点; 6、掌握平稳随机过程通过线性系统后特点

通信原理 2.几种常见的概率密度函数 (1)均匀分布 概率密度函数为(x)= b-a a≤x≤b 0 x<0 概率分布函数为F(x)= x-a a≤x≤b b-a x≥a E(x) f(x) 1 b-a x 0 6 (a) (b) 概率分布函数 概率密度函数
通信原理 2.几种常见的概率密度函数 (1)均匀分布 x F(x) 0 a b 0 a b x f (x) 1 b − a 1 (a) (b) 概率分布函数 概率密度函数 a x b b a f x − = 1 概率密度函数为 ( ) − − = x a a x b b a x a x F x 1 0 0 概率分布函数为 ( )
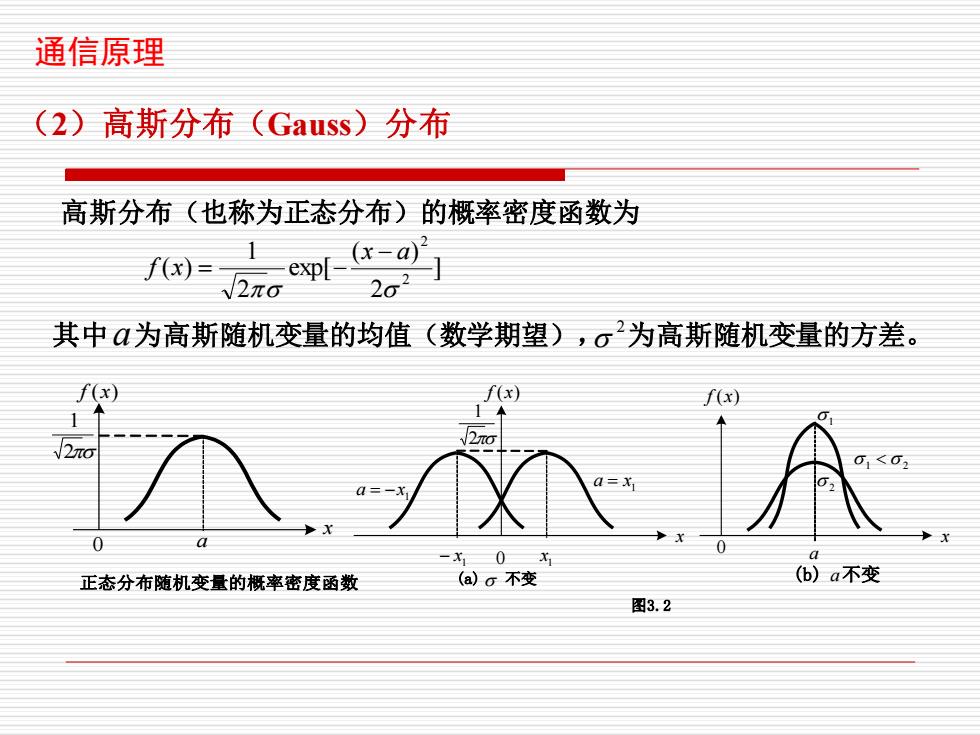
通信原理 (2)高斯分布(Gauss)分布 高斯分布(也称为正态分布)的概率密度函数为 p-a) 2o2 其中a为高斯随机变量的均值(数学期望),6为高斯随机变量的方差。 f(x) f(x) f(x) 1 1◆ N2πo √2πo 01<02 Q=-x a=x 0 a 1 0 -x10X1 正态分布随机变量的概率密度函数 (a)o不变 (b)a不变 图3.2
通信原理 (2)高斯分布(Gauss)分布 高斯分布(也称为正态分布)的概率密度函数为 ] 2 ( ) exp[ 2 1 ( ) 2 2 x a f x − = − 其中 a 为高斯随机变量的均值(数学期望), 2 为高斯随机变量的方差。 x f (x) 0 a 2 1 正态分布随机变量的概率密度函数 x f (x) 0 0 1 a = −x a x f (x) 2 1 (a) 不变 (b) 不变 图3.2 1 − x 1 a = x 1 x 1 2 1 2 a

通信原理 2o2 b-a 其中 eyw 为误差补函数
) 2 ( 2 1 exp( ) 2 . 2 1 ] 2 ( ) exp[ 2 1 ( ) 2 2 2 2 b a z dz erfc dx x a P X b b a b − = − = − = − − 通信原理 erfc x y dy x exp( ) 2 ( ) 2 = − 其中 为误差补函数
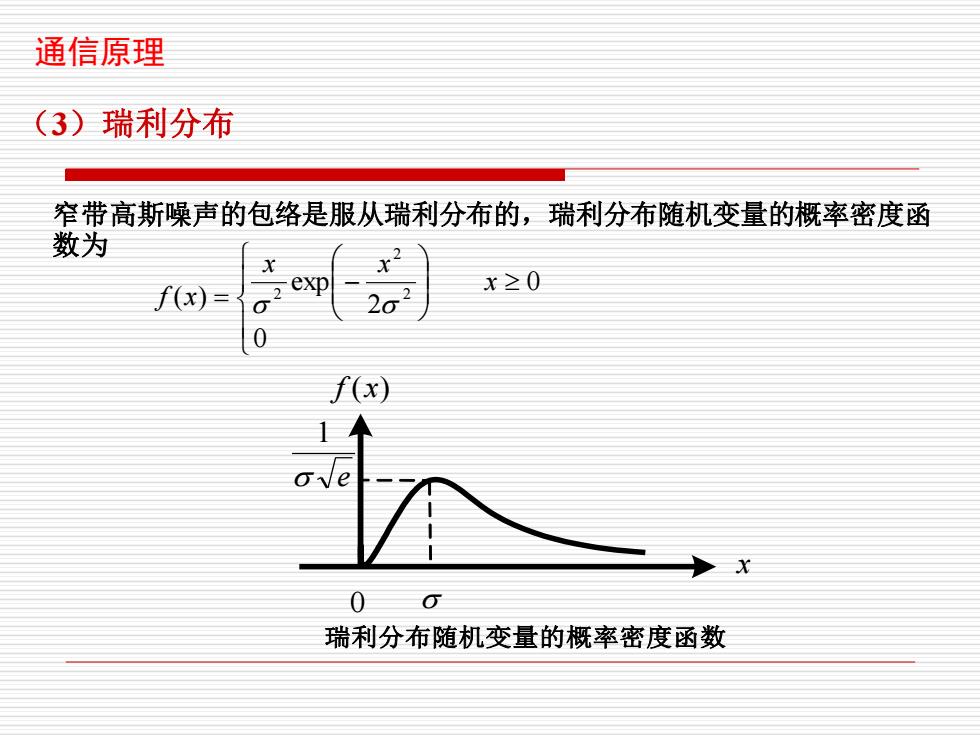
通信原理 (3)瑞利分布 窄带高斯噪声的包络是服从瑞利分布的,瑞利分布随机变量的概率密度函 数为 f(x)= 2exp 202 x≥0 0 f(x) 14 ove 0 瑞利分布随机变量的概率密度函数
通信原理 (3)瑞利分布 窄带高斯噪声的包络是服从瑞利分布的,瑞利分布随机变量的概率密度函 数为 − = 0 0 2 exp ( ) 2 2 2 x x x f x x f (x) 0 e 1 瑞利分布随机变量的概率密度函数