
九=-1 二粒子互换后波函数变号,即 Φ(q1,q2L4,LqL9w,t)=-Φ(41,42,L4L4L4N,t) 反对称波函数 引入 PΦ(i,j》=Φ(j,i)=2Φ(i,j) 粒子 坐标 PD(i,)=PPΦ(i,j》 交换 =2PΦ(i,》=22④(i,j》 算符 所以 九=±1, 对称波函数是P本征值 元=+1的本征态; 反对称波函数是本征值 见=-1的本征态
1 2 1 2 1 q q q t q q q q q i j N q q j i N t = − L L L L L L = − 二粒子互换后波函数变号,即 Φ( , , , ) ( , , , ) Φ 反对称波函数 引入 粒子 坐标 交换 算符 ( , ) ( , ) ˆ ( , ) ˆ ˆ ( , ) ˆ ( , ) ( , ) ( , ) ˆ 2 2 i j i j i j i j i j j i i j i j i j i j i j i j = = = = = 1ˆ 1 ˆ 1 ij ij = = + = − 所以 , 对称波函数是 本征值 的本征态; 反对称波函数是 本征值 的本征态

(三)波函数的对称性不随时间变化 全同粒子体系波函数的这种对称性不随时间变化,即 。初始时刻是对称的,以后时刻永远是对称的; ●初始时刻是反对称的,以后时刻永远是反对称的。 证明:方法1 设全同粒子体系波函数Φ在t时刻是对称的,由体系 哈密顿量是对称的,所以HΦ在t时刻也是对称的。 因为等式两边对称性应是一样的,所以Schrodinger方程 中式左的品0是对称的
全同粒子体系波函数的这种对称性不随时间变化,即 ⚫ 初始时刻是对称的,以后时刻永远是对称的; ⚫ 初始时刻是反对称的,以后时刻永远是反对称的。 证明: 方法 I 设全同粒子体系波函数 s 在 t 时刻是对称的,由体系 哈密顿量是对称的,所以 Hs 在t 时刻也是对称的。 s s s Schrodinger ˆ i H t t = h 因为等式两边对称性应是一样的,所以 方程 中式左的 是对称的。 (三)波函数的对称性不随时间变化
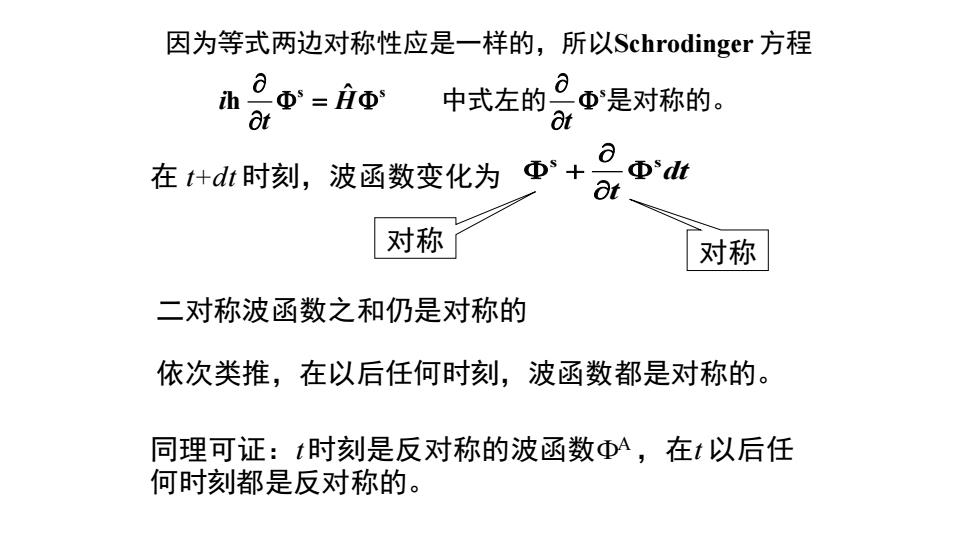
因为等式两边对称性应是一样的,所以Schrodinger方程 8Φ=iw h 中式左的。Φ是对称的。 在t什dt时刻,波函数变化为Φ+ Φdt 对称 对称 二对称波函数之和仍是对称的 依次类推,在以后任何时刻,波函数都是对称的。 同理可证:t时刻是反对称的波函数Φ,在t以后任 何时刻都是反对称的
在 t+dt 时刻,波函数变化为 s sdt t + 对称 对称 二对称波函数之和仍是对称的 依次类推,在以后任何时刻,波函数都是对称的。 同理可证:t时刻是反对称的波函数A,在t 以后任 何时刻都是反对称的。 s s s Schrodinger ˆ i H t t = h 因为等式两边对称性应是一样的,所以 方程 中式左的 是对称的

方法Ⅱ Q[P,A]=0、 .P是守恒量,即 交换对称性不随时间改变。 全同粒子体系哈密顿 量是对称的 结论: 描写全同粒子体系状态的波函数只能是对称的或反对 称的,其对称性不随时间改变。如果体系在某一时刻 处于对称(或反对称)态上,则它将永远处于对称 (或反对称)态上
方法 II ˆ ˆ ˆ Q = ij ij , 0 H 是守恒量,即 交换对称性不随时间改变。 全同粒子体系哈密顿 量是对称的 结论: 描写全同粒子体系状态的波函数只能是对称的或反对 称的,其对称性不随时间改变。如果体系在某一时刻 处于对称(或反对称)态上,则它将永远处于对称 (或反对称)态上

(四)Fermi子和Bose子 实验表明:对于每一种粒子,它们的多粒子波函数 的交换对称性是完全确定的,而且该对称性与粒子 的自旋有确定的联系。 (1)Bose子 凡自旋为整数倍(s=0,1,2,..)的粒子,其 多粒子波函数对于交换2个粒子总是对称的,遵从 Bose统计,故称为Bose子 如:Y光子(s=1);π介子(s=0)
实验表明:对于每一种粒子,它们的多粒子波函数 的交换对称性是完全确定的,而且该对称性与粒子 的自旋有确定的联系。 (1)Bose 子 凡自旋为 整数倍(s = 0,1,2,……) 的粒子,其 多粒子波函数对于交换 2 个粒子总是对称的,遵从 Bose统计,故称为 Bose 子 如: 光子 (s =1); 介子 (s = 0)。 (四)Fermi 子和 Bose 子