
单组分体系的摩尔热力学函数值 ·摩尔体积 H ·摩尔焓 nB ns U'a8 S ·摩尔热力学能 ·摩尔熵 ne ns ·摩尔Helmolz自由能 A nB G ·摩尔Gibbs自由能 G .B np ·这些摩尔热力学函数值都是强度性质
单组分体系的摩尔热力学函数值 • 摩尔体积 * m,B B V V n = • 摩尔焓 • 摩尔热力学能 • 摩尔熵 • 摩尔Helmolz自由能 • 摩尔Gibbs自由能 * m,B B H H n = * m,B B U U n = * m,B B S S n = * m,B B A A n = * m,B B G G n = • 这些摩尔热力学函数值都是强度性质

§4.3 偏摩尔量 偏摩尔量的定义 偏摩尔量的加和公式 *偏摩尔量的求法 Gibbs-Duhem公式- 系统中偏摩尔量之间的关系
§4.3 偏摩尔量 偏摩尔量的定义 Gibbs-Duhem公式—— 系统中偏摩尔量之间的关系 偏摩尔量的加和公式 *偏摩尔量的求法

§4.3 偏摩尔量 多组分系统与单组分系统的差别 单组分系统的广度性质具有加和性 若1mol单组分B物质的体积为 则2mol单组分B物质的体积为 2× VB 而1mol单组分B物质和1mol单组分C物质混合, 得到的混合体积可能有两种情况: ()V=lmol×s+lmol×Vc 形成了混合物 (2)V≠1mol×VmB+1mol×Vmc 形成了溶液
§4.3 偏摩尔量 单组分系统的广度性质具有加和性 * 若 Vm,B 1 mol单组分B物质的体积为 * 则2 mol单组分B物质的体积为 2 Vm,B 而1 mol单组分B物质和1 mol单组分C物质混合, 得到的混合体积可能有两种情况: * * m,B m,C (1) 1 mol 1 mol V V V = + * * m,B m,C (2) 1 mol 1 mol V + V V 形成了混合物 形成了溶液 多组分系统与单组分系统的差别
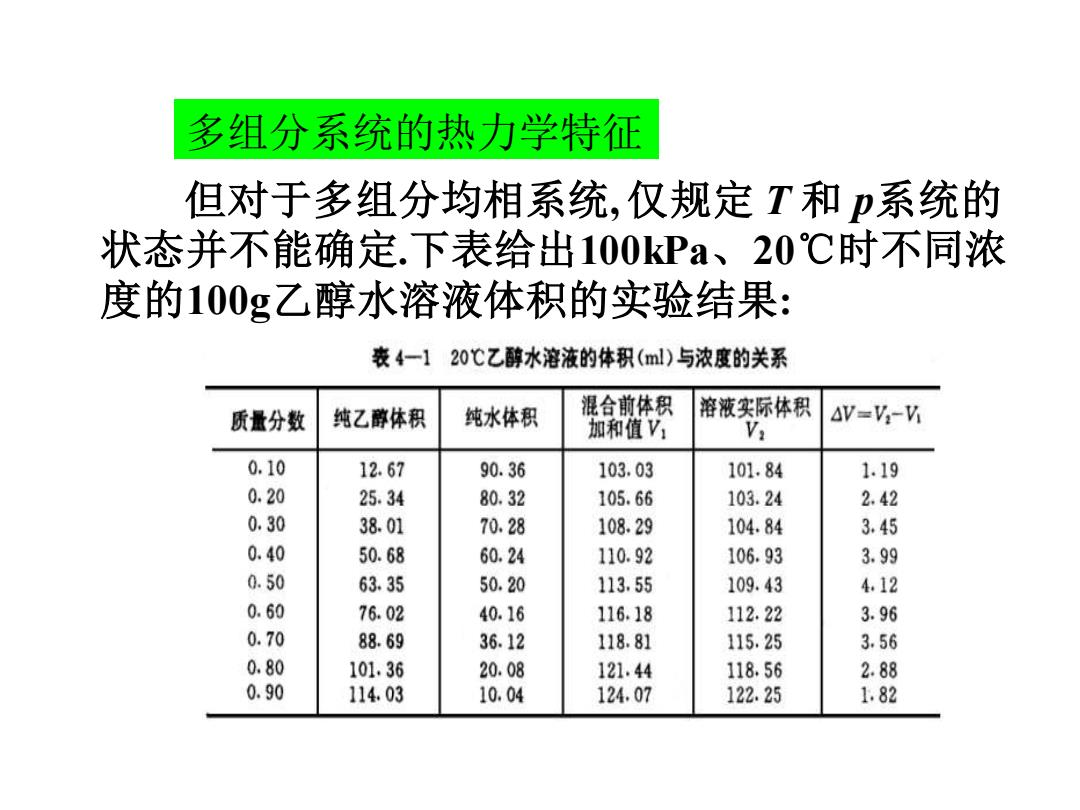
多组分系统的热力学特征 但对于多组分均相系统,仅规定T和p系统的 状态并不能确定.下表给出100kPa、20℃时不同浓 度的100g乙醇水溶液体积的实验结果: 表4一120℃乙醇水溶液的体积(ml)与浓度的关系 质量分数 纯乙醇体积 纯水体积 混合前体积 溶液实际体积 △V=V2-V 加和值V Vi 0.10 12.67 90.36 103.03 101.84 1.19 0.20 25.34 80.32 105.66 103.24 2.42 0.30 38.01 70.28 108.29 104.84 3.45 0.40 50.68 60.24 110.92 106.93 3.99 0.50 63.35 50.20 113.55 109.43 4,12 0.60 76.02 40.16 116.18 112.22 3.96 0.70 88.69 36.12 118.81 115.25 3.56 0.80 101.36 20.08 121.44 118.56 2.88 0.90 114.03 10.04 124.07 122.25 1.82
多组分系统的热力学特征 但对于多组分均相系统, 仅规定 T 和 p系统的 状态并不能确定.下表给出100kPa、20℃时不同浓 度的100g乙醇水溶液体积的实验结果:

从实验数据看,溶液的体积并不等于各组分纯 态体积之和,且体积改变随溶液浓度不同而异.虽然 乙醇和水的m、T、p固定,还必须规定系统中每种 物质的量方可确定系统的状态.因而得出如下结论: ①多组分系统的热力学性质与各种物质的量不 具有简单的加和性. ②多组分系统任一容量性质: z=z(T、p、n1、n2…) 为此我们引入偏摩尔数量的概念
为此我们引入偏摩尔数量的概念. ② 多组分系统任一容量性质: ① 多组分系统的热力学性质与各种物质的量不 具有简单的加和性. 从实验数据看, 溶液的体积并不等于各组分纯 态体积之和, 且体积改变随溶液浓度不同而异. 虽然 乙醇和水的 m、T、p 固定, 还必须规定系统中每种 物质的量方可确定系统的状态. 因而得出如下结论: z = z (T、p、n1、n2 ……)