
5.2对均值和方差的解释 资产回报率的计算 无风险资产 风险资产 《金融经济学二 0.5 ”100(状态a) 0.5 ·120(状态a) 90 80 0.5 .100(状态b) 0.5 80 (状态b) 五讲》 当前价格 未来支付 当前价格 未来支付 (0期) (1期) (0期) (1期) 配套课件 ◆事前回报率(期望回报率)与事后回报率 一风险资产:事前事后回报率不一定相等 E0)=0.5×120+0.5×80 1=25% 120 Ta= 80 80-1=0% 80 -1=50%,%= 一无风险资产:事前事后回报率相等 0.5×100+05x100-1=ra=rm=90 100 E() -1≈11% 90 风险溢价(risk premium)是风险资产的期望回报率超出无风险资产期 望回报率的部分,是对风险资产持有者承担风险的补偿
《 金 融 经 济 学 二 十 五 讲 》 配 套 课 件 5.2 对均值和方差的解释 资产回报率的计算 ◆ 事前回报率(期望回报率)与事后回报率 – 风险资产:事前事后回报率不一定相等 – 无风险资产:事前事后回报率相等 ◆ 风险溢价(risk premium)是风险资产的期望回报率超出无风险资产期 望回报率的部分,是对风险资产持有者承担风险的补偿 6 无风险资产 风险资产 0.5 100 (状态a ) 0.5 120 (状态a ) 90 80 0.5 100 (状态b ) 0.5 80 (状态b ) 当前价格 未来支付 当前价格 未来支付 (0期) (1期) (0期) (1期) 0.5 120 0.5 80 120 80 ( ) 1 25% 1 50%, 1 0% 80 80 80 E r r r a b + = − = = − = = − = 0.5 100 0.5 100 100 ( ) 1 1 11% 90 90 E r r r f fa fb + = − = = = −
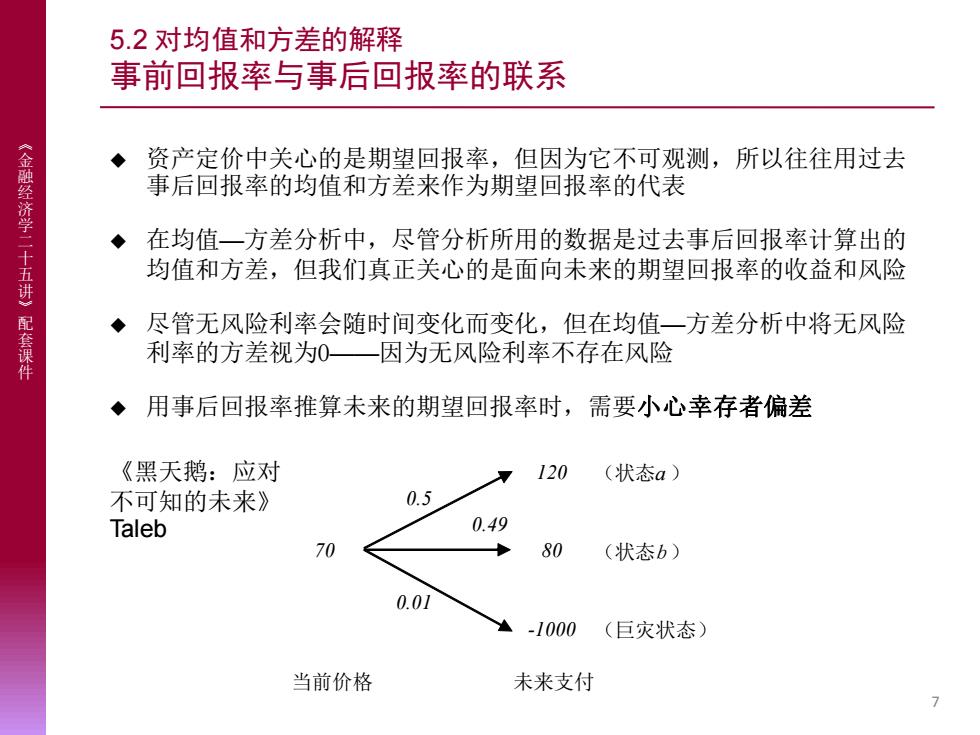
5.2对均值和方差的解释 事前回报率与事后回报率的联系 资产定价中关心的是期望回报率,但因为它不可观测,所以往往用过去 《金融经济学二十 事后回报率的均值和方差来作为期望回报率的代表 ◆在均值一方差分析中,尽管分析所用的数据是过去事后回报率计算出的 讲》 均值和方差,但我们真正关心的是面向未来的期望回报率的收益和风险 ◆尽管无风险利率会随时间变化而变化,但在均值一方差分析中将无风险 套课件 利率的方差视为0—因为无风险利率不存在风险 用事后回报率推算未来的期望回报率时,需要小心幸存者偏差 《黑天鹅:应对 120 (状态a) 不可知的未来》 0.5 Taleb 0.49 70 80 (状态b) 0.01 -1000 (巨灾状态) 当前价格 未来支付 7
《 金 融 经 济 学 二 十 五 讲 》 配 套 课 件 5.2 对均值和方差的解释 事前回报率与事后回报率的联系 ◆ 资产定价中关心的是期望回报率,但因为它不可观测,所以往往用过去 事后回报率的均值和方差来作为期望回报率的代表 ◆ 在均值—方差分析中,尽管分析所用的数据是过去事后回报率计算出的 均值和方差,但我们真正关心的是面向未来的期望回报率的收益和风险 ◆ 尽管无风险利率会随时间变化而变化,但在均值—方差分析中将无风险 利率的方差视为0——因为无风险利率不存在风险 ◆ 用事后回报率推算未来的期望回报率时,需要小心幸存者偏差 7 120 (状态a ) 0.5 0.49 70 80 (状态b ) 0.01 -1000 (巨灾状态) 当前价格 未来支付 《黑天鹅:应对 不可知的未来》 Taleb

5.2对均值和方差的解释 均值、方差和标准差的数学描述 《金融经济学二十 ◆均值 讲》 ◆ 方差 -2-r时 配套课件 ■ 标准差 ◆ 协方差 i=1 相关系数 Ox 00y 8
《 金 融 经 济 学 二 十 五 讲 》 配 套 课 件 5.2 对均值和方差的解释 均值、方差和标准差的数学描述 ◆ 均值 ◆ 方差 ◆ 标准差 ◆ 协方差 ◆ 相关系数 8 1 1 N i i r r N = = 2 2 1 1 ( ) N r i i r r N = = − 2 1 1 ( ) N r i i r r N = = − 1 1 ( )( ) N xy i i i x x y y N = = − − xy xy x y =

5.3资产组合的均值方差特性 种无风险资产和一种风险资产的组合 ◆ 资产组合(portfolio):由多种资产组合起来的一个资产集合 《金融经济学二 - 记为w1,w2,w小,其中的w,是财富分配在第种资产上的比例,且∑w,=1 一可以做多、做空或不持有某种资产(w,可正可负也可为0) ◆一种无风险资产和一种风险资产的组合 五讲》 -无风险资产r,风险资产r,(均值与标准差为r,与o,) 配套课件 一组合的均值和方差 万。=E(I-w)r,+wr=(I-w)r,+w7=,+w叵-5) o2=E[-wy+wr,-(1-wy-7]=E[w2(,-E)2]=wo 一在均值一标准差平面上组合画出 Er。 一条直线 万,=+ T.-ILo Os 9
《 金 融 经 济 学 二 十 五 讲 》 配 套 课 件 5.3 资产组合的均值方差特性 一种无风险资产和一种风险资产的组合 ◆ 资产组合(portfolio):由多种资产组合起来的一个资产集合 – 记为 (w1 , w2 , ., wn ),其中的wi是财富分配在第i种资产上的比例,且∑iwi=1 – 可以做多、做空或不持有某种资产(wi可正可负也可为0) ◆ 一种无风险资产和一种风险资产的组合 – 无风险资产rf,风险资产rs(均值与标准差为͞rs与σs) – 组合的均值和方差 9 2 2 2 2 2 2 (1 ) (1 ) ( ) (1 ) (1 ) ( ) p f s f s f s f p f s f s s s s r E w r wr w r wr r w r r E w r wr w r wr E w r r w = − + = − + = + − = − + − − − = − = s f p f p s r r r r − = + E ( r p ) s rf σ p 0 – 在均值—标准差平面上组合画出 一条直线
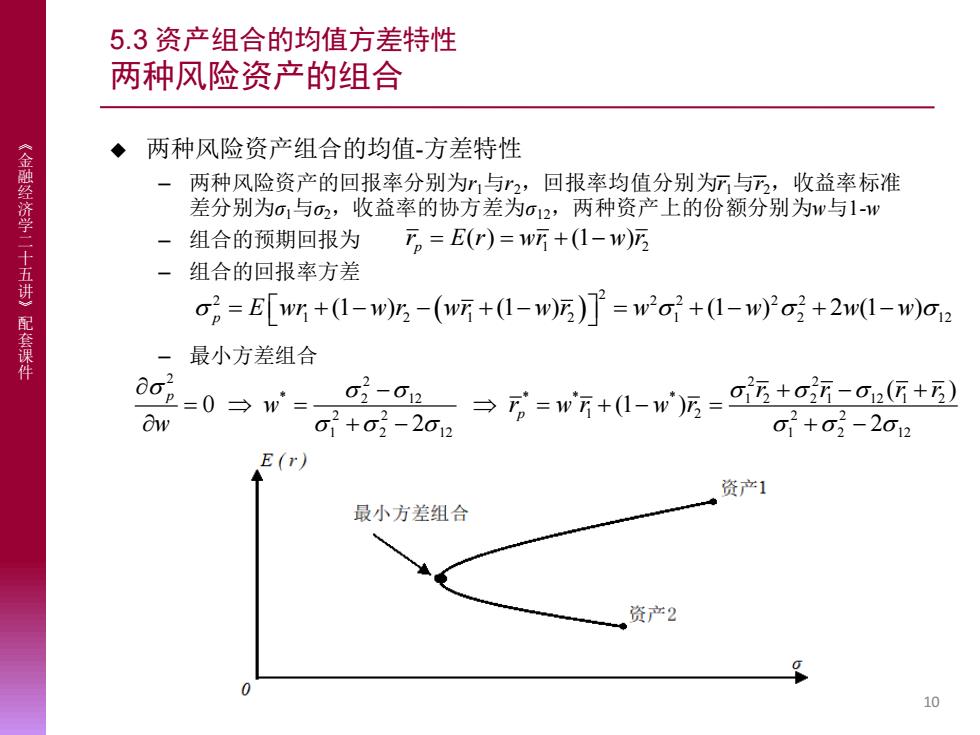
5.3资产组合的均值方差特性 两种风险资产的组合 ◆两种风险资产组合的均值-方差特性 《金融经济学二十 - 两种风险资产的回报率分别为与2,回报率均值分别为7与2,收益率标准 差分别为o1与2,收益率的协方差为o12,两种资产上的份额分别为w与1-w 一组合的预期回报为 万,=E(r)=w听+(1-w)万 讲》 一组合的回报率方差 o2=E[wr+(1-w)5-(听+(1-w))了=w2o2+1-w)2o+2w1-wm)o12 配套课件 最小方差组合 ao-0→w= a二0;。→方=w方+1-w万=西+oG+ Ow 6+o1-2012 01+0-2012 E(r》 资产1 最小方差组合 资产2 10
《 金 融 经 济 学 二 十 五 讲 》 配 套 课 件 5.3 资产组合的均值方差特性 两种风险资产的组合 ◆ 两种风险资产组合的均值-方差特性 – 两种风险资产的回报率分别为r1与r2,回报率均值分别为͞r1与͞r2,收益率标准 差分别为σ1与σ2,收益率的协方差为σ12,两种资产上的份额分别为w与1-w – 组合的预期回报为 – 组合的回报率方差 – 最小方差组合 10 1 2 ( ) (1 ) p r E r wr w r = = + − ( ) 2 2 2 2 2 2 1 2 1 2 1 2 12 (1 ) (1 ) (1 ) 2 (1 ) p = + − − + − = + − + − E wr w r wr w r w w w w 2 2 2 2 * * * * 2 12 1 2 2 1 12 1 2 2 2 2 2 1 2 1 2 12 1 2 12 ( ) 0 (1 ) 2 2 p p r r r r w r w r w r w − + − + = = = + − = + − + −