
无套利定价 期权定价 第一部分:欧式期权定价 1
无套利定价 期权定价 第一部分:欧式期权定价 1

欧式期权 ·假设x是资产在t=1的支付,S是资产在t=0的价值。 定义(欧式期权) An European call(put)option on the stock with strike price K and maturity date t is a security that gives the buyer the right to buy (sell)the stock at maturity at price K. 课堂练习:根据上面的信息,在草稿本上写出欧式看涨和看跌期权 的oayoff;并且画出payoff的图。 2
欧式期权 • 假设෩X是资产在t=1的支付,S是资产在t=0的价值。 定义(欧式期权) 课堂练习:根据上面的信息,在草稿本上写出欧式看涨和看跌期权 的payoff;并且画出payoff的图。 An European call (put) option on the stock with strike price K and maturity date t is a security that gives the buyer the right to buy (sell) the stock at maturity at price K . 2
美式期权 定义(美式期权)An American call(put)option on the stock with strike price K and maturity date t is a security that gives the buyer the right to buy(sell)the stock at any time before and including the maturity date at price K. 一 些符号: 符号 含义 c(S.K) 欧式看涨期权在t=0的价值 C(S,9 美式看涨期权在t=0的价值 p(S.K) 欧式看跌期权在t=0的价值 P(S,9 美式看跌期权在t=0的价值 3
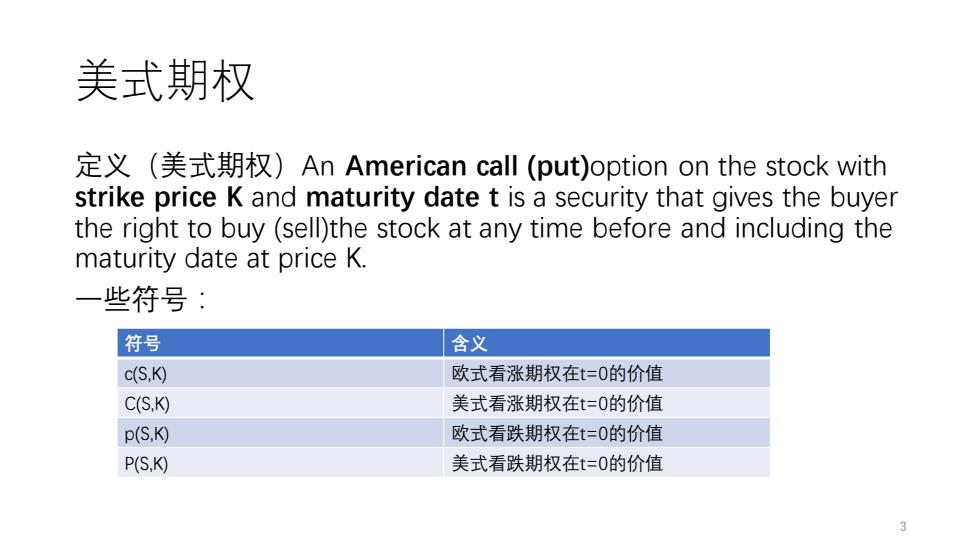
美式期权 定义(美式期权)An American call (put)option on the stock with strike price K and maturity date t is a security that gives the buyer the right to buy (sell)the stock at any time before and including the maturity date at price K. 一些符号: 符号 含义 c(S,K) 欧式看涨期权在t=0的价值 C(S,K) 美式看涨期权在t=0的价值 p(S,K) 欧式看跌期权在t=0的价值 P(S,K) 美式看跌期权在t=0的价值 3

欧式期权价值的无套利性质 ·根据无套利定价原理,对于两个资产A和B,X4w≥XBw),那么 S4≥SB使用无套利定价理论,期权价值满足如下的关系。 定理1c(S,K)和p(S,K)是非负的; =8-M20,=K-0420 定理2c(S,K)对于K是非递增的,p(S,K)对K是非递减的; Proof::K>K2,max[0,X-K≤max[0,产-K].Thus,c(S,K)≤c(S,K2)
欧式期权价值的无套利性质 • 根据无套利定价原理,对于两个资产A和B,𝑋𝐴 𝑤 ≥ 𝑋𝐵 𝑤 , 那么 𝑆𝐴 ≥ 𝑆𝐵.使用无套利定价理论,期权价值满足如下的关系。 定理1 𝑐 𝑆,𝐾 和𝑝 𝑆,𝐾 是非负的; 定理2 𝑐 𝑆,𝐾 对于K是非递增的,𝑝 𝑆,𝐾 对K是非递减的; 4

定理3c(S,K)和p(S,K)对于K是凸(Convex)的; Proof::K1>K2和a∈(0,1), max0,X-aK+a-aK=maxf0,a(区-K)+a-a(&-K] <amax(1-a)max0, 换句话说,max本身是一个凸函数。 定理4令0≥0为N个资产的投资份额,则 c(S0,KT0)≤∑0:c(S,K),p(sr8,KT0)≤∑0:~pS,K) 即投资组合期权的价值小于期权投资组合价值的总和。 经济学含义:大盘指数期权比个股期权比例加总便宜 5
定理3 𝑐 𝑆,𝐾 和 𝑝 𝑆,𝐾 对于K是凸(Convex)的; Proof: ∀𝐾1 > 𝐾2和𝛼 ∈ (0,1), 换句话说,max本身是一个凸函数。 定理4 令𝜃 ≥ 0 为N个资产的投资份额,则 即投资组合期权的价值小于期权投资组合价值的总和。 经济学含义:大盘指数期权比个股期权比例加总便宜 5