
《金融经济学二十五讲》配套课件 第8讲期望效用理论 ©0③可 EY以CsA■ 本作品采用知识共享署名非商业性使用-相同方式共享4.0国际许可协议进行许可
《 金 融 经 济 学 二 十 五 讲 》 配 套 课 件 《金融经济学二十五讲》配套课件 第8讲 期望效用理论 本作品采用知识共享署名-非商业性使用-相同方式共享4.0 国际许可协议进行许可
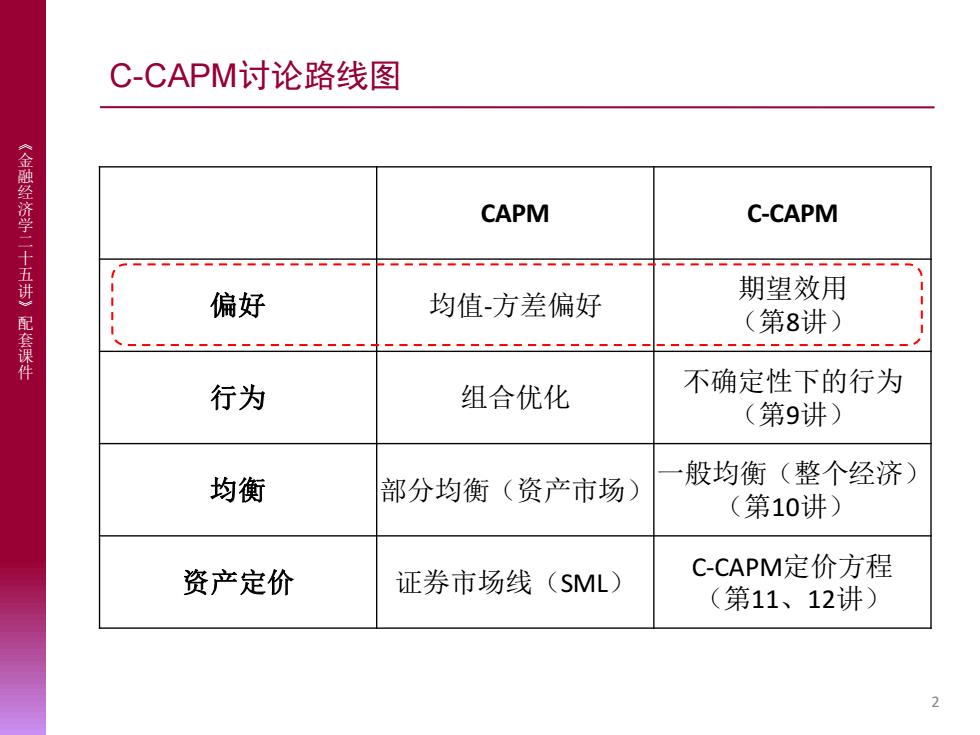
C-CAPM讨论路线图 《金融经济学二十五讲》 CAPM C-CAPM 偏好 均值方差偏好 期望效用 配套课件 (第8讲) 行为 组合优化 不确定性下的行为 (第9讲) 均衡 部分均衡(资产市场) 般均衡(整个经济) (第10讲) 资产定价 证券市场线(SML) C-CAPM定价方程 (第11、12讲) 2
《 金 融 经 济 学 二 十 五 讲 》 配 套 课 件 C-CAPM讨论路线图 CAPM C-CAPM 偏好 均值-方差偏好 期望效用 (第8讲) 行为 组合优化 不确定性下的行为 (第9讲) 均衡 部分均衡(资产市场)一般均衡(整个经济) (第10讲) 资产定价 证券市场线(SML) C-CAPM定价方程 (第11、12讲) 2

8.1从CAPM到一般均衡定价 《金融经济学二 ◆CAPM理论存在的不足 -偏好上的不足 五讲》 ·均值一方差偏好并非完备的偏好 ·仅使用回报率的均值和方差来做判断,丢失了更高阶矩的信息 配套课件 一分析方法上存在的不足 ·CAPM是一个部分均衡的静态模型—因而无法对资产价格的决定问题 做更为深入的分析(比如无法回答市场组合的回报率的决定问题) ◆从CAPM到一般均衡定价的理论拓展 一偏好上:风险下的偏好理论体系一期望效用理论 一均衡分析上:从部分均衡到一般均衡
《 金 融 经 济 学 二 十 五 讲 》 配 套 课 件 8.1 从CAPM到一般均衡定价 ◆ CAPM理论存在的不足 – 偏好上的不足 • 均值—方差偏好并非完备的偏好 • 仅使用回报率的均值和方差来做判断,丢失了更高阶矩的信息 – 分析方法上存在的不足 • CAPM是一个部分均衡的静态模型——因而无法对资产价格的决定问题 做更为深入的分析(比如无法回答市场组合的回报率的决定问题) ◆ 从CAPM到一般均衡定价的理论拓展 – 偏好上:风险下的偏好理论体系——期望效用理论 – 均衡分析上:从部分均衡到一般均衡 3

8.2风险状况下的选择理论—期望效用 引子:圣彼得堡悖论 《金融经济学二 ◆圣彼得堡悖论(St.Petersburg Paradox) -抛一个公平的硬币(正面与反面出现的概率各为1/2) 一连续抛掷硬币,直到第一次抛出正面后赌局结束 -如果第n次才第一次抛出正面,参与者可以得到的奖励是2l元钱 五讲》 一这一赌局给参与者带来的期望收益是无穷大,但甚至很难找到愿意掏10元钱 配套课件 来参加这一赌局的人 期收益=1+侣×2+得×4+-2r2=2r= ◆ 丹尼尔伯努利对圣彼得堡悖论的解释: 假设人们的效用是对数效用,那么人们只愿意掏2元钱参加这一赌局 期望效用=∑()”1n(2)=ln2∑()”·(n-) n=】 }+g+6+. =ln2. ++6+宽. +6+立+☆. =ln2(3++g+6+.)=n2<∞ +克+高+
《 金 融 经 济 学 二 十 五 讲 》 配 套 课 件 8.2 风险状况下的选择理论——期望效用 引子:圣彼得堡悖论 ◆ 圣彼得堡悖论(St. Petersburg Paradox) – 抛一个公平的硬币(正面与反面出现的概率各为1/2) – 连续抛掷硬币,直到第一次抛出正面后赌局结束 – 如果第n次才第一次抛出正面,参与者可以得到的奖励是2 n-1元钱 – 这一赌局给参与者带来的期望收益是无穷大,但甚至很难找到愿意掏10元钱 来参加这一赌局的人 ◆ 丹尼尔•伯努利对圣彼得堡悖论的解释: – 假设人们的效用是对数效用,那么人们只愿意掏2元钱参加这一赌局 4 ( ) 2 3 1 1 1 2 2 1 1 1 1 1 1 2 4 2 1 2 2 2 n n n n t − = = = + + + = = = 期望收益 ( ) ( ) ( ) 1 1 1 2 2 1 1 1 1 1 4 8 16 1 1 1 8 16 32 1 1 1 1 1 1 1 2 4 8 16 16 32 64 1 1 1 32 64 128 ln(2 ) ln 2 ( 1) ln 2 ln 2 ln 2 n n n n n n − = = = = − + + + + + + = = + + + + = + + + + + + 期望效用

8.2风险状况下的选择理论—期望效用 偏好与效用函数 《金融经济学二十 ◆ 理性(rational)偏好(定义8.I):在选择空间中的一种偏好被称为理性 的,如果它满足完备性与传递性 讲》 -完备性(complete):商品空间中任意两个元素之间都可以用这种偏好来做比 较 配套课件 -传递性(transitive):x不差于y,y也不差于z,那么x不差于z ◆连续(continuous)偏好(定义8.2):一种偏好关系如果在极限下也能保 留,就被称为连续的 命题81:如果一个偏好是理性且连续的,那么它可以用一个连续函数 u)来表示
《 金 融 经 济 学 二 十 五 讲 》 配 套 课 件 8.2 风险状况下的选择理论——期望效用 偏好与效用函数 ◆ 理性(rational)偏好(定义8.1):在选择空间中的一种偏好被称为理性 的,如果它满足完备性与传递性 – 完备性(complete):商品空间中任意两个元素之间都可以用这种偏好来做比 较 – 传递性(transitive):x不差于y,y也不差于z,那么x不差于z ◆ 连续(continuous)偏好(定义8.2):一种偏好关系如果在极限下也能保 留,就被称为连续的 ◆ 命题8.1:如果一个偏好是理性且连续的,那么它可以用一个连续函数 u(x)来表示 5