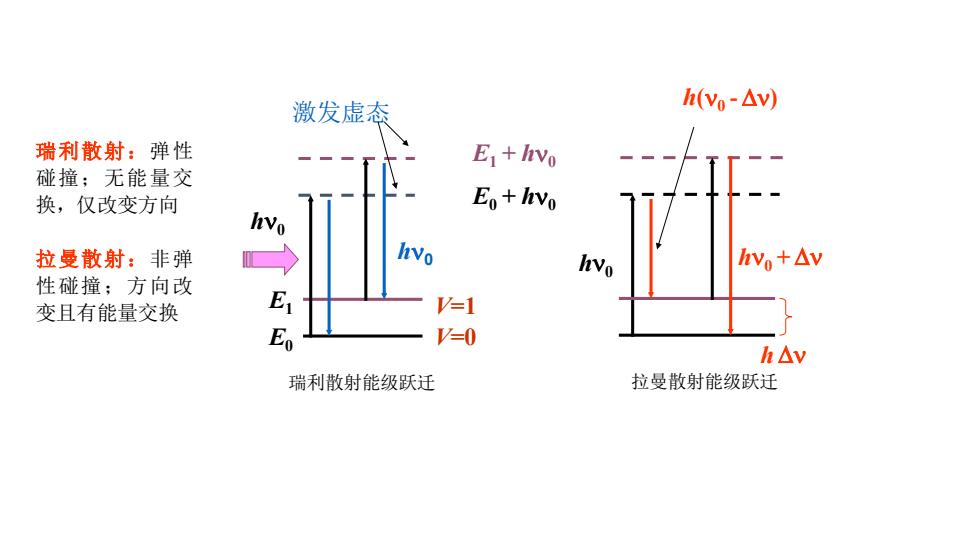
激发虚态 h(vo-△v) 瑞利散射:弹性 E+hvo 碰撞;无能量交 换,仅改变方向 Eo+lvo 拉曼散射:非弹 hvo hvo hvo+△v 性碰撞;方向改 变且有能量交换 V=1 E V=0 h△v 瑞利散射能级跃迁 拉曼散射能级跃迁
瑞利散射:弹性 碰撞;无能量交 换,仅改变方向 拉曼散射:非弹 性碰撞;方向改 变且有能量交换 瑞利散射能级跃迁 拉曼散射能级跃迁 h E0 E1 V=1 V=0 h0 h0 h0 h0 + E1 + h0 E0 + h0 h(0 - ) 激发虚态
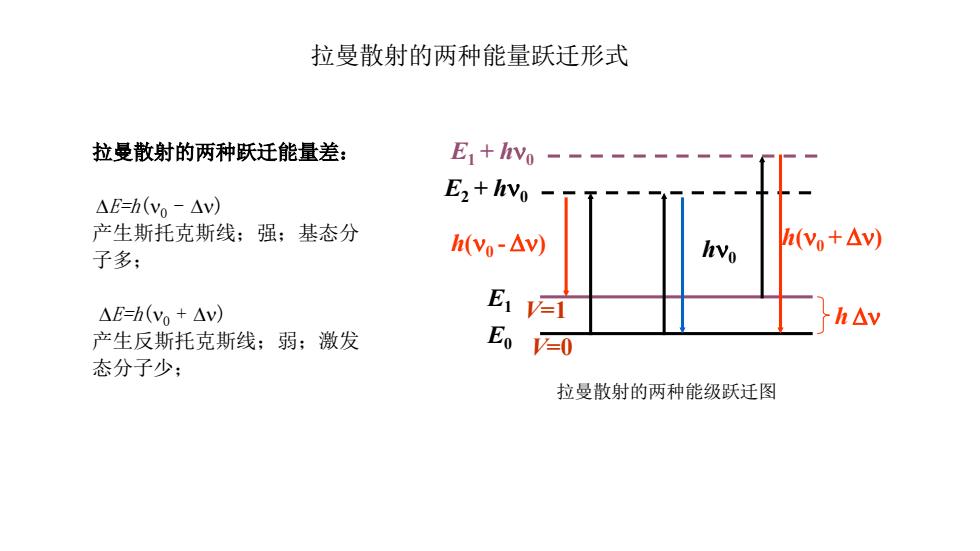
拉曼散射的两种能量跃迁形式 拉曼散射的两种跃迁能量差: E+- E2+hvo- △E=h(vo-△v) 产生斯托克斯线;强;基态分 h(Vo-△v) h(Vo+△v) 子多: hvo △E=h(Vo+△v) E11 h△y 产生反斯托克斯线;弱;激发 Eo =0 态分子少: 拉曼散射的两种能级跃迁图
拉曼散射的两种跃迁能量差: E=h(0 - ) 产生斯托克斯线;强;基态分 子多; E=h(0 + ) 产生反斯托克斯线;弱;激发 态分子少; h(0 + ) E0 E1 V=1 V=0 E1 + h0 E2 + h0 h h0 h(0 - ) 拉曼散射的两种能量跃迁形式 拉曼散射的两种能级跃迁图

机理研究 一个分子的总能量E可认为是内在能量E。、平动能E平、振动能E振、 转动能E转、以及分子内电子运动能量E电子的总和 E=E。+E平+E振+E转十E电子 式中, E。-分子的固有内能 E平-分子的平动能 E振一分子内部原子在其平衡位置附近的振动能 E转一分子绕其重心的转动能 E电子一分子内部价电子的运动能量
机理研究 • 一个分子的总能量 E可认为是内在能量 E0、平动能 E平、振动能 E振、 转动能 E转、以及分子内电子运动能量 E电子的总和 E = E0 + E平 + E振 + E转 + E电子 式中, E0 –分子的固有内能 E平 – 分子的平动能 E振 – 分子内部原子在其平衡位置附近的振动能 E转 – 分子绕其重心的转动能 E电子 – 分子内部价电子的运动能量

机理研究 分子吸收外界能量后,就能引起分子能级的跃迁,即从基态跃迁到 激发态 分子吸收能量具有量子化特征,即分子只能吸收等于两个能级之差 的能量 △E=E2-E,=hv=hcn 。 E是固有内能、不随运动而改变:E平是连续变化的,不会量子化, 因此,E和E平的改变不会产生光谱 。 一个分子吸收外来辐射的能量后,其能量变化△E为其振动能变化 △E振、转动能变化△E转、以及分子内电子运动能量变化△E电子的总 和 △E=△E振+AE转+△E电子 其中 振动能级间隔△E振:一般在0.05~leV 转动能级间隔△E转:一般小于0.05eV,甚至可小至104eV以下 价电子能级间隔△E电子:相对最大,一般1~20eV
机理研究 • 分子吸收外界能量后,就能引起分子能级的跃迁,即从基态跃迁到 激发态 • 分子吸收能量具有量子化特征,即分子只能吸收等于两个能级之差 的能量 ∆E = E2 – E1 = hv = hc/λ • E0是固有内能、不随运动而改变;E平是连续变化的,不会量子化, 因此,E0和E平的改变不会产生光谱 • 一个分子吸收外来辐射的能量后,其能量变化 ∆E为其振动能变化 ∆E振、转动能变化 ∆E转、以及分子内电子运动能量变化 ∆E电子的总 和 E = E振 + E转 + E电子 其中 振动能级间隔 ∆E振:一般在0.05 ~ 1eV 转动能级间隔 ∆E转:一般小于0.05 eV,甚至可小至10-4 eV以下 价电子能级间隔 ∆E电子:相对最大,一般1 ~ 20 eV

机理研究 ·转动能级间隔△E转: 一般小于0.05eV,甚至可小至104eV以下 跃迁产生吸收光谱位于远红外区 。振动能级间隔△E振: 一般在0.05~1eV 跃迁产生的吸收光谱位于红外区 ·价电子能级间隔△E电子: 一般1~20eV 跃迁产生的吸收光谱位于紫外区与可见区
机理研究 • 转动能级间隔 ∆E转: 一般小于0.05 eV,甚至可小至10-4 eV以下 跃迁产生吸收光谱位于远红外区 • 振动能级间隔 ∆E振: 一般在0.05 ~ 1eV 跃迁产生的吸收光谱位于红外区 • 价电子能级间隔 ∆E电子: 一般1 ~ 20 eV 跃迁产生的吸收光谱位于紫外区与可见区