
2

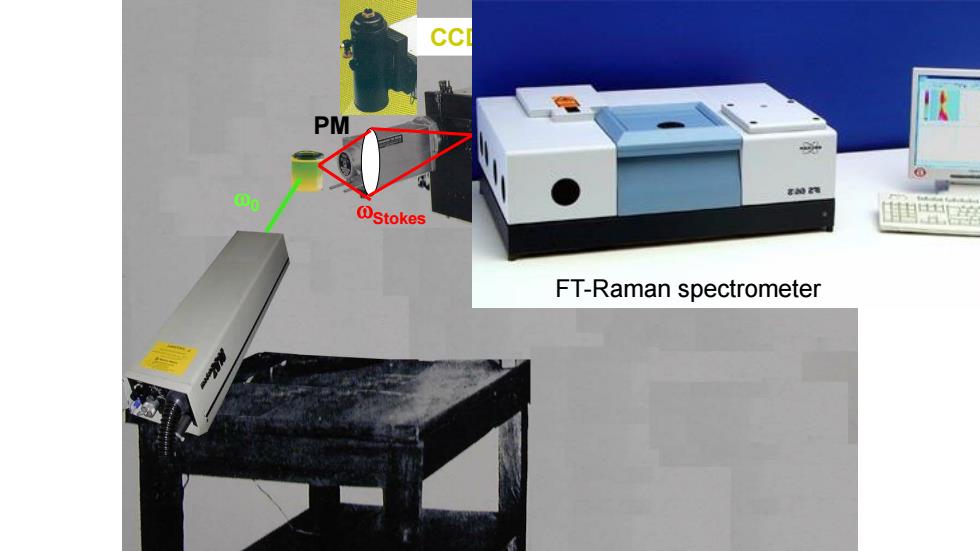
CCI PM 00 @stokes FT-Raman spectrometer
w0 wStokes CCD-Camera PM FT-Raman spectrometer

·光是一种电磁波,具有波粒二象性 光量子(即光子)的能量与电磁辐射的频率有关,其数学表达式为: E=hv 式中, E-辐射的光量子的能量,J h-普朗克常数,6.63*1034J·s v-辐射的光量子的频率,Hz 若用波长表示,则光子的能量与其波长的关系的数学表达式为: E=hy=hc/λ 式中, E,h,v,同上 c-光速,3*108m/s 入-辐射的光量子的波长,m
• 光是一种电磁波,具有波粒二象性 • 光量子(即光子)的能量与电磁辐射的频率有关,其数学表达式为: 式中, E – 辐射的光量子的能量, J h – 普朗克常数,6.63*10-34 J · s v – 辐射的光量子的频率, Hz E = h • 若用波长表示,则光子的能量与其波长的关系的数学表达式为: E = h = hc / 式中, E,h,v,同上 c – 光速,3*108 m/s λ – 辐射的光量子的波长, m

1.拉曼光谱原理 ◆光是电磁辐射,其作用于物质,光子与物质分子发生碰撞时,产生散射光。 ◆当一束频率为V,的单色光照射到样品上后,分子可以使入射光发生散射。大部分光只是改变方向发 生散射,而光的频率仍与激发光的频率相同,弹性碰撞,这种散射称为瑞利散射。 ◆约占总散射光强度的106~1010的散射,不仅改变了光的传播方向,而且散射光的频率也改变了, 不同于激发光的频率,非弹性碰撞,称为拉曼散射。 ◆拉曼散射中频率减少的称为斯托克斯散射,频率增加的散射称为反斯托克斯散射,斯托克斯散射 通常要比反斯托克斯散射强得多,拉曼光谱仪通常测定的大多是斯托克斯散射,也统称为拉曼散 射。 ◆散射光与入射光之间的频率差V称为拉曼位移,拉曼位移与入射光频率无关,它只与散射分子本 身的结构有关。 ◆拉曼散射是由于分子极化率的改变而产生的。 ◆拉曼位移取决于分子振动能级的变化,不同化学键或基团有特征的分子振动,△E反映了指定能级 的变化,因此与之对应的拉曼位移也是特征的。这是拉曼光谱可以作为分子结构定性分析的依据
1. 拉曼光谱原理 ◆ 光是电磁辐射,其作用于物质,光子与物质分子发生碰撞时,产生散射光。 ◆ 当一束频率为V0的单色光照射到样品上后,分子可以使入射光发生散射。大部分光只是改变方向发 生散射,而光的频率仍与激发光的频率相同,弹性碰撞,这种散射称为瑞利散射。 ◆ 约占总散射光强度的 10-6~10-10的散射,不仅改变了光的传播方向,而且散射光的频率也改变了, 不同于激发光的频率,非弹性碰撞,称为拉曼散射。 ◆ 拉曼散射中频率减少的称为斯托克斯散射,频率增加的散射称为反斯托克斯散射,斯托克斯散射 通常要比反斯托克斯散射强得多,拉曼光谱仪通常测定的大多是斯托克斯散射,也统称为拉曼散 射。 ◆ 散射光与入射光之间的频率差V称为拉曼位移,拉曼位移与入射光频率无关,它只与散射分子本 身的结构有关。 ◆ 拉曼散射是由于分子极化率的改变而产生的。 ◆ 拉曼位移取决于分子振动能级的变化,不同化学键或基团有特征的分子振动,ΔE反映了指定能级 的变化,因此与之对应的拉曼位移也是特征的。这是拉曼光谱可以作为分子结构定性分析的依据