
第二部分:晶体的电子衍射
第二部分:晶体的电子衍射
衍射光路图如图所示。晶体的衍射方程为: 2dhk1sinθ=nX 或:2(dhk1/n)sin0=入 KJ2T样品 此式的意义是:dk1晶面的n级衍射可以看作是 反射球 dk1/n的1级衍射。注意到dk1的几何意义就容易 证明: dpkl/n=dnhnknl k/2π dphnkn称为衍射面,只有互质的(hkl)面才是 “真实的”的晶面。 于是,引入衍射面后衍射方程一统写成: ⊙ 2dpkisin 0=A 即把高级衍射也处理成布拉格反射,统用反射 球来描述。下面就电子衍射的特殊性作进一步 的处理。 R (1)波长短 衍射图记录面 电子波长入很小,因此0也很小,可以进行如 下近似: R=Ltan 0 ~Lsin 0
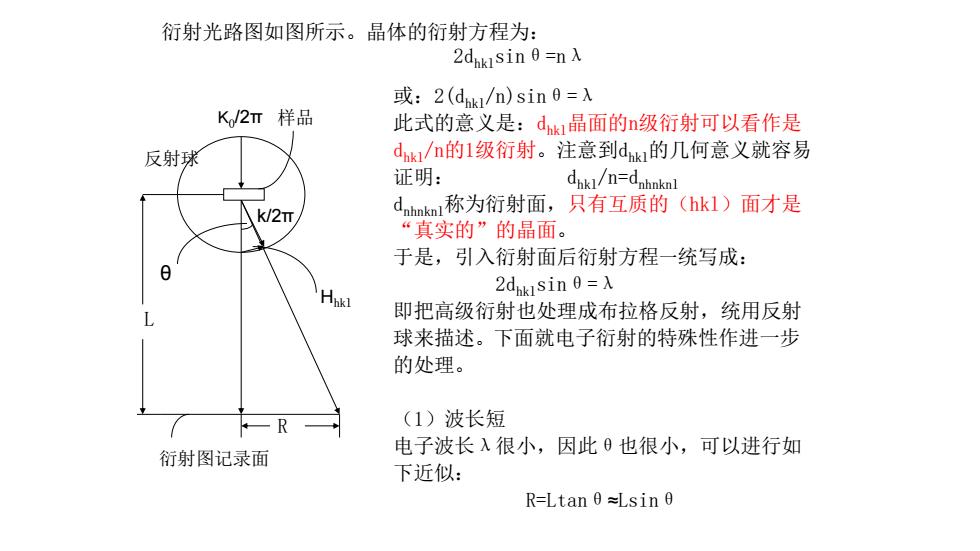
衍射光路图如图所示。晶体的衍射方程为: 2dhklsinθ=nλ θ Hhkl 反射球 K0 /2π k/2π L R 样品 或:2(dhkl/n)sinθ=λ 此式的意义是:dhkl晶面的n级衍射可以看作是 dhkl/n的1级衍射。注意到dhkl的几何意义就容易 证明: dhkl/n=dnhnknl dnhnknl称为衍射面,只有互质的(hkl)面才是 “真实的”的晶面。 于是,引入衍射面后衍射方程一统写成: 2dhklsinθ=λ 即把高级衍射也处理成布拉格反射,统用反射 球来描述。下面就电子衍射的特殊性作进一步 的处理。 (1)波长短 电子波长λ很小,因此θ也很小,可以进行如 下近似: R=Ltanθ≈Lsinθ 衍射图记录面

带入衍射方程得到: X=2dnkisine=2dpkiR/L 即: 2Rdnk=L A 这个结果给出了衍射点位置与晶面间距的关系,是重要的关系式。 称L入为电镜的相机常数。L称为相机长度,L=fMM。,o是电镜物镜焦距, M,M是中间镜与投影镜的放大率。通常使用200千伏的加速电压和80cm的 相机长度,此时的电镜相机常数是20.08mmA。 (2)强度大 电子束的强度很大使得衍射束依然很强,从而发生较强的多次衍射。常见 到的是二次衍射束,它是(hk1)面的衍射束恰好满足了(hkl)面的布拉 格条件时发生的再衍射(图略)。多次衍射的存在造成:①一些系统消光 的衍射点可能会出现。②衍射强度可能是多次衍射的叠加,这给衍射强度 的分析带来困难,使得解读单胞内部信息的工作困难重重
带入衍射方程得到: λ=2dhklsinθ=2dhklR/L 即: 2Rdhkl=Lλ 这个结果给出了衍射点位置与晶面间距的关系,是重要的关系式。 称Lλ为电镜的相机常数。L称为相机长度,L=f0MiMp ,f0是电镜物镜焦距, Mi,Mp是中间镜与投影镜的放大率。通常使用200千伏的加速电压和80cm的 相机长度,此时的电镜相机常数是20.08mmÅ。 (2)强度大 电子束的强度很大使得衍射束依然很强,从而发生较强的多次衍射。常见 到的是二次衍射束,它是(hkl)面的衍射束恰好满足了(h1k1l1)面的布拉 格条件时发生的再衍射(图略)。多次衍射的存在造成:①一些系统消光 的衍射点可能会出现。②衍射强度可能是多次衍射的叠加,这给衍射强度 的分析带来困难,使得解读单胞内部信息的工作困难重重

(3)样品薄 因为是记录透射信息,所以样品当然要薄到电子束能够穿透,在高分辨成像 情况下还要薄到能作相位体近似(最好到20-30m)。这样的薄样品有一个特 点:衍射点纵向展宽,用倒空间语言叙述就是倒易点拉长为倒易杆,如此我 们在记录零阶劳厄带衍射信息时会同时记录到高阶劳厄带的信息,这也给衍 射强度的分析造成了困难。 关于电子衍射图 记录到的是什么? a.纳米束电子衍射(NBD) b.汇聚束电子衍射(CBD) c.选区电子衍射(ED) 用平行光照明,在物镜的焦平面上插入圆孔光栏,得到的电子衍射称为选区 电子衍射(回光路图)。 优点:可选择特定的对象 夫琅和费衍射,傅立叶变换与倒易空间,记录面与倒易空间截面(图)
(3)样品薄 因为是记录透射信息,所以样品当然要薄到电子束能够穿透,在高分辨成像 情况下还要薄到能作相位体近似(最好到20-30nm)。这样的薄样品有一个特 点:衍射点纵向展宽,用倒空间语言叙述就是倒易点拉长为倒易杆,如此我 们在记录零阶劳厄带衍射信息时会同时记录到高阶劳厄带的信息,这也给衍 射强度的分析造成了困难。 关于电子衍射图 记录到的是什么? a.纳米束电子衍射(NBD) b.汇聚束电子衍射(CBD) c.选区电子衍射 (ED) 用平行光照明,在物镜的焦平面上插入圆孔光栏,得到的电子衍射称为选区 电子衍射(回光路图)。 优点:可选择特定的对象 夫琅和费衍射,傅立叶变换与倒易空间,记录面与倒易空间截面(图)

CBED是将具有足够大会聚角的电子束会 聚到试样上,将物镜后焦面上的透射斑 ☒ ✉ 点和衍射斑点扩展成一个个衍射盘。试 际分杂 后焦面 样的结构信息反映在圆盘中的各种衬度 常-直 花样上。 像平面 CBED的应用领域:晶体对称性(包括晶体 点群、空间群)、晶体点阵参数、薄晶片 厚度和晶体势函数、晶体和准晶体中位错 b矢量的测定,以及材料应变场研究
后焦面 像平面