第5章均匀平面波在无界空间中的传播(内容不用多修改了,不然格式会变化) 均匀平面波的概念 波阵面:空间相位相同的点构成的曲面,即等相位面 平面波:等相位面为无限大平面的电磁波 均匀平面波:等相位面上电场和磁场的方向、振幅都保持不变的平面波 均匀平面波是电磁波的一种理想情况,其分析方法简单,但又表征了电磁波的重要特性。 本章内容 5.1 理想介质中的均匀平面波 5.2 电磁波的极化 5.3 导电媒质中的均匀平面波 5.4 色散与群速 5.5均匀平面波在各向异性媒质中的传播 5.1理想介质中的均匀平面波 5.1.1 一维波动方程的均匀平面波解 5.1.2理想介质中均匀平面波的传播特点 5.1.3沿任意方向传播的均匀平面波 5.1,1一维波动方程的均匀平面波解 设在无限大的无源空间中,充满线性、各向同性的均匀理想介质。均匀平面波沿z轴传播, 则电场强度和磁场强度均不是x和y的函数,即 aE aE o,00-0→E=0,n=0 A-2 由于 6蓝装+-0→-0→6=0 月-设00-0>=n +2E.=0 同理 结论:均匀平面波的电场强度和磁场强度都垂直于波的传播方向一 横电磁波(TEM波) 设电场只有x分量,即 d'E,@+kE,(e)=0 E(e)=e,E,(e)→d正 其解为: E,(=)=Ae+e
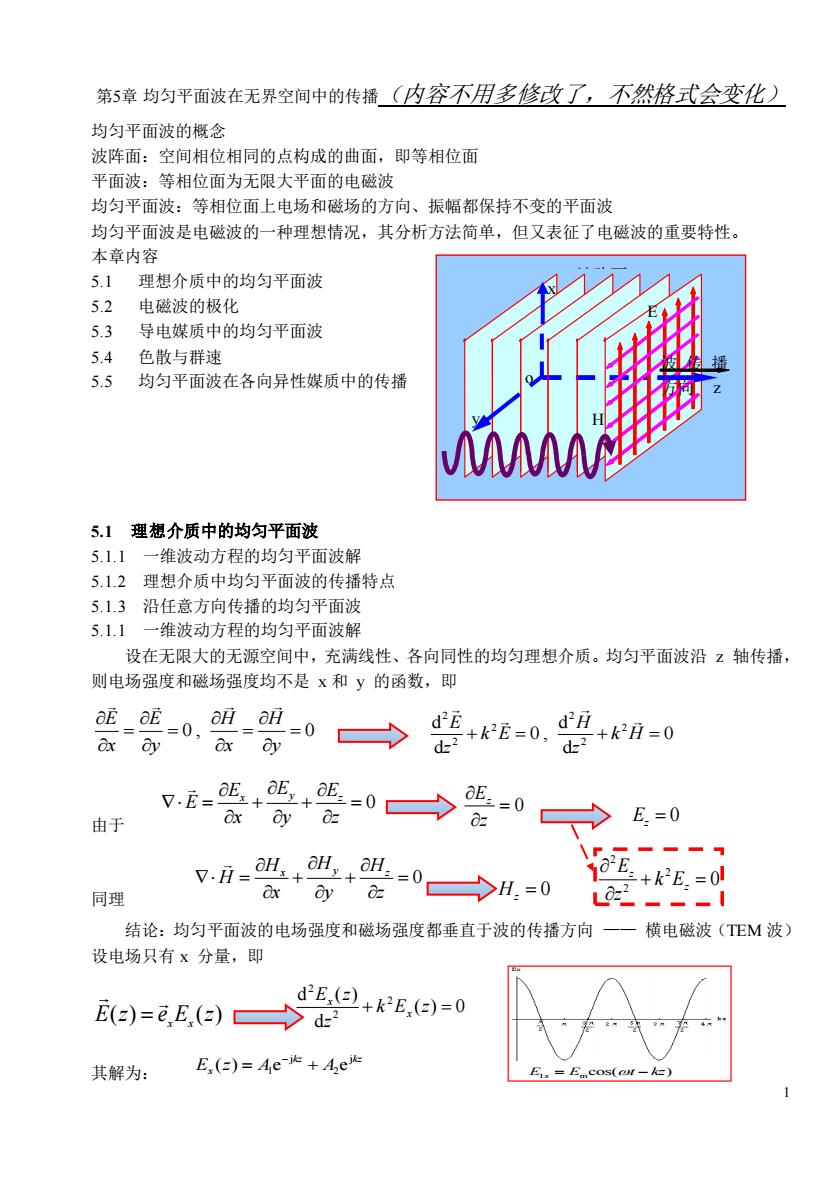
1 第5章 均匀平面波在无界空间中的传播(内容不用多修改了,不然格式会变化) 均匀平面波的概念 波阵面:空间相位相同的点构成的曲面,即等相位面 平面波:等相位面为无限大平面的电磁波 均匀平面波:等相位面上电场和磁场的方向、振幅都保持不变的平面波 均匀平面波是电磁波的一种理想情况,其分析方法简单,但又表征了电磁波的重要特性。 本章内容 5.1 理想介质中的均匀平面波 5.2 电磁波的极化 5.3 导电媒质中的均匀平面波 5.4 色散与群速 5.5 均匀平面波在各向异性媒质中的传播 5.1 理想介质中的均匀平面波 5.1.1 一维波动方程的均匀平面波解 5.1.2 理想介质中均匀平面波的传播特点 5.1.3 沿任意方向传播的均匀平面波 5.1.1 一维波动方程的均匀平面波解 设在无限大的无源空间中,充满线性、各向同性的均匀理想介质。均匀平面波沿 z 轴传播, 则电场强度和磁场强度均不是 x 和 y 的函数,即 0 , 0 E E H H x y x y = = = = 2 2 2 2 2 2 d d 0 , 0 d d E H k E k H z z + = + = 由于 0 x y z E E E E x y z = + + = 0 E z z = 0 E z = 同理 0 x y z H H H H x y z = + + = 0 H z = 2 2 2 0 z z E k E z + = 结论:均匀平面波的电场强度和磁场强度都垂直于波的传播方向 —— 横电磁波(TEM 波) 设电场只有 x 分量,即 E(z) e E (z) x x = ( ) 0 d d ( ) 2 2 2 + k E z = z E z x x k = 其解为: j j 1 2 ( ) e e kz kz E z A A x − = + E H z 波传播 方向 波阵面 x y o 的波形 1 mcos( ) E E t kz x = −
解的物理意义 第一项 E(=)=Aeik=Eeleik E(=,t)=Re[Eeiue ieic ]Em cos(ot-k+) 可见,4e表示沿±:方向传播的波。 第二项 E.e)=4c=Ecc←、 E(,1)=Re[Emeieei ]=Em cos(+) 沿一z方向传播 相伴的磁场 由7×E=-j@H,可得 磁场与电场相互 垂直,且同相位 e.xE ou dz E) 其中 称为媒质的本征阻拉。在真空中 凸=120x=3779 n=- 同理,对于 E2=eE,=e heik 结论:在理想介质中,均匀平面波的电场强度与磁场强度相互垂直,且同相位 5.1.2理想介质中均匀平面波的传播特点 1.均匀平面波的传播参数 (1)角频率、频率和周期 角频率。:表示单位时间内的相位变化,单位为rad/s 周期T:时间相位变化2π的时间间隔,即 OT-2 ( 频率f: (2)波长和相位常数 波长入:空间相位差为2丌的两个波阵面的间距,即 E(0.1)=Ecosor
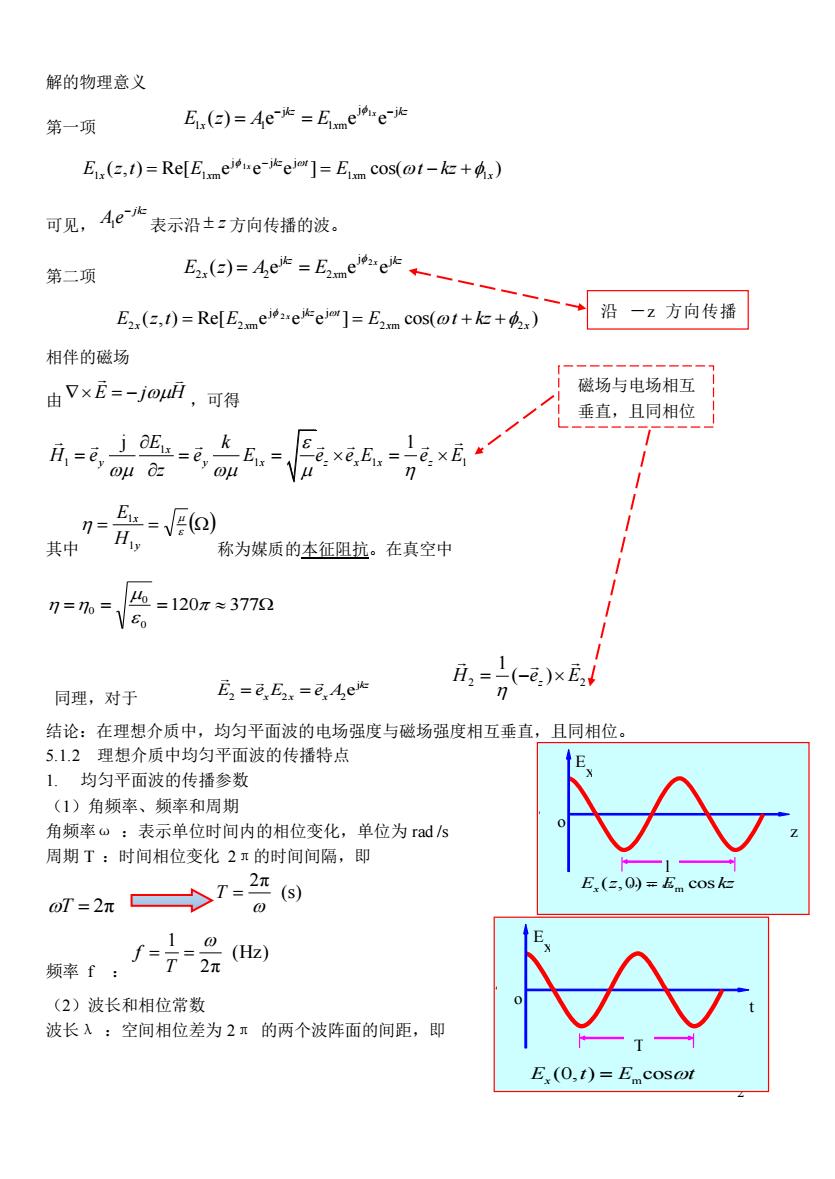
2 解的物理意义 第一项 1 j j j 1 1 1 m ( ) e e e kz kz x E z A E x x − − = = 1 j j j 1 1 m 1 m 1 ( , ) Re[ e e e ] cos( ) x kz t E z t E E t kz x x x x − = = − + 可见, jkz Ae − 1 表示沿 z 方向传播的波。 第二项 2 j j j 2 2 2 m ( ) e e e kz kz x E z A E x x = = 2 j j j 2 2 m 2 m 2 ( , ) Re[ e e e ] cos( ) x kz t E z t E E t kz x x x x = = + + 相伴的磁场 由 E j H = − ,可得 1 1 1 1 1 j 1 x y y x z x x z E k H e e E e e E e E z = = = = 其中 = = () y x H E 1 1 称为媒质的本征阻抗。在真空中 = = =120 377 0 0 0 同理,对于 j 2 2 2e kz E e E e A = = x x x 2 2 ( ) 1 H ez E = − 结论:在理想介质中,均匀平面波的电场强度与磁场强度相互垂直,且同相位。 5.1.2 理想介质中均匀平面波的传播特点 1. 均匀平面波的传播参数 (1)角频率、频率和周期 角频率ω :表示单位时间内的相位变化,单位为 rad /s 周期 T :时间相位变化 2π的时间间隔,即 T = 2π 2π T (s) = 频率 f : 1 (Hz) 2π f T = = (2)波长和相位常数 波长λ :空间相位差为 2π 的两个波阵面的间距,即 沿 -z 方向传播 的波 磁场与电场相互 垂直,且同相位 t T o x E E t E t x (0, ) cos = m o x E l z E z E kz x ( ,0) cos 的曲线 = m

a:a女-祭-应m 1 相位常数k:表示波传播单位距离的相位变化 k=2(adm) k的大小等于空间相位2π内所包含的波长数目,因此也称为波数 (3)相速(波速) 相速:电磁波的等相位面在空间中的移动速度 由o-k=C>o-k他=0 故得到均匀平面波的相速为 1m/9)←- 相速只与媒质参数有关,而 与电磁波的频率无关 1 1 v=C=- =3×103(m/s) 480 真空中: x10×3610 2、能量密度与能流密度 由于 =×E 电场能量与磁场能量相同 ,于是有 "=5s=3川=w一 故 p=w。+wn=e武=l 理想介质中均有 5=xie0=ecasio-k+A) 面波的和 wRe()x -总8 ="-→ 能量的传输速度等于相速 3、理想介质中的均匀平面波的传播特点(P196页) 根据前面的分析,可总结出理想介质中的均匀平面波的传播特点为: (1)电场、磁场与传播方向之间相互垂直,是横电磁波(TEM波)。 (2)无衰减,电场与磁场的振幅不变。 (3)波阻抗为实数,电场与磁场同相位。 (4)电磁波的相速与频率无关,无色散。 (⑤)电场能量密度等于磁场能量密度,能量的传输速度等于相速
3 k = 2π 2π 1 (m) k f = = 相位常数 k :表示波传播单位距离的相位变化 2π k (rad/m) = k 的大小等于空间相位 2π内所包含的波长数目,因此也称为波数。 (3)相速(波速) 相速 v:电磁波的等相位面在空间中的移动速度 由 t −kz =C d d 0 t k z − = 故得到均匀平面波的相速为 (m s) 1 d d = = = = t k z v 真空中: 8 0 0 7 9 1 1 3 10 (m/s) 1 4π 10 10 36π v c − − = = = = 2、能量密度与能流密度 由于 H ez E = 1 ,于是有 2 2 e m 1 1 2 2 w E H w = = = 故 2 2 w w w E H e m = + = = 2 2 m 1 ( , ) ( , ) cos ( ) 2 S E z t H z t e E t kz z x = = − + 2 2 av m m 1 1 2 2 w E H = = * 2 av m 1 1 Re[ ( ) ( )] 2 2 S E z H z e E z = = 2 m av 1 1 2 z e E w v = = 3、理想介质中的均匀平面波的传播特点(P196 页) 根据前面的分析,可总结出理想介质中的均匀平面波的传播特点为: (1)电场、磁场与传播方向之间相互垂直,是横电磁波(TEM 波)。 (2)无衰减,电场与磁场的振幅不变。 (3)波阻抗为实数,电场与磁场同相位。 (4)电磁波的相速与频率无关,无色散。 (5)电场能量密度等于磁场能量密度,能量的传输速度等于相速。 相速只与媒质参数有关,而 与电磁波的频率无关 电场能量与磁场能量相同 能量的传输速度等于相速 x y z E H O 理想介质中均匀平 面波的 和 E H

例5.1.1频率为9.4GH的均匀平面波在聚乙烯中传播,设其为无耗材料,相对介电常数为 £,=226。若磁场的振幅为7mm,求相速、波长、波阻抗和电场强度的幅值。 解:由题意 6,=2.26,f=9.4×10°Hz 因此 _1.996×10 =710 =2.12m 、377 n后左26210 Em=Hn=7×103×251=1.757V/m 例5.1.2 均匀平面波的感场强度的振相为行4 ,以相位常数为30radm在空气中沿一e方 向传插。当1=0和:=0时,若户取向为一已,试写出E和户的表示式,并求出频率和波长。 解:以余弦为基准,直接写出 i(e,0=-6,3元oso+B阳)ANm E(=,1)=nH(=,t)x(-e.)=e40cos(ot+Bz)V/m 因B=30rad/m,故 =音-新=021m,-号g-兰0=1450业 B30 则 月e,0=-6元co90x101+30a)Wm E(,=e,40cos(90×101+30z)Vm 例5.1.3频率为100Mz的均匀电磁波,在一无耗媒质中沿+: 该媒质的相对介电常数8,=4、相对磁导率4,=1,且当t一
4 例 5.1.1 频率为 9.4GHz 的均匀平面波在聚乙烯中传播,设其为无耗材料,相对介电常数为 r = 2.26 。若磁场的振幅为 7mA/m,求相速、波长、波阻抗和电场强度的幅值。 解:由题意 9 r = = 2.26 , 9.4 10 Hz f 因此 0 0 8 r 1.996 10 m/s 2.26 v v v = = = 8 9 1.996 10 2.12 m 9.4 10 v f = = = 0 r 377 251 2.26 = = = = 3 m m E H 7 10 251 1.757 V/m − = = = 例 5.1.2 均匀平面波的磁场强度的振幅为 A m 3 1 ,以相位常数为 30 rad/m 在空气中沿 z e − 方 向传播。当 t = 0 和 z = 0 时 ,若 H 取向为 y e − ,试写出 E 和 H 的表示式,并求出频率和波长。 解:以余弦为基准,直接写出 1 ( , ) cos( ) A/m 3π H z t e t z = − + y E(z,t) =0H(z,t)(−e z ) = e x 40cos(t + z) V/m 因 = 30rad m ,故 2π 2π 0.21 m , 30 === 8 3 10 45 8 9 10 1.43 10 Hz π /15 π c f = = = = 则 1 8 ( , ) cos(90 10 30 ) A/m 3π H z t e t z = − + y ( , ) 40cos(90 10 30 ) V/m 8 E z t e t z = x + 例 5.1.3 频率为 100Mz 的均匀电磁波,在一无耗媒质中沿 + z 方向传播,其电场 xEx E e = 。已知 该媒质的相对介电常数 r = 4 、相对磁导率 r =1 ,且当 t = 0 t = 0、z =1 8m 时,电场幅值为

10V/m。试求电场强度和磁场强度的瞬时表示式。 解:设电场强度的瞬时表示式为 E(=,1)=eE,=e,10cos(@t-k+) 式中0=2对=2πx103rads =am-吕-adn 对于余弦函数,当相角为零时达振幅值。考虑条件t=0、z=1/8m时,电场达到幅值,得 =北=经君 所以 c0-=10广co2a×101-经:+2 -a10cs2rx101-经e-g》Vm 月=×E=, 磁场强度的瞬时表示式为 =60m0 式中 e,0=g,0os2mx101-音e-g】n 104 因此 例5.1.4自由空间中平面波的电场强度 E=e.50cos(ot-k)V/m 求在=0处垂直穿过半径R=2.5m的圆平面的平均功率。 解:电场强度的复数表示式为E=E,50e大 自由空间的本征阻抗为 %=120π2 故得到该平面波的磁场强度 7
5 V m -4 10 。 试求电场强度和磁场强度的瞬时表示式。 解:设电场强度的瞬时表示式为 4 ( , ) 10 cos( ) x x x z t E t kz − E e e = = − + 式中 8 = = 2π 2π 10 rad/s f 8 r r 8 2π 10 4 4 π rad/m 3 10 3 k c = = = = 对于余弦函数,当相角为零时达振幅值。考虑条件 t = 0、z =1/8 m 时,电场达到幅值,得 4π 1 π 3 8 6 = = = kz 所以 4 8 4π π ( , ) 10 cos(2π 10 ) 3 6 E z t e t z x − = − + 4 8 4π 1 10 cos[2π 10 ( )] V/m 3 8 x e t z − = − − 磁场强度的瞬时表示式为 1 1 H e E e E z y x = = 式中 0 r 60π = = = 因此 4 10 4 1 8 ( , ) cos[2π 10 π( )] A/m 60π 3 8 H z t e t z y − = − − 例 5.1.4 自由空间中平面波的电场强度 E e t kz = − x 50cos( ) V/m 求在 0 z = z 处垂直穿过半径 R = 2.5m 的圆平面的平均功率。 解:电场强度的复数表示式为 j 50e kz E ex − = 自由空间的本征阻抗为 0 = 120π 故得到该平面波的磁场强度 j 0 5 e A/m 12π kz y y E H e e − = =