
第3章静态电磁场及其边值问题的解 第4章0 静态电磁场:场量不随时间变化,包括:静电场、恒定电场和恒定磁场 时变情况下,电场和磁场相互关联,构成统一的电磁场 静态情况下,电场和磁场由各自的源激发,且相互独立 本章内容 3.1静电场分析 3.2导电媒质中的恒定电场分析 3.3恒定磁场分析 3.4静态场的边值问题及解的惟一性定理 3.5镜像法 36分离变量 3.1静电场分析 静电场的应用: 静电放电:高电压测量测量中用到的球隙 静电感应:传感器,电容式物位计。 静电屏蔽:高电压实验室,微波暗室,通信电缆等 电场力的应用:电子管,晶体管,阴极射线管,显像管,静电发电机,静电电动机,回旋加速器。 工业:静电除尘,静电分离,静电喷漆,静电复印机。 静电场的危害:静电感应引起高压电线对周围的影响。静电引发火灾,静电防护。 3.1静电场分析 本节内容 311 静电场的基本方程和边界条件 3.1.2 电位函数 313 导体系统的电容与部分电容 3.1.4 静电场的能量 3.1.5静电力 3.1.1静电场的基本方程和边界条件 1.基本方程 (V.D=p f.D.ds=g 微分形式 fE-di=0 积分形式 7×E=0 D=E本构关系 2.边界条件
1 第3章 静态电磁场及其边值问题的解 第4章 () 静态电磁场:场量不随时间变化,包括:静电场、恒定电场和恒定磁场 时变情况下,电场和磁场相互关联,构成统一的电磁场 静态情况下,电场和磁场由各自的源激发,且相互独立 本章内容 3.1 静电场分析 3.2 导电媒质中的恒定电场分析 3.3 恒定磁场分析 3.4 静态场的边值问题及解的惟一性定理 3.5 镜像法 3.6 分离变量法 3.1 静电场分析 静电场的应用: 静电放电:高电压测量测量中用到的球隙 静电感应:传感器,电容式物位计。 静电屏蔽:高电压实验室,微波暗室,通信电缆等 电场力的应用:电子管,晶体管,阴极射线管,显像管,静电发电机,静电电动机,回旋加速器。 工业:静电除尘,静电分离,静电喷漆,静电复印机。 静电场的危害:静电感应引起高压电线对周围的影响。静电引发火灾,-静电防护。 3.1 静电场分析 本节内容 3.1.1 静电场的基本方程和边界条件 3.1.2 电位函数 3.1.3 导体系统的电容与部分电容 3.1.4 静电场的能量 3.1.5 静电力 3.1.1 静电场的基本方程和边界条件 1. 基本方程 微分形式 = = E 0 D 积分形式 = = d 0 d E l D S C S q D E 本构关系 = 2. 边界条件

e。D,-D)=ps D。-D2n=Ps e×(E,-E2)=0 E:-E21=0 若分界面上不存在面电荷,即P=0,则 介质1 个质2 e.(D,-D2)=0 ex(E,-E)=0 或 场矢量的折射关系 an8-E,/E2=/D。=5 tan 0,Ex/E2n 621D2m62 导体表面的边界条件 在静电平衡的情况下,导体内部的电场为0,则导体表面的边界条件为 [D=Ps (D=Ps En×E=0 或 E,=0 3.1.2电位函数 1.电位函数的定义 的 V×E=0>E=-V0 即静电场可以用一个标量函数的梯度来表示,标量函数称为静电场的标量电位或简称电位。 2.电位的表达式 对于连续的体分布电荷,由 R=F-T E(F)= 4πJh dV'= 4Ep(H =-X克叮 R 故得 )avc 1 同理得,面电荷的电位: 1exar+c 线电荷的电位: o)=4元cR
2 − = − = ( ) 0 ( ) n 1 2 n 1 2 E E D D e e S 或 − = − = 1t 2t 0 1n 2n E E D D S 若分界面上不存在面电荷,即 S = 0 ,则 − = − = ( ) 0 ( ) 0 n 1 2 n 1 2 E E D D e e 或 = = 1t 2t 1n 2n E E D D 场矢量的折射关系 2 1 2 2n 1 1n 2t 2n 1t 1n 2 1 / / / / tan tan = = = D D E E E E 导体表面的边界条件 在静电平衡的情况下,导体内部的电场为 0,则导体表面的边界条件为 = = n 0 n E D e e S 或 = = t 0 n E D S 3.1.2 电位函数 1. 电位函数的定义 由 E = 0 E = − 即静电场可以用一个标量函数的梯度来表示,标量函数 称为静电场的标量电位或简称电位。 2. 电位的表达式 对于连续的体分布电荷,由 )d ] 1 ( )( 4π 1 [ )d 1 ( ) ( 4π 1 d ( ) 4π 1 ( ) 3 V R r V R V r R r R E r V V V = − = − = 故得 ( ) V C R r r V + = d ( ) 4π 1 同理得,面电荷的电位: S C R r r S S + = d ( ) 4π 1 ( ) 3 线电荷的电位: ( ) l C R r r C l + = d ( ) 4π 1 介质 2 介质 1 2 1 2 1 E2 E1 en R = r − r 3 1 R R R = −

点电荷的电位: of)-+c 3.电位差 将E=-Vp两端点乘dl,则有 E-dJ-Vo-dj-(ddd)-dp dy av 上式两边从点P到点Q沿任意路径进行积分,得 Eidi=-do-P)-) 电场力做的功 P、Q两点间的电位差 关于电位差的说明 P、Q两点间的电位差等于电场力将单位正电荷从P点移至Q点所做的功,电场力使单位正电荷 由高电位处移到低电位处。 申位差也称为申压,可用U表示。 电位差有确定值,只与首尾两点位置有关,与积分路径无关。 4由位参考点 静电位不惟一,可以相差一个常数,即 0-p+C→Vp-(0+C)=7p 为使空间各点电位具有确定值,可以选定空间某一点作为参考点,且令参考点的电位为零,由 于空间各点与参考点的电位差为确定值,所以该点的电位也就具有确定值,即 选参考点 令参考点电位为零 电位确定值(电位差) 两点间电位差有定值 选择电位参考点的原则 ()应使电位表达式有意义。(3)同一个问题只能有一个参考点。 (2)应使电位表达式最简单。若电荷分布在有限区域,通常取无限远作电位参考点。 例3.1.1求电偶极子的电位
3 点电荷的电位: ( ) C R q r = + 4π 3. 电位差 将 E = − 两端点乘 l d ,则有 d d ( d d d ) = −d + + = − = − y y y y x x E l l 上式两边从点 P 到点 Q 沿任意路径进行积分,得 E dl d (P) (Q) Q P Q P = − = − 关于电位差的说明 P、Q 两点间的电位差等于电场力将单位正电荷从 P 点移至 Q 点所做的功,电场力使单位正电荷 由高电位处移到低电位处。 电位差也称为电压,可用 U 表示。 电位差有确定值,只与首尾两点位置有关,与积分路径无关。 4. 电位参考点 静电位不惟一,可以相差一个常数,即 = +C = ( +C) = 为使空间各点电位具有确定值,可以选定空间某一点作为参考点,且令参考点的电位为零,由 于空间各点与参考点的电位差为确定值,所以该点的电位也就具有确定值,即 选择电位参考点的原则 (1)应使电位表达式有意义。(3)同一个问题只能有一个参考点。 (2)应使电位表达式最简单。若电荷分布在有限区域,通常取无限远作电位参考点。 例 3.1.1 求电偶极子的电位. 1 2 2 1 0 1 2 4π 0 ) 1 1 ( 4π ( ) rr q r r r r q r − = − = 电场力做的功 P、Q 两点间的电位差 选参考点 令参考点电位为零 电位确定值(电位差) 两点间电位差有定值
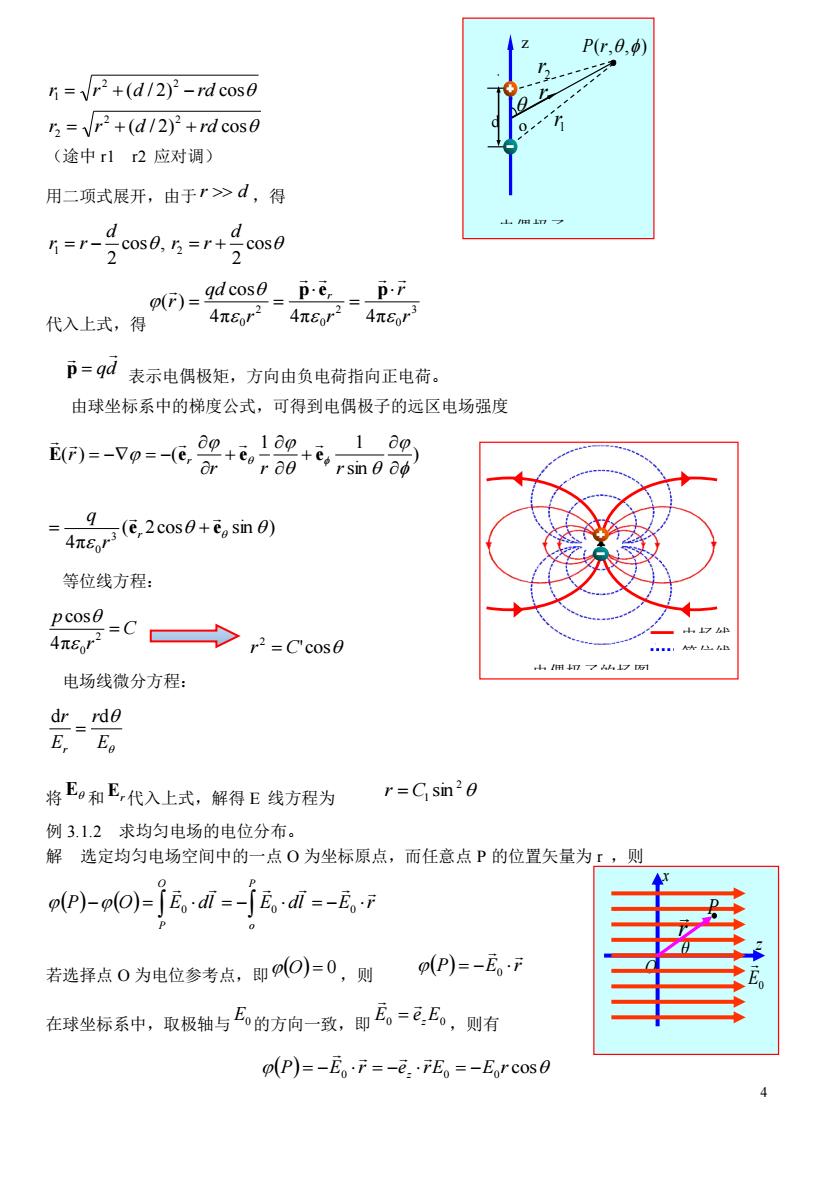
P(r.0.0 片=Vr2+(d/2)2-rd cos8 +(d/2)+rdcos0 (途中r12应对调) 用二项式展开,由于r>d,得 d 山mn一 =r-号m85=r+号ow0 代入上式,得 n恶 D=9d表示电偶极矩,方向由负电荷指向正电荷: 由球坐标系中的梯度公式,可得到电偶极子的远区电场强度 1a0 -4ze2os0+8,sm0) 等位线方程: pcos0 4C→,=Cs0 电场线微分方程: d业_d0 E Eo 将E0和E,代入上式,解得E线方程为 r=C sin20 例3.12求均匀电场的电位分布。 解选定均匀电场空间中的一点0为坐标原点,而任意点P的位置矢量为r,则 pp)-po)=fE,di=-a。d=-E元 若选择点0为电位参考点,即O)=0,则 (P=-E·F 在球坐标系中,取极轴与瓦的方向一致,即瓦。=.E。,则有 p(P)=-E。·F=-e.·E。=-Ercos0
4 ( / 2) cos ( / 2) cos 2 2 2 2 2 1 r r d rd r r d rd = + + = + − (途中 r1 r2 应对调) 用二项式展开,由于 r d ,得 cos , 2 1 d r = r − cos 2 2 d r = r + 代入上式,得 3 0 2 0 2 4π 0 4π 4π cos ( ) r r r r qd r r = = = p e p qd p = 表示电偶极矩,方向由负电荷指向正电荷。 由球坐标系中的梯度公式,可得到电偶极子的远区电场强度 ) sin 1 1 ( ) ( + + = − = − r r r r r E e e e ( 2cos sin ) 4π 3 0 e e = r + r q 等位线方程: C r p = 2 4π 0 cos 'cos 2 r = C 电场线微分方程: E r E r r d d = 将 E 和 Er 代入上式,解得 E 线方程为 2 1 r = C sin 例 3.1.2 求均匀电场的电位分布。 解 选定均匀电场空间中的一点 O 为坐标原点,而任意点 P 的位置矢量为 r ,则 (P) (O) E dl E dl E r P o O P − = = − = − 0 0 0 若选择点 O 为电位参考点,即 (O) = 0 ,则 (P) E r = − 0 在球坐标系中,取极轴与 E0 的方向一致,即 0 E0 E ez = ,则有 (P) = −E0 r = −ez rE0 = −E0 r cos + q 电偶极子 z d o - q 1 r 2 r r P(r,,) 等位线 电场线 电偶极子的场图 E0 x z O P r

在圆柱坐标系中,取瓦与x轴方向一致,即E,=,而=,P+区:,故 p(P)=-E。·F=-e·Eenp+e.)=-Eopcos 例3.1.3求长度为2L、电荷线密度为P0的均匀带电线的电位。 解采用圆柱坐标系,令线电荷与z轴相重合,中点位于坐标原点。由于轴对称性,电位与无 关,在带电线上位于:处的线元d=正,它到点P0、女、)的距离R=D+(-),则 F)=P。r」 1 p+-出 -++-] d/'=d=' =mhp+-F-) 46p2+6+L-(+) 在上式中若令L→0,则可得到无限长直线电荷的电位。当L>R时,上武可写为 s会hD+正+'=ahD+E+L.h2马 4π6 P+-L 46 p 2π6p 当L→∞时,上式变为无穷大,这是因为电荷不是分布在有限区域内,而将电位参考点选在无穷 远点之故。这时可在上式中加上一个任意常数,则有 会兴c 并选择有限远处为电位参考点。例如,选择p=a的点为电位参考点,则有 C=2L 26atf)=,h4 2π6p 5.电位的微分方程 在均匀介质中,有 ,1标量泊松方程 V.D=p-V.E=p/s E=-V0 V'o=-pls 在无源区城,p=0→☑0=0.拉普拉斯方程
5 在圆柱坐标系中,取 E0 与 x 轴方向一致,即 0 E0 E ex = ,而 r e e zz = + ,故 (P) = −E0 r = −ex E0 (e + ez z) = −E0 cos 例 3.1.3 求长度为 2L、电荷线密度为 l0 的均匀带电线的电位。 解 采用圆柱坐标系,令线电荷与 z 轴相重合,中点位于坐标原点。由于轴对称性,电位与 无 关。在带电线上位于 z 处的线元 dl = dz ,它到点 p(、、z) 的距离 ( ) 2 2 R = + z − z ,则 ( ) ( ) ( ) ( ) ( ) (z L) (z L) z L z L z z z z dz z z r l L L l L L l + + − + + − − − = = − + + − + − = − − 2 2 2 2 0 0 2 2 0 0 2 2 0 0 ln 4 ln | 4 1 4 在上式中若令 L → ,则可得到无限长直线电荷的电位。当 L R 时,上式可写为 ( ) L L L L L L L r l l l 2 ln 2 ln 4 ln 4 0 0 2 2 0 0 2 2 2 2 0 0 + + = + − + + 当 L → 时,上式变为无穷大,这是因为电荷不是分布在有限区域内,而将电位参考点选在无穷 远点之故。这时可在上式中加上一个任意常数,则有 ( ) C L r l = + 2 ln 2 0 0 并选择有限远处为电位参考点。例如,选择ρ= a 的点为电位参考点,则有 a L C l 2 ln 2 0 0 = ( ) a r l ln 2 0 0 = 5. 电位的微分方程 在均匀介质中,有 = − = = E D E = − 2 在无源区域, = 0 0 2 = x y z L - L ( , , ) z z' d d l z = R 标量泊松方程 拉普拉斯方程