《电磁场理论》课程电子教案（讲义）第四章 时变电磁场

第四章时变电磁场 本章内容 41 波动方程 42 电磁场的位函数 4.3 电磁能量守恒定律 44 惟一性定理 4.5 时谐电磁场 1波动方程 1.问题的提出： 麦克斯韦方程 ,一阶矢量微分方程组，描述电场与磁场间的相互作用关系。 波动方程 ,二阶矢量微分方程，揭示电磁场的波动性 麦克斯韦方程组 波动方程。 2.无源区的波动方程 在无源空间中，设媒质是线性、各向同性且无损耗的均匀媒质，则有电磁波动方程： V2E-4 8E =0 n=0 -ar 推证 Vxh=6OE aH v.月=0 V.E=0 vxvx月=Vx(eE) 所-n=-4e0a 同理可得 v-m50 3问题： 若为有源空间，结果如何？若为导电媒质，结果如何 4.2 电磁场的位函数

1 2 2 ( ) t H H H     − = −     2 0 2 2 2 =    − t H H    第四章 时变电磁场 本章内容 4.1 波动方程 4.2 电磁场的位函数 4.3 电磁能量守恒定律 4.4 惟一性定理 4.5 时谐电磁场 .1 波动方程 1.问题的提出： 麦克斯韦方程 —— 一阶矢量微分方程组，描述电场与磁场间的相互作用关系。 波动方程 —— 二阶矢量微分方程，揭示电磁场的波动性。 麦克斯韦方程组 波动方程。 2.无源区的波动方程 在无源空间中，设媒质是线性、各向同性且无损耗的均匀媒质，则有电磁波动方程： 0 2 2 2 =    − t E E    0 2 2 2 =    − t H H    推证      =  =    = −    = 0 0 Ε H t H Ε t Ε H         同理可得 0 2 2 2 =    − t E E    3.问题： 若为有源空间，结果如何？若为导电媒质，结果如何？ 4.2 电磁场的位函数 ( ) t E H    =    

讨论内容：位函数的定义位函数的性质位函数的规范条件位函数的微分方程 1.引入位函数的意义 引入位函数来描述时变电磁场，使一些问题的分析得到简化。 2.位函数的定义 V.D=p V.B=0→B=V×A a D=sE、E= VxE=. aB -Vo)=P A at→ V×(E+sw.(-a1 -Vo 3.位函数的不确定性 -v.A+4s2=0 满足下列变换关系的两组位函数和中能描述同一个电憾场慰。刀任意可微函数 [=A+Vw p-ug=-2 aw 0=p-a V×A=V×(A+Vw)=V×A -vo:-04-v(9-ov)-3(A+9w)- aA 也就是说，对一给定的电磁场可用不同的位函数来描述。 不同位函数之间的上述变换称为规范变换。 原因：未规定A的散度。 4.位函数的规范条件 造成位函数的不确定性的原因就是没有规定A的散度。利用位函数的不确定性，可通过规定A的 散度使位函数满足的方程得以简化 在电磁理论中，通常采用洛仑兹条件，即 .+-0 除了利用洛仑兹条件外，另一种常用的是库仑条件，即 7.A=0 5.位函数的微分方程 同样 2a-9m0 =- at

2 讨论内容：位函数的定义 位函数的性质 位函数的规范条件 位函数的微分方程 1.引入位函数的意义 引入位函数来描述时变电磁场，使一些问题的分析得到简化。 2.位函数的定义  B = 0  B A   =  t B Ε    = −   ( ) = 0    + t A Ε   −   = − t A E   3.位函数的不确定性 满足下列变换关系的两组位函数 A 和Φ 能描述同一个电磁场问题。Φ为任意可微函数 A A t       = +       = −   即： ( ) ( ) ( ) A A A A A A t t t t         =   +  =           − − = − − − +  = − −       也就是说，对一给定的电磁场可用不同的位函数来描述。 不同位函数之间的上述变换称为规范变换。 原因：未规定 → A 的散度。 4.位函数的规范条件 造成位函数的不确定性的原因就是没有规定 → A 的散度。利用位函数的不确定性，可通过规定 → A 的 散度使位函数满足的方程得以简化。 在电磁理论中，通常采用洛仑兹条件，即 = 0    + t A    除了利用洛仑兹条件外，另一种常用的是库仑条件，即  A = 0  5. 位函数的微分方程 同样      = −    − 2 2 2 t J t A A     = −    − 2 2 2  D =    −   = = − t A D E E     、  − =    (− ) t A  = 0    + t A         = −    − 2 2 2 t

6.说明 a应用洛仑兹条件的特点：①位函数满足的方程在形式上是对称的，且比较简单，易求解： ②解的物理意义非常清楚，明确地反映出电磁场具有有限的传递速度：③矢量位只决定于 J,标量位只决定于P,这对求解方程特别有利。只需解出A,无需解出P就可得到待求的 电场和磁场。 b.电磁位函数只是简化时变电磁场分析求解的一种辅助函数，应用不同的规范条件，矢量位A 和标量位P的解也不相同，但最终得到的电磁场矢量是相同的。 7.问题 若应用库仑条件，位函数满足什么样的方程？具有什么特点？ 4.3电磁能量守恒定律 讨论内容：电磁能量及守恒关系；坡印廷定理；坡印廷矢量 1.电磁能量及守恒关系 电场能量密度，收-万 磁场能量密度： ”-B 电疆能量密度，=+=E.+H,B 空间区域V中的电磁能量 =可nmr=j,ED+HaW 特点：当场随时间变化时，空间各点的电磁场能量密度也要随 时间改变，从而引起电磁能量流动。 电磁能量守恒关系： 进入体积V的能量=体积V内增加的能量+体积V内损耗的能量 2.坡印廷定理 表征电磁能量守恒关系的定理 0(E.D+B+E-J 微分形式： -v.(E×m=a5 积分形式： -医xma5-.0+n-a+Eja 2

3 6.说明 a. 应用洛仑兹条件的特点：① 位函数满足的方程在形式上是对称的，且比较简单，易求解； ② 解的物理意义非常清楚，明确地反映出电磁场具有有限的传递速度；③ 矢量位只决定于 J，标量位只决定于ρ，这对求解方程特别有利。只需解出 A，无需解出  就可得到待求的 电场和磁场。 b. 电磁位函数只是简化时变电磁场分析求解的一种辅助函数，应用不同的规范条件，矢量位 A 和标量位  的解也不相同，但最终得到的电磁场矢量是相同的。 7.问题 若应用库仑条件，位函数满足什么样的方程? 具有什么特点? 4.3 电磁能量守恒定律 讨论内容:电磁能量及守恒关系; 坡印廷定理; 坡印廷矢量 1. 电磁能量及守恒关系 电场能量密度： e 1 2 w =  E D 磁场能量密度： m 1 2 w =  H B 电磁能量密度： e m 1 1 2 2 w w w E D = + =  +  H B 空间区域 V 中的电磁能量: 1 1 d ( )d V V 2 2 W w V E D H B V = =  +    特点：当场随时间变化时，空间各点的电磁场能量密度也要随 时间改变，从而引起电磁能量流动。 电磁能量守恒关系： 进入体积 V 的能量＝体积 V 内增加的能量＋体积 V 内损耗的能量 2. 坡印廷定理 表征电磁能量守恒关系的定理 微分形式： E D H B E J t E H          +  +    −  = ) 2 1 2 1 ( ) ( 积分形式：    −   =  +  +  S V V E D H B V E J V t E H S )d d 2 1 2 1 ( d d ( ) d         

.写e0raar SE.Jav -f.(E×H)d 通过曲面S进入体积V的电磁功率。 推证 P×A=了+0 E.v×月=Ej+E.0 由 at x0 月.vxE=-月.明 将以上两式相减，得到 E.vx月-月vxE=E.j+E.D+月.通 在线性和各向同性的媒质中，当参数都不随时间变化时，则有 E.V×H-H.7×E=-7.(E×而 E.OD-E.OE1(E.E)(E.D) 月. -明.0=uA面-0A =24 8t2 再利用矢量恒等式： 即可得到坡印廷定理的微分形式： -V(E×H)= -8ErnE 在任意闭曲面S所包围的体积V上，对上式两瑞积分，并应用散度定理，即可得到坡印廷定理

4 其中：   +  V E D H B V t )d 2 1 2 1 ( d d       V E J dV    −   S E H S    ( ) d 通过曲面 S 进入体积 V 的电磁功率。 推证        = −    = + t B Ε t D H J      将以上两式相减，得到 t B H t D Ε H H Ε Ε J Ε   +     −  =  +            在线性和各向同性的媒质中，当参数都不随时间变化时，则有 ) 2 1 ( ( ) 2 1 Ε D t t Ε Ε t Ε Ε t D Ε            =    =   =       ) 2 1 ( ( ) 2 1 H B t t H H t H H t B H            =    =   =       再利用矢量恒等式： 即可得到坡印廷定理的微分形式: Ε D H B Ε J t Ε H          +  +    −  = ) 2 1 2 1 ( ) ( 在任意闭曲面 S 所包围的体积 V 上，对上式两端积分，并应用散度定理，即可得到坡印廷定理 由        = −     =  +  t B H Ε H t D Ε H Ε J Ε           Ε H H Ε (Ε H)        −  = − 

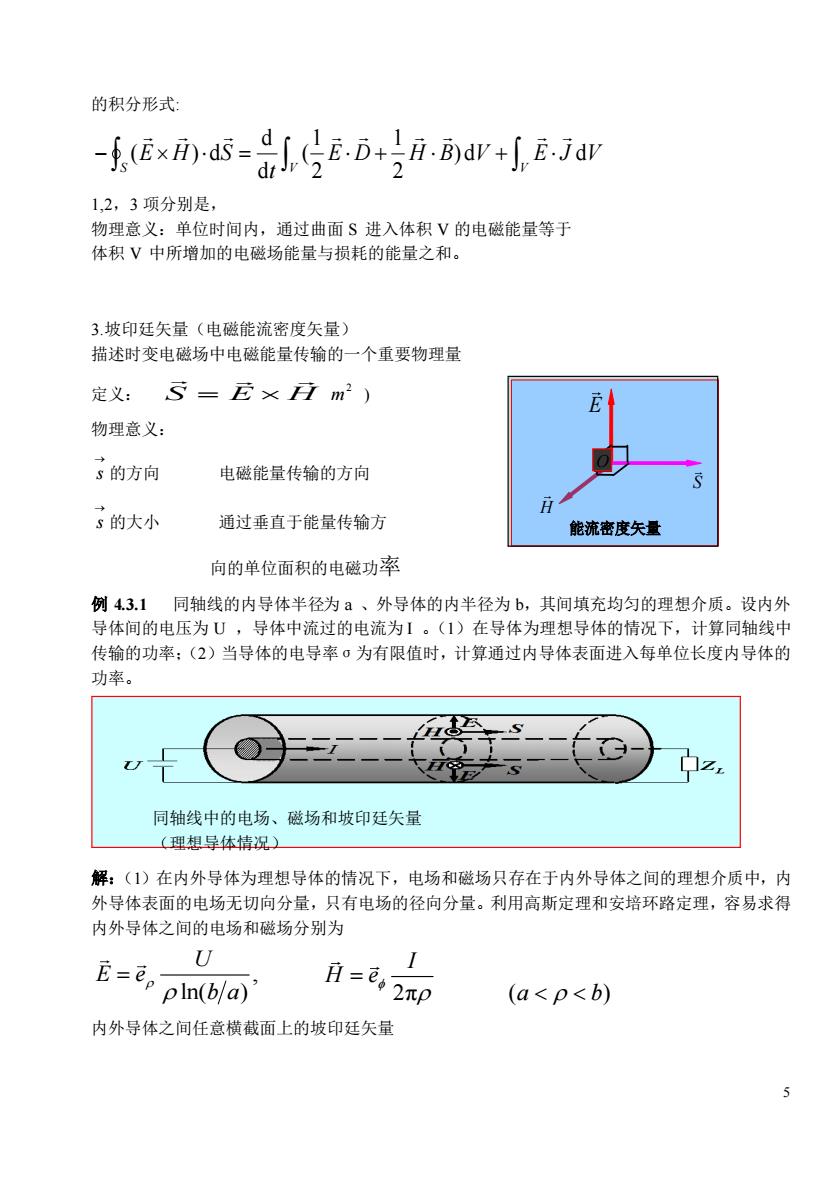
的积分形式 -f (ExH)-dS=d[(E.D+H.Bdv+[E.Jdv 12,3项分别是， 物理意义：单位时间内，通过曲面S进入体积V的电磁能量等于 体积V中所增加的电磁场能量与损耗的能量之和。 3.坡印廷矢量（电磁能流密度矢量） 描述时变电磁场中电磁能量传输的一个重要物理量 定义：5=E×方m2) 物理意义： 3的方向 电磁能量传输的方向 S的大小 通过垂直于能量传输方 能流密度矢量 向的单位面积的电磁功率 例43.1同轴线的内导体半径为a、外导体的内半径为b,其间填充均匀的理想介质。设内外 导体间的电压为U，导体中流过的电流为。(1)在导体为理想导体的情况下，计算同轴线中 传输的功率：(2)当导体的电导率σ为有限值时，计算通过内导体表面进入每单位长度内导体的 功率。 同轴线中的电场、磁场和坡印廷矢量 (理想导体情况) 解：(1)在内外导体为理想导体的情况下，电场和磁场只存在于内外导体之间的理想介质中，内 外导体表面的电场无切向分量，只有电场的径向分量。利用高斯定理和安培环路定理，容易求得 内外导体之间的电场和磁场分别为 U E=2 pin(bla) i=色，2p (a<p<b) 内外导体之间任意横截面上的坡印廷矢量

5 的积分形式:    −   =  +  +  S V V E D H B V E J V t E H S )d d 2 1 2 1 ( d d ( ) d          1,2，3 项分别是， 物理意义：单位时间内，通过曲面 S 进入体积 V 的电磁能量等于 体积 V 中所增加的电磁场能量与损耗的能量之和。 3.坡印廷矢量（电磁能流密度矢量） 描述时变电磁场中电磁能量传输的一个重要物理量 定义： ( W/ 2 m ) 物理意义： → s 的方向 电磁能量传输的方向 → s 的大小 通过垂直于能量传输方 向的单位面积的电磁功率 例 4.3.1 同轴线的内导体半径为 a 、外导体的内半径为 b，其间填充均匀的理想介质。设内外 导体间的电压为 U ，导体中流过的电流为 I 。（1）在导体为理想导体的情况下，计算同轴线中 传输的功率；（2）当导体的电导率σ为有限值时，计算通过内导体表面进入每单位长度内导体的 功率。 解：（1）在内外导体为理想导体的情况下，电场和磁场只存在于内外导体之间的理想介质中，内 外导体表面的电场无切向分量，只有电场的径向分量。利用高斯定理和安培环路定理，容易求得 内外导体之间的电场和磁场分别为 , ln( ) U E e b a   = 2π I H e  = ( ) a b    内外导体之间任意横截面上的坡印廷矢量 同轴线中的电场、磁场和坡印廷矢量 （理想导体情况） S Ε H    =  H S 能流密度矢量 E O