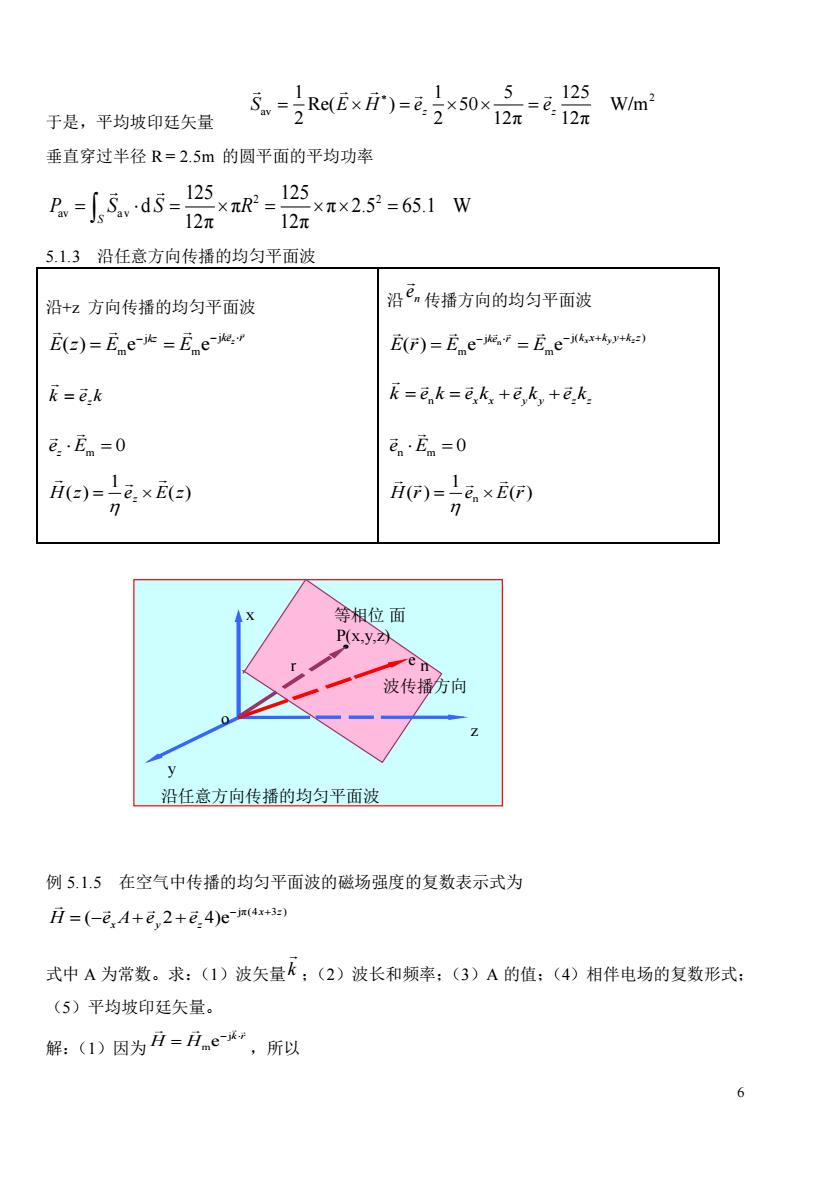
于是,平均坡印廷矢量 垂直穿过半径R=2.5m的圆平面的平均功率 g-5 ×π×2.52=65.1W 5.1.3沿任意方向传播的均匀平面波 沿+z方向传播的均匀平面波 沿传播方向的均匀平面波 E(=)=Ee-=Eewe.r E(F)=Eer=Ee5we k=ik k=ik=@k,+8ky+e.k e.Em =0 en·En=0 ie-xe) G)=e×E 等相位面 yxy,2头 波传播方向 沿任意方向传播的均匀平面波 例5.1.5在空气中传播的均匀平面波的磁场强度的复数表示式为 月=(-eA+e,2+e,4)e4 式中A为常数。求:(1)波矢量k:(2)波长和频率:(3)A的值:(4)相伴电场的复数形式: (5)平均坡印廷矢量。 解:()因为i=月.e”,所以
6 于是,平均坡印廷矢量 2 av 1 1 5 125 Re( ) 50 W/m 2 2 12π 12π z z S E H e e = = = 垂直穿过半径 R = 2.5m 的圆平面的平均功率 2 2 av a v 125 125 d π π 2.5 65.1 W S 12π 12π P S S R = = = = 5.1.3 沿任意方向传播的均匀平面波 沿+z 方向传播的均匀平面波 j j m m ( ) e e z kz ke r E z E E − − = = k e kz = e E z = m 0 ( ) 1 H(z) e E z z = 沿 n e 传播方向的均匀平面波 n j j( ) m m ( ) e e x y z ke r k x k y k z E r E E − − + + = = n x x y y z z k e k e k e k e k = = + + e E n m = 0 n 1 H r e E r ( ) ( ) = 例 5.1.5 在空气中传播的均匀平面波的磁场强度的复数表示式为 jπ(4 3 ) ( 2 4)e x z H e A e e x y z − + = − + + 式中 A 为常数。求:(1)波矢量 k ;(2)波长和频率;(3)A 的值;(4)相伴电场的复数形式; (5)平均坡印廷矢量。 解:(1)因为 j m e k r H H − = ,所以 沿任意方向传播的均匀平面波 波传播方向 z y x o r n e 等相位 面 P(x,y,z)

H=-@+2+e.4,k.F=kx+k y+k=4x+3 则k=4红、k,=0、k=3元,k=E,4红+E3π k=V(3π)2+(4π)}2=5元 。=反=已3+e3 1=2红-2红2 =7.5×10Hz (2) 3)K-月。=4-A0+0x2+3×4=0→,A=3 (4)E=nir)x元 =120m-e,3+,2+元4lem×尼号+e =120π(色,1.2+e5-1.6)e-4x+) 5=RelEx] =2Re120e,1.2+e,5-1.60e ×(-E,3+E,2+E4)em4*3:} (5) =12元×29×(e,4+e3)W/m2 5.2电磁波的极化 5.2.1极化的概念 5.2.2 线极化波 5.2.3 圆极化波 5.2.4 椭圆极化波 5.2.5 极化波的分解 5.2.6 极化波的工程应用 5.2.1极化的概念 波的极化在电磁波传播空间给定点处,电场强度矢量的端点随时间变化的轨迹。 波的极化表征在空间给定点上电场强度矢量的取向随时间变化的特性,是电磁理论中的一个重 要概念。 极化的三种形式 一般情况下,沿+:方向传播的均匀平面波E=E,E+,E,其中 E =E cos(ot-k+d),E=Eym cos(t-+)
7 m 2 4 H e e e = − + + x y z ,k r k x k y k z x z = + + = + x y z 4π 3π 则 4π 0 3π x y z k k k = = = 、 、 ,k e e = + x z 4π 3π 2 2 k = + = (3π) (4π) 5π n 4 3 x z 5 5 k e e e k = = + (2) 2π 2π 2 m k 5π 5 === , 7.5 10 Hz 2 / 5 3 10 8 8 = = = c f (3) m k H A = − + + = 4π( ) 0 2 3π 4 0 , A = 3 (4) 0 n E r H r e ( ) ( ) = jπ(4 3 ) jπ(4 3 ) 4 3 120π( 3 2 4)e ( ) 5 5 120π( 1.2 5 1.6)e x z x y z x z x z x y z e e e e e e e e − + − + = − + + + = + − (5) * av jπ (4 3 ) jπ (4 3 ) * 2 1 Re[ ] 2 1 Re 120π( 1.2 5 1.6)e 2 [( 3 2 4)e ] 12π 29 ( 4 3) W m x z x y z x z x y z x z S E H e e e e e e e e − + − + = = + − − + + = + 5.2 电磁波的极化 5.2.1 极化的概念 5.2.2 线极化波 5.2.3 圆极化波 5.2.4 椭圆极化波 5.2.5 极化波的分解 5.2.6 极化波的工程应用 5.2.1 极化的概念 波的极化 在电磁波传播空间给定点处,电场强度矢量的端点随时间变化的轨迹。 波的极化表征在空间给定点上电场强度矢量的取向随时间变化的特性, 是电磁理论中的一个重 要概念。 极化的三种形式 一般情况下,沿 + z 方向传播的均匀平面波 x x yEy E e E e = + ,其中 m cos( ) , E E t kz x x x = − + m cos( ) E E t kz y y y = − +

电磁波的极化状态取决于E,和B,的振幅之间和相位之间的关系,分为:线极化、圆极化、 椭圆极化。 线极化:电场强度矢量的端点轨迹为一直线段 圆极化:电场强度矢量的端点轨迹为一个圆 椭圆极化:电场强度矢量的端点轨迹为一个椭圆 5.2.2线极化波 条件:攻-月=0or±π 合成波电场的模 E=√E0,)+E0,)=√E+Ecos(o1+4)+-" 随时间变化 合成波电场与+x轴的夹角 a=arctan( E)=±arctan( 一一常数 Em 特点:合成波电场的大小随时间变化但其矢端,轨迹与x轴的夹角始终保持不变 结论:任何两个同频率、同传播方向且极化方向互相垂直的线极化波,当它们的相位相同或相差 为士π时,其合成波为线极化波。 5.2.3圆极化波 条件 Em=Em=Em、4-4,=±π/2 则E,(0,)=Ecos(o1+4) 常数 E,(0,0=Ecos(o1+只于7=±E.sin(or+) 随时间变化 合成波电场的模 E=NE(0,)+E(0,)=E.4 合成波电场与+x轴的夹角 a=arctan[±tan(ot+,】=±(oi+g.) 特点:合成波电场的大小不随时间改变,但方向却随时间变化,电场的矢端在一个圆上并以角速 度0旋转。 结论:任何两个同频率、同传播方向且极化方向互相垂直的线极化波,当它们的振幅相同、相位 差为士12时,其合成波为圆极化波。 右旋圆极化波:若鸟-项=一x/2 则电场矢端的旋转方向与电磁波传播方向成右手螺旋关系, 称为右旋圆极化波 左旋圆极化波:若4=2,则电场矢端的旋转方向电磁波传播方向成左手螺旋关系,称 为左旋圆极化波
8 电磁波的极化状态取决于 Ex 和 Ey 的振幅之间和相位之间的关系,分为:线极化、圆极化、 椭圆极化。 线极化:电场强度矢量的端点轨迹为一直线段 圆极化:电场强度矢量的端点轨迹为一个圆 椭圆极化:电场强度矢量的端点轨迹为一个椭圆 5.2.2 线极化波 条件: x − y = 0 or 合成波电场的模 2 2 2 2 m m (0, ) (0, ) cos( ) E E t E t E E t = + = + + x y x y x 合成波电场与+ x 轴的夹角 m m arctan( ) arctan( ) y y x x E E E E = = 特点:合成波电场的大小随时间变化但其矢端,轨 迹与 x 轴的夹角始终保持不变 结论:任何两个同频率、同传播方向且极化方向互相垂直的线极化波,当它们的相位相同或相差 为±π时,其合成波为线极化波。 5.2.3 圆极化波 条件 m m m π / 2 E E E x y x y = = − = 、 则 m (0, ) cos( ) E t E t x x = + m π (0, ) cos( ) sin( ) 2 E t E t E t y x m x = + = + 合成波电场的模 2 2 m (0, ) (0, ) E E t E t E = + = x y 合成波电场与+ x 轴的夹角 arctan[ tan( )] ( ) x x = + = + t t 特点:合成波电场的大小不随时间改变,但方向却随时间变化,电场的矢端在一个圆上并以角速 度ω 旋转。 结论:任何两个同频率、同传播方向且极化方向互相垂直的线极化波,当它们的振幅相同、相位 差为±π/ 2 时,其合成波为圆极化波。 右旋圆极化波:若 y −x = − 2 ,则电场矢端的旋转方向与电磁波传播方向成右手螺旋关系, 称为右旋圆极化波 左旋圆极化波:若 y −x = 2 ,则电场矢端的旋转方向电磁波传播方向成左手螺旋关系,称 为左旋圆极化波。 随时间变化 常数 常数 随时间变化