
要 一级反应半衰期与反应速率常数成反比,与反应物初始浓度无关,给定反应,是个常数。 反应物消耗34所需时间:寻=n云 一级反应的分数寿期均与反应物初始浓度无关,给定反应下是一个常数。 讨论一级反应的特点 1.lC对t作图是一直线,其斜率等于速率常数的负值(见图9-2-1)。 图9-21一级反应的nc图 2k的单位是[时间,S,min,h 1反应当反应浓度降为始浓度的1%时需时若将反应物起始浓度提高二 加快反应速度,当反应物浓度降为起始浓度1%时,需时5,则 【>【 t=【 【<【 1414 例2:C可存在于有生命的树木中,C放射性蚁变的:6665730年,测得一个考古样里仍含 有生命树木72%C”的木质,问考古样距今有多少年? 解:K=K=子n 四.二级反应(Second order reaction 凡是 的浓度的平方(减两种物质浓度的乘积)成正比的反应称为二级 如酯化,硝化等反应都是二级反应。 当cc时,k(9-2-10) 若总反应式为 A+B即与 0 a-X 以产物的生成速率表示反应速率,则
t = = (9-2-8) 一级反应半衰期与反应速率常数成反比,与反应物初始浓度无关,给定反应,是个常数。 反应物消耗3/4所需时间t = Ln 一级反应的分数寿期均与反应物初始浓度无关,给定反应下是一个常数。 讨论一级反应的特点 1.lnC对t作图是一直线,其斜率等于速率常数的负值(见图9-2-1)。 图9-2-1一级反应的ln-c图 2.k 1的单位是[时间] -1 ,S -1 , min -1 ,h -1 。 3.t 与初始浓度无关,仅与K 1 成反比, 一定反应为常数,其它分数寿期也一样。同一反应,不管初始浓度为多少,只要达到相同的转化率,则所需要的时间都是一样的。 例1:某一级反应,当反应浓度降为起始浓度的1%时,需时t 1 s若将反应物起始浓度提高一倍, 加快反应速度,当反应物浓度降为起始浓度1%时,需时t 2 s, 则 t 1 > t 2 t 1 = t 2 t 1 < t 2 某化学反应其反应消耗3/4所需时间使它消耗1/2所需时间的2倍,则反应为 0 1 2 3 级 一级反应的一种重要的用途就是测定矿石年龄和考古样品的年代 例2:C可存在于有生命的树木中, C放射性蜕变的t 1/2 =5730年,测得一个考古样里仍含 有生命树木72% C 14 的木质,问考古样距今有多少年? 解:K 1 = K 1 = Ln K 1 = = =1.209×10 -4 年 -1 T= = =2714年 四.二级反应(Second order reaction) 凡是反应速率与反应物的浓度的平方(或两种物质浓度的乘积)成正比的反应称为二级 反应。二级反应较普遍,大部分有机反应,如酯化,硝化等反应都是二级反应。 二级反应速率方程式为:r=k 2 c A c B (9-2-9) 当c A =c B 时,r=k 2 c 2 (9-2-10) 若总反应式为 A +BP t=0 a b 0 t a-x b-x x 以产物P的生成速率表示反应速率,则有

r音-kaxb-9(9-2山 设A和B的起始浓度相等,即ab,则上式化为 面=k(ax) 移项积分 a奇=k,h 六-是=k (9-2-12) aix)=kl k=a-可(9-2.13) 若令y代表t时刻,原始反应物已分解的分数 v=d k=ia(9-2.14) 当Y=12时,即原始反应物消耗一半时, (=a (9-2-15) 级反应的半衰期与起始浓度成反比。对于相同的转化率,如果初始浓度减半,时间 1,以立对作图应得一直线,直线的斜率等于速率常数k,k的单位通常为 dm·mol·s 2.二级反应的半衰期与起始浓度成反比。这可作为判断二级反应的依据。 当ab时,其速率方程式为 鲁kexb 移项得 a-c-可=k,dl 积分 at-西=k,dl 左边:会【六h=6 =六血÷-ln).六h8别 故郁÷血哥 (9-2-16) 以血号对作图可得一直线,由其斜率可求得速率常数,的值。K的单位为mm0g 对这种情况,不提半衰期。 五三级反应(third order reaction) 凡是应速 与反应物浓度的三次方(或三种浓度的乘积)成正比的反应,称为三级 反应。三级反应可有下列三种类型. 1)3AP> 2)2A+B-→P 3)A+B+CP→
r= =k 2 (a-x)(b-x) (9-2-11) 设A和B的起始浓度相等,即a=b,则上式化为 =k 2 (a-x) 2 移项积分 (9-2-12) 或 k 2 = (9-2-13) 若令y代表t时刻,原始反应物已分解的分数 y= k 2 = (9-2-14) 当Y=1/2时,即原始反应物消耗一半时, (9-2-15) 二级反应的半衰期与起始浓度成反比。对于相同的转化率,如果初始浓度减半,时间 加倍,这是二级反应的特征。 讨论: 1.以 对t作图应得一直线 ,直线的斜率等于速率常数k 2 ,k 2 的单位通常为 dm 3 ·mol -1 ·s -1 。 2. 二级反应的半衰期与起始浓度成反比。这可作为判断二级反应的依据。 当ab时,其速率方程式为 =k 2 (a-x)(b-x) 移项得 积分 左边= = = = 故有k 2 t= (9-2-16) 或k 2 t= + (9-2-17) 以 对t作图可得一直线,由其斜率可求得速率常数k 2 的值。K 2 的单位为dm 3 ·mol -1 ·s -1 。 对这种情况,不提半衰期。 五.三级反应(third order reaction) 凡是反应速率与反应物浓度的三次方(或三种浓度的乘积)成正比的反应,称为三级 反应。三级反应可有下列三种类型. 1)3AP 2)2A+B→ P 3)A+B+CP

仅讨论最简单的一种情况,即第三种类型。 A+B CP 0 a-x b-x c-x x 速率方程为 鲁=k(axb-xe-9(92-18) 当a=b-c时,上式化为 鲁=ka29-219 k=女中)9-220 k的量纲为[浓度]2.[时间] 其半衰期 三级反应较少见尤其在气相反应中更少见现已知的仅有5个这些反应都与NO有关 2NO+H. NO+HO 2NO+O NO. 2NO+CI 2NOCI 2NO+Br, 2NOBr 2NO+D. N20+D,0 ction 动力学速率方程为=.帝大(92-21) 移项积分得:c=k,+B 当t=0时c=c 故c=k+6。(9222) 当c=2时,可得半衰期与起始浓度成正比 t 季级反应的 征 字袋的半期与初始物浓度成正比,与反应速率常数,成反比:以c对作图得一直 线,其斜率即为k 例如NH在W丝上分解,一些皂化反应和异相催化反应。对于某一个参加反应的物质而言, 表9-2-1简单反应的速率方程及半衰期 级反应式 起始浓度条件 速率公式 积分式 半衰 数 期 零A→产物 CA.0=a -=k cA=a-kpl 级 A→产物 CA.0=Q -=kCA Inca=Ina-kt
仅讨论最简单的一种情况,即第三种类型。 A+ B+ CP t=0 a b c 0 t a-x b-x c-x x 速率方程为 =k 3 (a-x)(b-x)(c-x) (9-2-18) 当a=b=c时,上式化为 =k 3 (a-x) 3 (9-2-19) 移项积分得 = k 3 = ) (9-2-20) k 3 的量纲为[浓度] -2 ·[时间] -1 其半衰期t = 三级反应较少见,尤其在气相反应中更少见,现已知的仅有5个,这些反应都与NO有关. 2NO + H 2 N 2 O + H 2 O 2NO + O 2 NO 2 2NO + Cl 2 2NOCl 2NO + Br 2 2NOBr 2NO + D 2 N2O + D 2 O 六. 零级反应(zero order reaction) 反应速率与参加反应的物质浓度无关时称为零级反应。 动力学速率方程为r=- =k 0 (9-2-21) 移项积分得:c=-k 0 t+B 当t=0时c=c 0 故c=-k 0 t+ c 0 (9-2-22) 当c= 时,可得半衰期与起始浓度成正比 t = (7-2-23) 零级反应的特征: 零级反应的半衰期与初始物浓度成正比,与反应速率常数k 0成反比;以c对t作图得一直 线,其斜率即为-k 0。 例如NH 3在W丝上分解,一些皂化反应和异相催化反应。对于某一个参加反应的物质而言, 级数是零的反应是常见的。 以上讨论了几种具有简单级数的反应的速率方程式,现将有关公式列于表7-2-1。 表9-2-1简单反应的速率方程及半衰期 级 数 反应式 起始浓度条件 速率公式 积分式 半衰 期 零 级 一 级

A+B→产物CA0=Ca.0=Q -号=k,c24=+k10 级 +B+C→产物C%n=C0=Ce0=a-号=k04c9e之=+2kg 93反应级数的确定 在动力学研究中,我们先要建立其动力学方程式,常见的动力学方程形式为.等C ”·C.,一反应如果各反应物级数确定了,则可以确定动力学方程。如何由实验上测 得不同时刻的浓度,确定反应级数,对于建立动力学方程是至关重要的一步。这一节就来讨 论这个问题。 一.微分法(differential method) 设一反应A一→P,其速率方程为kC”,测出c曲线(见图93-1),曲线上任一点的切 线,就是该浓度下的瞬时速度。 图931反应物浓度对时间的关系 当反应物浓度为c时,=kc,,当反应物浓度为c,时,【,k。 将二式分别取对数Lgr,=Lgk+nlgc Lgr,=Lgk+nLgc 授 ,即可求出n Lgc作图得直线(见图9-3-2),直线 的斜率 为反应级数n。 图9-3-2 这种处理方法特点是在©-t图上,测出不同时刻的斜率,时间是不相同的,这种方法求 的级数称为对时间而言的级数。 2.起始速率法
二 级 三 级 9-3反应级数的确定 在动力学研究中,我们先要建立其动力学方程式,常见的动力学方程形式为- =kC A α ·C B β .,一反应如果各反应物级数确定了,则可以确定动力学方程。如何由实验上测 得不同时刻的浓度,确定反应级数,对于建立动力学方程是至关重要的一步。这一节就来讨 论这个问题。 一. 微分法(differential method) 所谓微分法就是用速率公式的微分形式来确定反应级数的方法。 1. 图解微分法 设一反应A→ P,其速率方程为r=kC n ,测出c–t曲线(见图9-3-1),曲线上任一点的切 线,就是该浓度下的瞬时速度。 图9-3-1 反应物浓度对时间的关系 当反应物浓度为c 1 时,r 1 =kc 1 n ,当反应物浓度为c 2 时,r 2 =kc 2 n 将二式分别取对数Lgr 1 =Lgk +nLgc 1 Lgr 2 =Lgk +nLgc 2 n= 只要求得曲线上任意两浓度下的速率,即可求出n。 也可以对速率公式通式取对数Lgr=nLgc + Lgk,用Lgr对Lgc作图得直线(见图9-3-2),直线 的斜率即为反应级数n。 图9-3-2 这种处理方法特点是在c –t图上,测出不同时刻的斜率,时间是不相同的,这种方法求 的级数称为对时间而言的级数。 2. 起始速率法
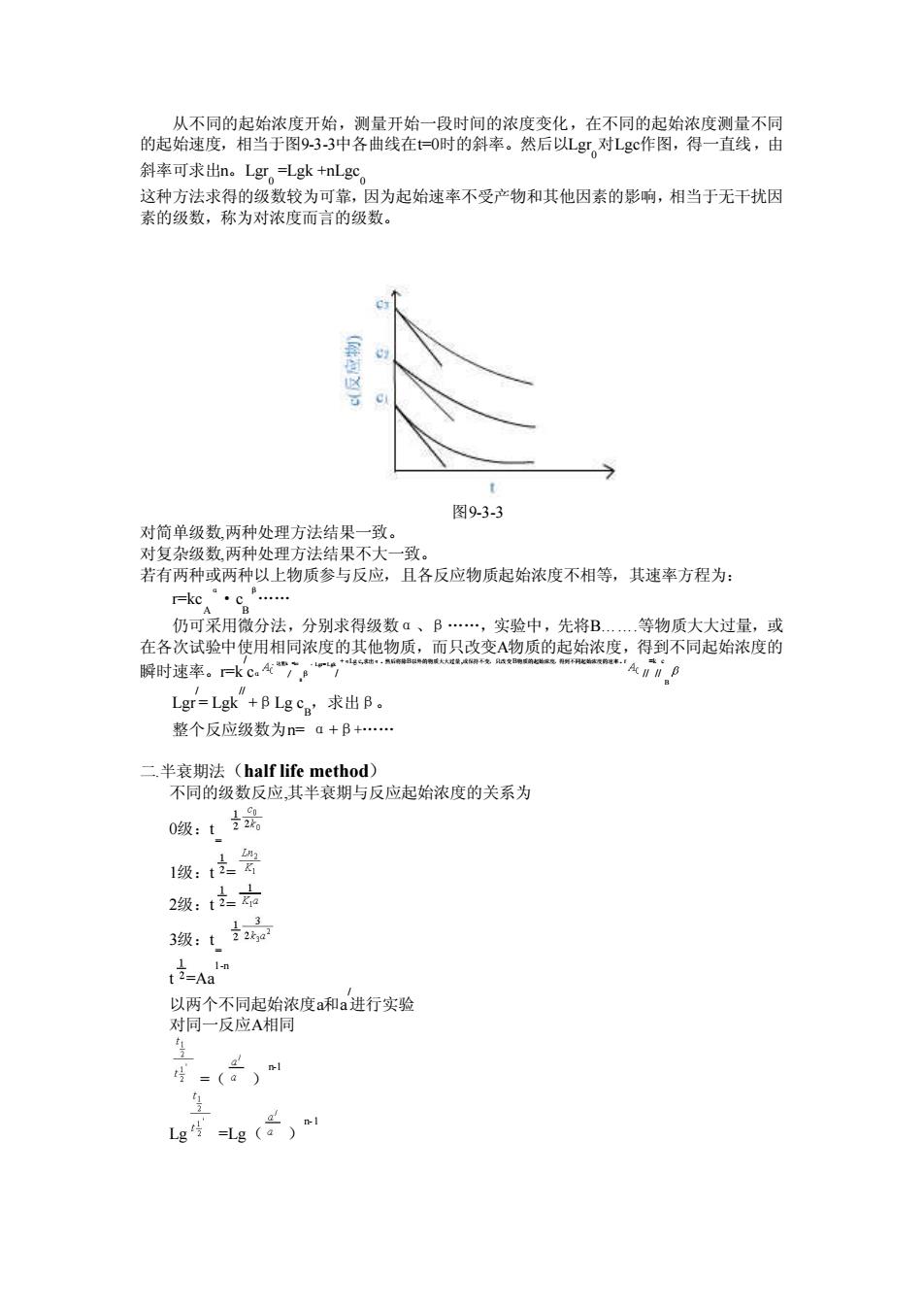
从不同的起始浓度开始,测量开始一段时间的浓度变化,在不同的起始浓度测量不同 的起始速度,相当于图933中各曲线在O时的斜率。然后Lg对Lgc作图,得一直线,由 斜率可求出n。Lgr=Lgk+nLg9 数较为可靠 ]为起始速率不受产物和其他因素的影响,相当于无干扰因 图933 对简单级数,两种处理方法结果一致。 对复杂级数,两种处理方法结果不大一致。 若有两种或两种以上物质参与反应,且各反应物质起始浓度不相等,其速率方程为: 仍可采用微分法,分别求得级数a、B.实验中,先将B. 物质大大付量,或 在各次试验中使用相同浓度的其他物质,而只变A物质的起始浓度,得到不同起始浓度的 解时速率。k4。 Lg=Lg“+BLgg求出B, 整个反应级数为na+B+ thod 0级:1品 1级:支之 2级:t这 3级:动 t之=A阳 =() Lgg)
从不同的起始浓度开始,测量开始一段时间的浓度变化,在不同的起始浓度测量不同 的起始速度,相当于图9-3-3中各曲线在t=0时的斜率。然后以Lgr 0 对Lgc作图,得一直线,由 斜率可求出n。Lgr 0 =Lgk +nLgc 0 这种方法求得的级数较为可靠,因为起始速率不受产物和其他因素的影响,相当于无干扰因 素的级数,称为对浓度而言的级数。 图9-3-3 对简单级数,两种处理方法结果一致。 对复杂级数,两种处理方法结果不大一致。 若有两种或两种以上物质参与反应,且各反应物质起始浓度不相等,其速率方程为: r=kc A α·c B β. 仍可采用微分法,分别求得级数α、β.,实验中,先将B. . .等物质大大过量,或 在各次试验中使用相同浓度的其他物质,而只改变A物质的起始浓度,得到不同起始浓度的 瞬时速率。r=k / cα ,这里k / =kc B β ,Lgr= Lgk / +αLg c,求出α。然后将除B以外的物质大大过量,或保持不变,只改变B物质的起始浓度,得到不同起始浓度的速率。r // =k // c B Lgr / = Lgk // +βLg c B,求出β。 整个反应级数为n= α+β+. 二.半衰期法(half life method) 不同的级数反应,其半衰期与反应起始浓度的关系为 0级:t = 1级:t = 2级:t = 3级:t = t =Aa 1-n 以两个不同起始浓度a和a / 进行实验 对同一反应A相同 =( ) n-1 Lg =Lg( ) n-1