
2021/9/17 弹性变形 ·对于剪切应变 =是 其中G为剪切模量或刚性模量 ·对于各向同性的无机材料,G、E和μ存在下面的关系 c-21+m ·体积变化模量K:在等静压P作用下,压力P与体积变化的 比值 k=品-32D-3a20 弹性变形 ·对于各向异性的材料,B≠B,≠B,≠≠4 ·假设受到正应力c,的作用,那么在y和z两个方向的应变为 6n=-4g=8n0, x方向的应变如=爱=8 其中S=是,S1=一常、S=一气被称为弹性柔顺系数 ·在维应力的作用中应力和应变的关系通式为其中 =品in十8r0n十0十8n十Saw+8n 7
2021/9/17 7 • 对于剪切应变 弹性变形 其中G为剪切模量或刚性模量 • 对于各向同性的无机材料,G、E和存在下面的关系 • 体积变化模量K:在等静压P作用下,压力P与体积变化的 比值 • 对于各向异性的材料, • 假设受到正应力x的作用,那么在y和z两个方向的应变为 弹性变形 x方向的应变 其中 、 、 被称为弹性柔顺系数 • 在三维应力的作用下,应力和应变的关系通式为,其中 Sij=Sji

2021/9/17 弹性变形 ·由于S,S,独立的5,由36个缩减为21个 ·弹性系数为四阶张量,可根据晶体对称性进一步缩减 起出 a脱 Point group 6.6,6/m exagonal Point group 62,6mm,622,6/m 弹性变形 ·系技司不 三个独立的不为零的弹性柔顺系数 =8-2[(8u-3)-s(G+6+》 。=84+4[(8:-8e)-号8](阳+g+ 其中,1、,和l,位所考虑方向与<100>三个轴间的方向余弦 方向44 。0 ,/万/30 ,/万万万 ·可以算出上述三个方向的弹性和刚性模量不同一各向异性
2021/9/17 8 • 由于Sij=Sji,独立的Sij由36个缩减为21个 • 弹性系数为四阶张量,可根据晶体对称性进一步缩减 弹性变形 • MgO为立方晶系晶体,三个独立的不为零的弹性柔顺系数 S11、 S12和 S44 。可以证明任一方向: 弹性变形 其中l 1、l 2和l 3位所考虑方向与<100>三个轴间的方向余弦 • 可以算出上述三个方向的弹性和刚性模量不同—各向异性

2021/9/17 弹性变形 ·对于各向同性的材料,1/E与方向无关,即 ·因此(8-S)-28w=0 84=2(S1-S2) 8=2日+会-20 Su-G ·我们肉到0=十。 弹性模量 ·富性 个标志。 ·共价键、离子键结合的晶体, 结合力强,E都较大。分子 键结合力弱,这样键合的物 体E较低。 改变原子间距离将影响弹性 模量。压 子间距离 图1.原子闻的结合力 变小,曲线上 登力点的 增大,因而E将 9
2021/9/17 9 • 对于各向同性的材料,1/E与方向无关,即 弹性变形 • 因此 • 我们得到 • 与熔点、硬度类似,弹性模 量E是原子间结合强度的一 个标志。 • 弹性模量E实际上和原子间 结合力曲线上任 受力点的 弹性模量 结合力曲线上任一受力点的 曲线斜率有关。 • 共价键、离子键结合的晶体, 结合力强,E都较大。分子 键结合力弱,这样键合的物 体E较低。 • 改变原子间距离将影响弹性 模量。压应力使原子间距离 变小,曲线上该受力点的斜 率增大,因而E将增加;张应力 使原子间距离增加,因而E下 降

2021/9/17 复合材料的弹性模量 一些材料中存在着两相,其弹性模量可根据下述两个关系 进行估计: 一北十背群赞的西相应变相同,复合 品-虎+常 付是应力相同复合 ·E,和E,分别为第一相和第二相的弹性模量,V,和V,分别为 两相的体积分数,E,和E分别为复合材料弹性模量的上限 和下限。 复合材料的弹性模量 个 Isostrain Volume fraction→ A B 10
2021/9/17 10 • 一些材料中存在着两相,其弹性模量可根据下述两个关系 进行估计: 复合材料的弹性模量 并联模型 两相应变相同 复合 • E1和E2分别为第一相和第二相的弹性模量,V1和V2分别为 两相的体积分数,EU和EL分别为复合材料弹性模量的上限 并联模型,两相应变相同,复合 材料模量的上限 串联模型,两相应力相同,复合 材料模量的下限 两相的体积分数,EU和EL分别为复合材料弹性模量的上限 和下限。 E2 复合材料的弹性模量 A B Volume fraction → Ec → E1 E2 A Vf B
2021/9/17 多孔材料的弹性模量 对于含有气孔的材料,气孔 性 量为零的 密 一按公式计养的结果 面西爱经 一实验结果 B=B(1-1.9P+0.9P) 0.2 其中E为无气孔的材料的模 量,P为气孔率。 气孔率达50%仍可使用。如 果气孔变成连续相,偏差比 图1,6氧化铝相对弹性模量 较大。 与气孔率的关系 粘弹性和滞弹性 理想弹性 粘弹性 11
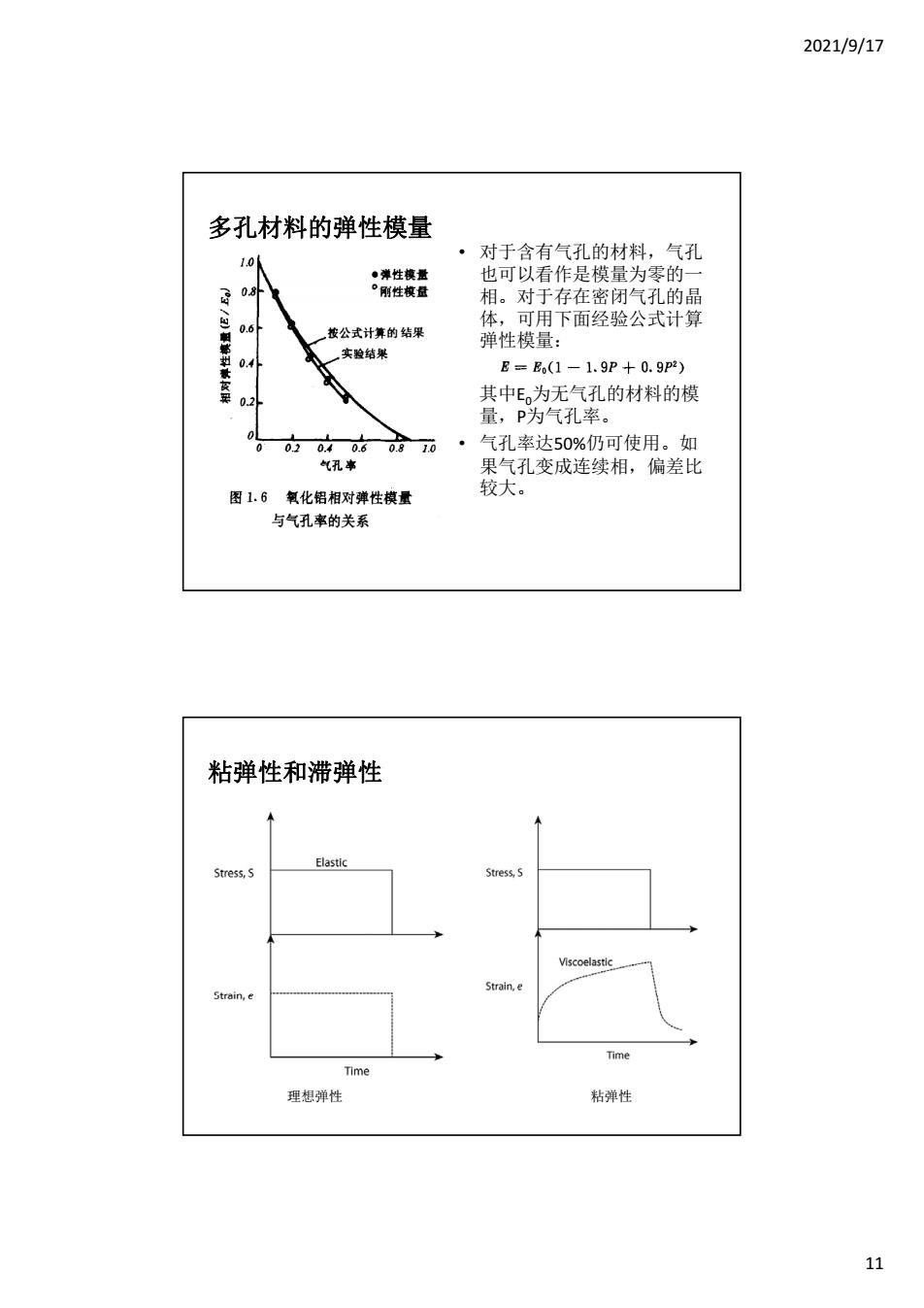
2021/9/17 11 • 对于含有气孔的材料,气孔 也可以看作是模量为零的一 相。对于存在密闭气孔的晶 体 可用下面经验公式计算 多孔材料的弹性模量 , 弹性模量: 其中E0为无气孔的材料的模 量,P为气孔率。 • 气孔率达50%仍可使用。如 果气孔变成连续相,偏差比 较大。 粘弹性和滞弹性 理想弹性 粘弹性