
MTSD@UPC 第一节价键理论 共振式(resonance》) 离子-共价共振,以HCI为例: ·若成键性质为纯共振,则有 Ψ=A(1)B(2)+A(2)B(1) ·不能描述离子键:两个电子全在CI(HC)或H(HCI+)上 ·离子键的成键波函数:Ψ=B(1)B(2)(H+C) ·体系波函数可写成共价波函数和离子波函数的叠加 平HC=亚H-q十入ΨHrC=亚covalent十入Ψionic ·共振式:对一种原子构型(原子核位置),将体系波函数写为几种不同 电子结构对应的波函数的叠加的形式 ·探测到离子型电子结构的几率正比于2 ·注意,共振式并非在不同电子结构间切换,而是量子叠加 2022/3/24 材料化学系:结构化学 11
MTSD@UPC 2022/3/24 材料化学系:结构化学 11 第一节 价键理论 共振式 (resonance) 离子-共价共振,以 HCl 为例: • 若成键性质为纯共振,则有 • 不能描述离子键:两个电子全在 Cl(H+Cl-) 或 H(H-Cl+)上 • 离子键的成键波函数:Ψ = 𝐵 1 𝐵(2) (H+Cl-) • 体系波函数可写成共价波函数和离子波函数的叠加 • 共振式:对一种原子构型(原子核位置),将体系波函数写为几种不同 电子结构对应的波函数的叠加的形式 • 探测到离子型电子结构的几率正比于𝜆 2 • 注意,共振式并非在不同电子结构间切换,而是量子叠加

MTSD@UPC 第一节价键理论 共振式(resonance》) 可利用变分原理(variation principle)求共振式中的参数入 变分原理:对于一给定体系,若使用任意一个(满足约束条件 的)波函数求体系能量(lamiltonian期望值),所得结果不低于 体系的真实能量。 试探波函数:一个满足约束条件的任意(近似)波函数 将求解Schrodinger方程的问题转换为数值优化问题(求最小值) 例:若某体系的波函数可写为如下形式:亚Hc=亚ovnlent十入亚ionic 已知该体系的能量最小值对应入=0.1,则描述该体系共振结构的波函数为 亚=亚covalent+0.1亚ionic 这表明若对该体系的成键性质进行测量,测得共价键和离子键的几率之比 为100:1。P402) 2022/3/24 材料化学系:结构化学 12
MTSD@UPC 2022/3/24 材料化学系:结构化学 12 第一节 价键理论 共振式 (resonance) 可利用变分原理(variation principle)求共振式中的参数 𝜆 变分原理:对于一给定体系,若使用任意一个(满足约束条件 的)波函数求体系能量(Hamiltonian期望值),所得结果不低于 体系的真实能量。 试探波函数:一个满足约束条件的任意(近似)波函数 将求解Schrödinger方程的问题转换为数值优化问题(求最小值) 例:若某体系的波函数可写为如下形式: 已知该体系的能量最小值对应 𝜆 = 0.1,则描述该体系共振结构的波函数为 这表明若对该体系的成键性质进行测量,测得共价键和离子键的几率之比 为100:1。(P402)

MTSD@UPC 第一节价键理论 共振式(resonance) 苯的共振式: C ·两个电子结构具有相同的能量 ·共振的效果:将单双键交替导致的电子分布不均抹平 ·共振波函数对应的电子结构具有更低的能量:resonance stabilization ·在VB理论中,共振稳定能解释了芳环的稳定性 ·可加入离子共价共振组份,使体系能量更低 2022/3/24 材料化学系:结构化学 13
MTSD@UPC 2022/3/24 材料化学系:结构化学 13 第一节 价键理论 共振式 (resonance) 苯的共振式: • 两个电子结构具有相同的能量 • 共振的效果:将单双键交替导致的电子分布不均抹平 • 共振波函数对应的电子结构具有更低的能量:resonance stabilization • 在VB理论中,共振稳定能解释了芳环的稳定性 • 可加入离子-共价共振组份,使体系能量更低
MTSD@UPC 第一节价键理论 杂化和活化 活化:将原子处于较低能量轨道的 H1s 电子激发至能量较高的轨道上: C:2s22p22p→2s12p22p32p2 H1s 02p C原子活化后则具有四个未成对电子 02p, 可与四个H原子形成四个σ键 H2O的成键: 能量: ·0:2s22p2p2p2 ·原子活化能量升高 ·两个H与O成键 ·形成更多化学键使能量降低 ·夹角90°? ·总效果使能量降低 ·其它问题:C可成4键 活化并非真实的物理过程 2022/3/24 材料化学系:结构化学 14
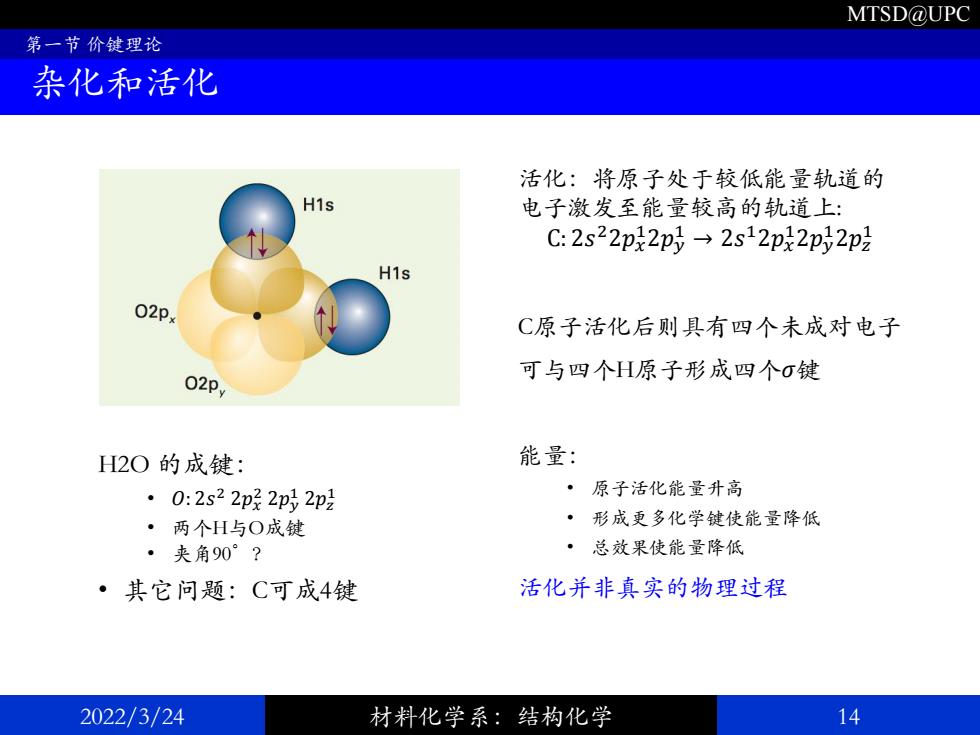
MTSD@UPC 2022/3/24 材料化学系:结构化学 14 第一节 价键理论 杂化和活化 H2O 的成键: • 𝑂: 2𝑠 2 2𝑝𝑥 2 2𝑝𝑦 1 2𝑝𝑧 1 • 两个H与O成键 • 夹角90°? • 其它问题:C可成4键 活化:将原子处于较低能量轨道的 电子激发至能量较高的轨道上: C: 2𝑠 22𝑝𝑥 12𝑝𝑦 1 → 2𝑠 12𝑝𝑥 12𝑝𝑦 12𝑝𝑧 1 C原子活化后则具有四个未成对电子 可与四个H原子形成四个𝜎键 能量: • 原子活化能量升高 • 形成更多化学键使能量降低 • 总效果使能量降低 活化并非真实的物理过程

MTSD@UPC 第一节价键理论 杂化和活化 ·C原子活化 2s22p22p→2s12p22p22p2 ·1个s电子,3个p电子←→CH中四个σ键相同 ·活化原子的四个轨道进一步杂化,形成杂化轨道 ·原来的四个轨道线性组合,形成杂化轨道 109.47° ·杂化轨道为四个原子轨道的相千叠加 ·四个杂化轨道正交 h1=s+pr十Py+pah2=s-px-pg十pe h3=s-px十pg-pzh4=s十pz-Pg-pz 验证C原子sp3杂化轨道的形式。 2022/3/24 材料化学系:结构化学 15
MTSD@UPC 2022/3/24 材料化学系:结构化学 15 第一节 价键理论 杂化和活化 • C原子活化 2𝑠 22𝑝𝑥 12𝑝𝑦 1 → 2𝑠 12𝑝𝑥 12𝑝𝑦 12𝑝𝑧 1 • 1个s电子,3个p电子 ➔ CH4中四个 𝜎 键相同 • 活化原子的四个轨道进一步杂化,形成杂化轨道 • 原来的四个轨道线性组合,形成杂化轨道 • 杂化轨道为四个原子轨道的相干叠加 • 四个杂化轨道正交 验证C原子sp3杂化轨道的形式