
MTSD@UPC 第一节价键理论 势能曲线和势能面 1.0800-11107.571 1.0825-11116.123 1.0850-11123.549 1.0875-11129.899 1.0900-11135.186 1.8925-11139.423 1.0950-11142.636 1.0975-11144.840 Internuclear 1.1000-11146.845 separation,R 1.1025-11146.289 D 1.1050-11145.588 1.1075-11143.955 大作业2:左侧数据为氮气分子在不同键长下的结合 1.1100-11141.409 能数据(左侧为键长,单位为A;左侧为结合能,单 1.1125-11137.981 位为meV)。用Morse势函数拟合此组结合能数据, 1.1150-11133.639 得出平衡键长及平衡位置时的结合能。 1.1175-11128.462 附加(选做):使用有限差分方法,求解一维自由粒 1.1200-11122.443 子、一维势箱、一维谐振子和上述一维Morse势下的 1.1225-11115.586 粒子的Schrodinger方程求解,并画出波函数及几率密 度分布。 2022/3/24 材料化学系:结构化学 6
MTSD@UPC 2022/3/24 材料化学系:结构化学 6 第一节 价键理论 势能曲线和势能面 大作业2:左侧数据为氮气分子在不同键长下的结合 能数据(左侧为键长,单位为Å;左侧为结合能,单 位为meV)。用Morse势函数拟合此组结合能数据, 得出平衡键长及平衡位置时的结合能。 附加(选做):使用有限差分方法,求解一维自由粒 子、一维势箱、一维谐振子和上述一维Morse势下的 粒子的Schrödinger 方程求解,并画出波函数及几率密 度分布

MTSD@UPC 第一节价键理论 双原子分子 最简单的分子:H2 ·若两个H原子相距很远,均处于基态,则体系的空间波函数为 Ψ(1,2)=X1s(r1)X1s.(r2) ·简记为Ψ(1,2)=A(1)B(2) ·若两原子靠近,两个电子可能在任意一个核周围,占据任一个轨道 ·有两种状态A(1)B(2)和A(2)B(1),且几率相等 ·Ψ(1,2)=A(1)B(2)±A(2)B(1)(为何第二项系数为±1?) ·两项同号(+)的情况体系具有更低的能量 ·价键波函数(空间部分)为: Ψ(1,2)=A(1)B(2)+A(2)B(1) ·在两原子核之间,两项呈相长千涉(constructive interference)),该区 域内电子几率分布增加 2022/3/24 材料化学系:结构化学 7
MTSD@UPC 最简单的分子: H2 • 若两个H原子相距很远,均处于基态,则体系的空间波函数为 • 简记为 Ψ 1,2 = 𝐴 1 𝐵(2) • 若两原子靠近,两个电子可能在任意一个核周围,占据任一个轨道 • 有两种状态 𝐴 1 𝐵 2 和 𝐴 2 𝐵(1),且几率相等 • Ψ 1,2 = 𝐴 1 𝐵 2 ± 𝐴 2 𝐵(1) (为何第二项系数为±1?) • 两项同号(+)的情况体系具有更低的能量 • 价键波函数(空间部分)为: • 在两原子核之间,两项呈相长干涉(constructive interference),该区 域内电子几率分布增加 2022/3/24 材料化学系:结构化学 7 第一节 价键理论 双原子分子

MTSD@UPC 第一节价键理论 双原子分子 例:写出H2分子价键波函数的完整形式。每个H原子的1s轨道参与 成键。 解:H原子的1s轨道波函数为:-e 1 代入H2分子的价键波函数表示式,有 Ψ(1,2)= (πad)pea/aX y (nad)1rze nlat (a)12ea。1 1 (nad)iz e/a Taeo+na+e+nay 1 练习:写出以上波函数在Cartesian坐标系 下的具体形式。其中A原子位于原点, e A A2 A-B键沿z轴正方向。P400) R A B 2022/3/24 材料化学系:结构化学 8
MTSD@UPC 例:写出H2分子价键波函数的完整形式。每个H原子的1s轨道参与 成键。 解:H原子的1s轨道波函数为: 代入H2分子的价键波函数表示式,有 2022/3/24 材料化学系:结构化学 8 第一节 价键理论 双原子分子 练习:写出以上波函数在Cartesian坐标系 下的具体形式。其中A原子位于原点, A-B键沿z轴正方向。(P400)

MTSD@UPC 第一节价键理论 共价键 H2分子的价键波函数如图 ·相对于原子核连线柱状对称 ·若沿对称轴看,类似于一个s轨道 A(1)B2) A(2)B1) ·→0键(希腊字母s) ·形成共价键的两个电子自旋配对 A(1)B(2)+A(2)B(1)Enhanced electron density 体系的总波函数为空间部分和自旋部分的乘积 Ψ(1,2)={A(1)B(2)+A(2)B(1)}σ(1,2) 由Paui原理,电子波函数相对于交换电子标号反对称: Ψ(2,1)={A(2)B(1)+A(1)B(2)}σ(2,1) ={A(1)B(2)+A(2)B(1)}σ(2,1) 则有σ(2,1)=-0(1,2),即自旋反平行 o-(1,2)=(1/212){a(1)3(2)-3(1)ax(2)} 2022/3/24 材料化学系:结构化学 9
MTSD@UPC 2022/3/24 材料化学系:结构化学 9 第一节 价键理论 共价键 体系的总波函数为空间部分和自旋部分的乘积 由Pauli原理,电子波函数相对于交换电子标号反对称: 则有 𝜎 2,1 = −𝜎(1,2),即自旋反平行 H2分子的价键波函数如图 • 相对于原子核连线柱状对称 • 若沿对称轴看,类似于一个s轨道 • ➔ 𝜎键 (希腊字母 s) • 形成共价键的两个电子自旋配对
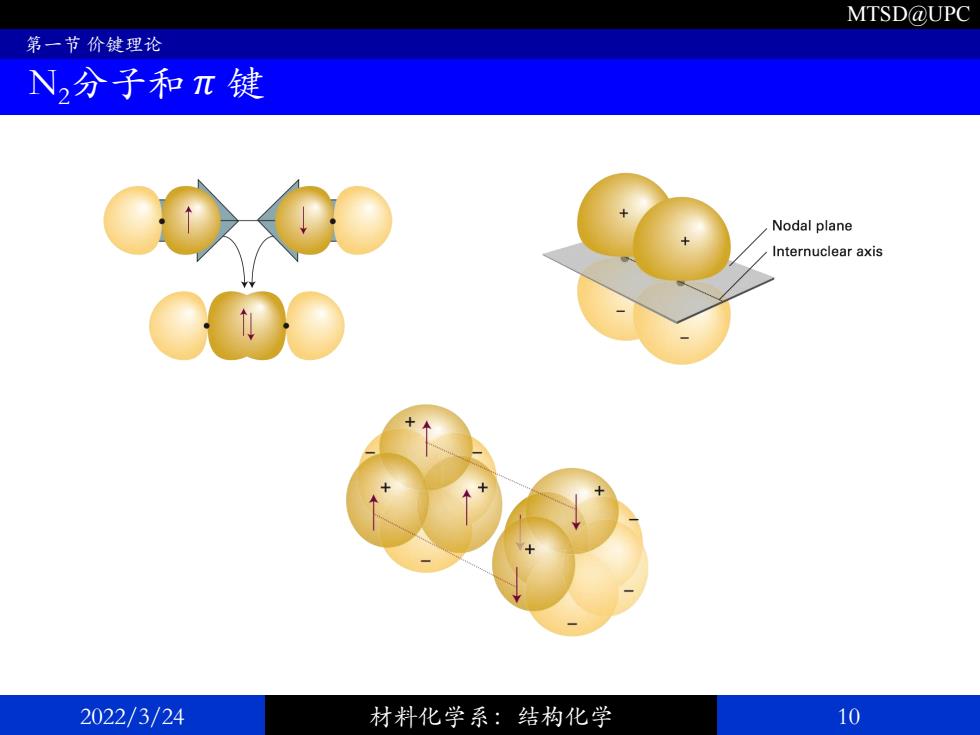
MTSD@UPC 第一节价键理论 N2分子和π键 Nodal plane Internuclear axis 2022/3/24 材料化学系:结构化学 10
MTSD@UPC 2022/3/24 材料化学系:结构化学 10 第一节 价键理论 N2分子和 𝜋 键