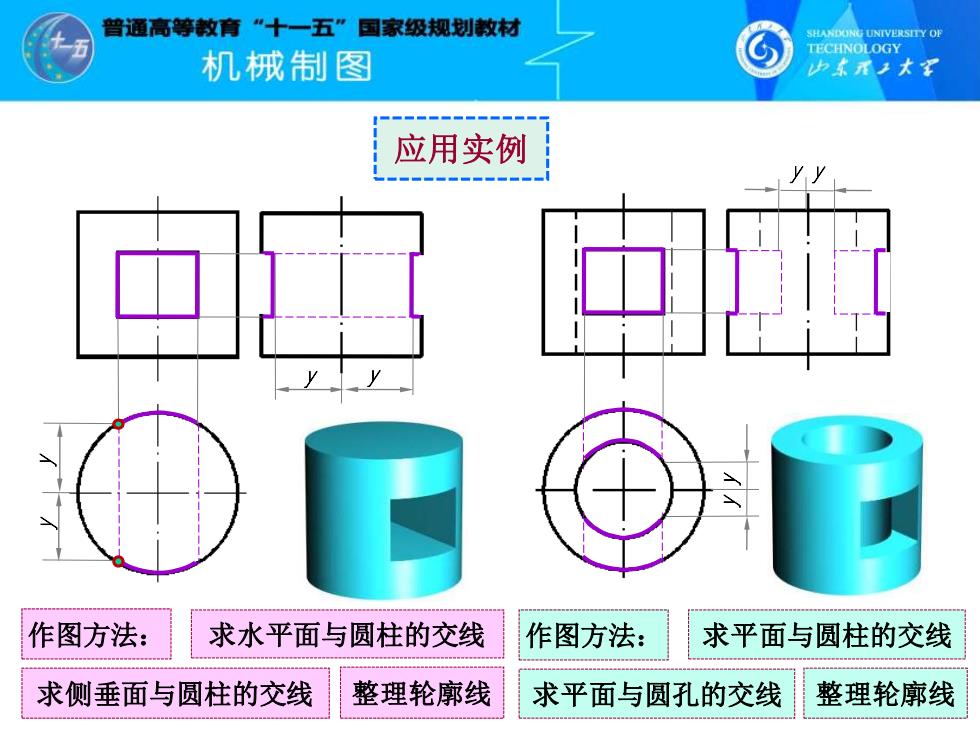
曾通高等教育”十一五”国家级规划教材 SHANDONG UNIVERSITY OF TECHNOLOGY 机饿制图 少东承子大军 应用实例 作图方法: 求水平面与圆柱的交线 作图方法: 求平面与圆柱的交线 求侧垂面与圆柱的交线 整理轮廓线 求平面与圆孔的交线 整理轮廓线
y y y y y y y y 作图方法: 求侧垂面与圆柱的交线 求水平面与圆柱的交线 整理轮廓线 作图方法: 求平面与圆孔的交线 求平面与圆柱的交线 整理轮廓线 应用实例
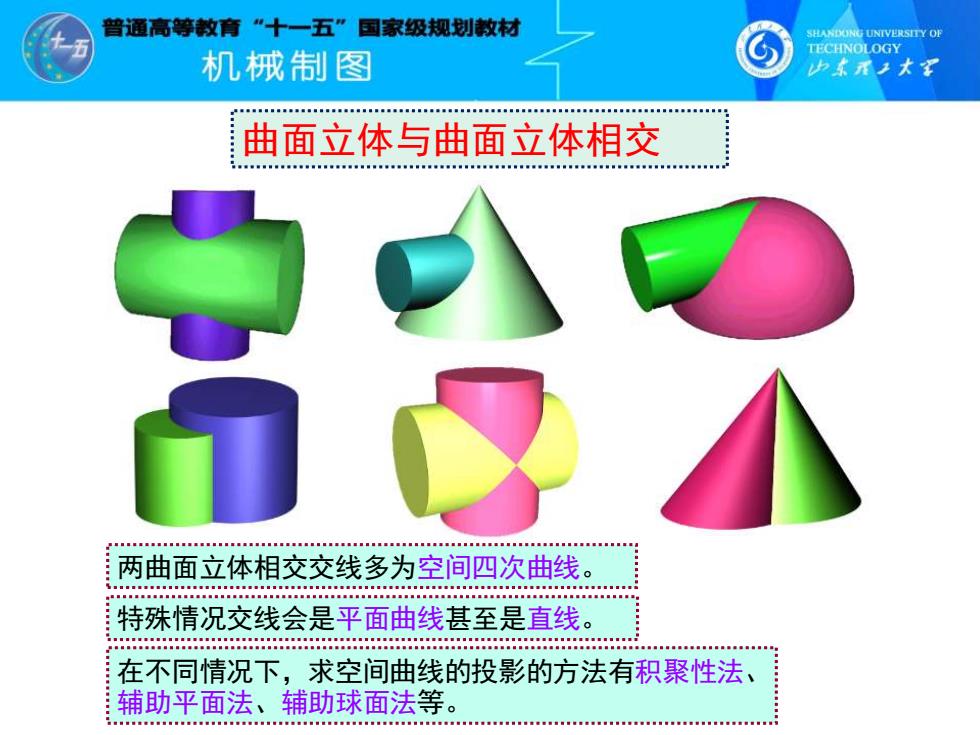
曾通高等教育“十一五”国家级规划敏材 SHANDONG UNIVERSITY OF TECHNOLOGY 机饿制图 少素承子大军 曲面立体与曲面立体相交 19000000n 两曲面立体相交交线多为空间四次曲线。 特殊情况交线会是平面曲线甚至是直线。 48 在不同情况下,求空间曲线的投影的方法有积聚性法、 辅助平面法、辅助球面法等。 EMMMEOOHHNEEE3E8MMB00BM353ME05536A35F653MMMAC83MAMN30ENN08AM5AA0M056AE364
曲面立体与曲面立体相交 两曲面立体相交交线多为空间四次曲线。 在不同情况下,求空间曲线的投影的方法有积聚性法、 辅助平面法、辅助球面法等。 特殊情况交线会是平面曲线甚至是直线
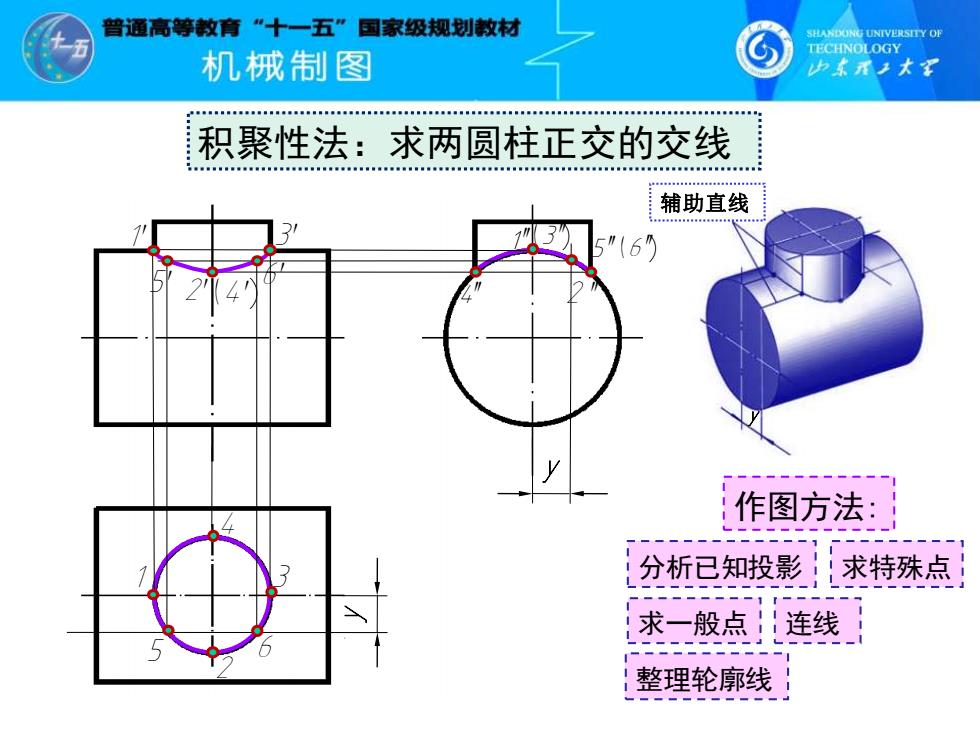
曾通高等教育”十一五”国家级规划教材 SHANDONG UNIVERSITY OF TECHNOLOGY 机饿制图 少东承2大军 积聚性法:求两圆柱正交的交线 辅助直线 "(6 作图方法:】 分析已知投影求特殊点 求一般点连线 整理轮廓线
积聚性法:求两圆柱正交的交线 1′ 3′ (4′) 4′′ 2 ′′ 2 1 作图方法: 求特殊点 求一般点 连线 整理轮廓线 分析已知投影 y y y 辅助直线 3 4 5 6 5′2′ 6′ 1′′(3′′) 5′′(6′′)
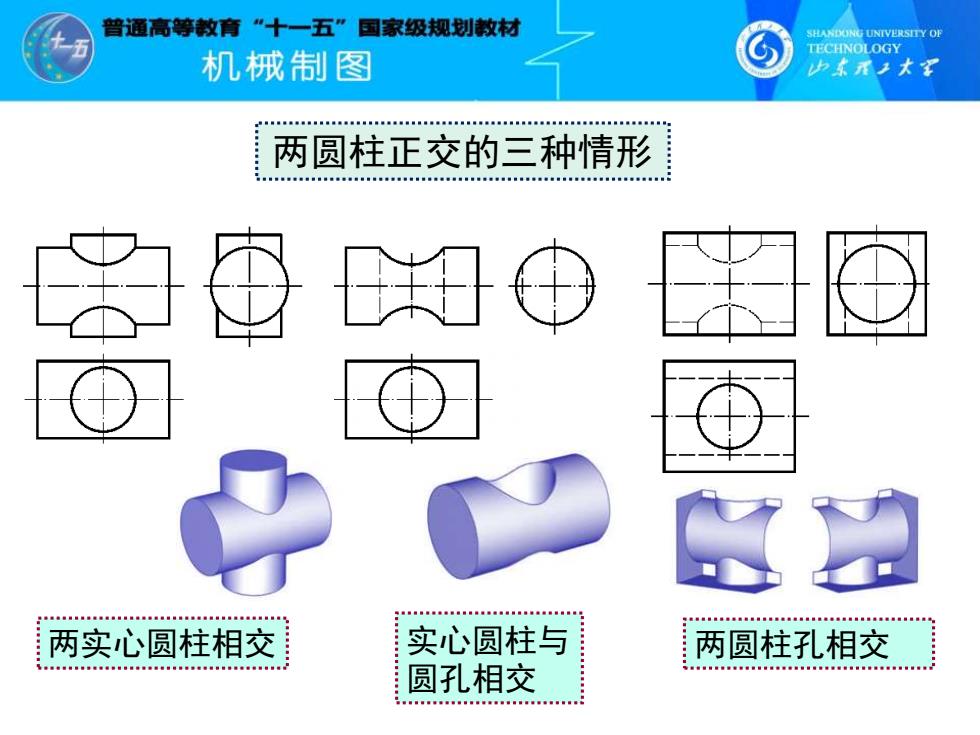
曾通高等教育”十一五”国家级规划敕材 SHANDONG UNIVERSITY OF TECHNOLOGY 机饿制图 少素承上木军 两圆柱正交的三种情形 , 两实心圆柱相交 实心圆柱与 两圆柱孔相交 ea。00。量。g。g0自0■。0 EEse知0■■e。g0e00。g 圆孔相交 5n0
两圆柱正交的三种情形 两实心圆柱相交 实心圆柱与 圆孔相交 两圆柱孔相交