
第十六章实验方法评价与数据处理 第一节实验方法评价 随着食品科学的不断发展,食品检验方法不断更新,评价检验方法的标准也逐步建立和 完善起来。这些评价标准主要是准确度、精密度、检测限以及费用与效益。 一.评价指标 1、准确府 准确度是指在一定条件下,多次测定的平均值与真实值相符合的程度。准确度通常用绝 对误差或相对误差表示。 在实际工作中,一般在试样中添加己知标准物质量作为真值,并以回收率表示准确度。 即: P%=X-Xx100% 16-1 m 式中:P(%) 一加入标准物质的回收率: X,一加标样品测定值 X 一试样本底测定值 —加入标准物质的质量 式中的本底值X0,其测定精密度所显示误差是反映随机误差:加入标准物质的质量m 其测定误差反映了系统误差。所以,回收率是两种误差综合指标,能决定方法的可靠性。 对回收率的要求数值是个比较复杂的问题,依分析测定方法难易和不同类型的分析方法而 变化。一般ppm级应在90%以上:Ppb级如荧光法测定苯并花在80%:比较繁杂的方法70% 即可:但最低不能小于70%。 2、精密度 精密度是指多次重复测定某一样品时,所得测定值的离散程度。精密度通常用标准差或 相对标准差来表示。 重复测定的精密度与待测物质绝对量有关,一般规定:mg级Cv(变异系数或相对标准 狗级C为10呢级为0左右 检测限是指分析方法在适当的置信水平内,能从样品检测被测组分的最小量或最小浓 度,即断定样品中被测组分的量或浓度确实高于空白中被测组分的最低量。 一般对检测限有几种规定方法: (1)气相色谱法:用最小检测量或最小检测浓度表示 最小检测量是指检测器恰能产生色谱峰高大于二倍噪音时的最小进样最。即: S-2N 163 式中:S最小响应值 N噪音信号 最小检测浓度是指最小检测量与进样量体积之比。即单位进样量相当待测物质的量。 例16-1用气相色谱法测定聚氯乙烯成型品中氯乙烯单体的检测限。仪器噪音的最大信 号为峰高1.0mm,注入0.5ug氯乙烯标准制备的顶空气3ml,响应值为12mm,求最低检测 题解:根据公式[16-21S=2N=2×1.0mm=2.0mm
第十六章 实验方法评价与数据处理 第一节 实验方法评价 随着食品科学的不断发展,食品检验方法不断更新,评价检验方法的标准也逐步建立和 完善起来。这些评价标准主要是准确度、精密度、检测限以及费用与效益。 一.评价指标 1、准确度 准确度是指在一定条件下,多次测定的平均值与真实值相符合的程度。准确度通常用绝 对误差或相对误差表示。 在实际工作中,一般在试样中添加已知标准物质量作为真值,并以回收率表示准确度。 即: 16-1 式中:P(%)——加入标准物质的回收率; X1——加标样品测定值 X0——试样本底测定值 m——加入标准物质的质量 式中的本底值 Xo,其测定精密度所显示误差是反映随机误差;加入标准物质的质量 m, 其测定误差反映了系统误差。所以,回收率是两种误差综合指标,能决定方法的可靠性。 对回收率的要 求数值是个比较复杂的问题,依分析测定方法难易和不同类型的分析方法而 变化。一般 ppm 级应在 90%以上;ppb 级如荧光法测定苯并芘在 80%;比较繁杂的方法 70% 即可;但最低不能小于 70%。 2、精密度 精密度是指多次重复测定某一样品时,所得测定值的离散程度。精密度通常用标准差或 相对标准差来表示。 重复测定的精密度与待测物质绝对量有关,一般规定:mg 级 Cv(变异系数或相对标准 差)为 5%;μg 级 Cv 为 10%,ng 级 Cv 为 50%左右。 3、检测限 检测限是指分析方法在适当的置信水平内,能从样品检测被测组分的最小量或最小浓 度,即断定样品中被测组分的量或浓度确实高于空白中被测组分的最低量。 一般对检测限有几种规定方法: (1)气相色谱法:用最小检测量或最小检测浓度表示 最小检测量是指检测器恰能产生色谱峰高大于二倍噪音时的最小进样量。即: S=2N 16-2 式中:S-最小响应值 N-噪音信号 最小检测浓度是指最小检测量与进样量体积之比。即单位进样量相当待测物质的量。 例 16-1 用气相色谱法测定聚氯乙烯成型品中氯乙烯单体的检测限。仪器噪音的最大信 号为峰高 1.0mm,注入 0.5ug 氯乙烯标准制备的顶空气 3ml,响应值为 12mm,求最低检测 量? 题解:根据公式[16-2] S=2N=2×1.0mm=2.0mm (%) 1 0 ×100% − = m X X P

最小检测量 注入标准物质量 可知道 最小响应值 标准物质的响应值 最小检测量=最小响应值×注入标准物质量-2X052=083e 标准物质的响应值 例16-2在上例中,如果注入3ml顶空气相当于0.5g聚氯乙烯成型品,求最小检测浓度? 题解:最小检测浓度-0.083/0.5=0.17ugg (2)吸光光度法 在吸光光度法中,扣除空白值后,吸光值为0.01所对应的浓度做为检测限。 例163利用镉离子与6溴苯并噻唑偶氨萘酚形成红色络合物,对食品中镉含量进行比 色测定。对全试剂空白进行5次平行测定,吸光度平均值是0.003,再测定0.25g标准镉溶 液,其吸光度为0.023,求检测限? 检测限 锅标准质量 题解:由最小响应值=镉标准吸光度一空白吸光度可以知道: 最小响应值×幅标准质量 检测限= 镉标准吸光度-空白吸光度=0.01×0.25/0.023-0.003=0.125ug (3)一般实验:当空白测定次数N>20时,给出置信水平95%,检测限为空白值正标 准差(S)的4.6倍。即:检测限=4.6× 16-3 例16-4在例16-3中,当空白测定N>20时,吸光度0.003士0.001相当于镉0.0375± 0.01 g求检测限? 题解:按式[16-3]检测限=4.6×S=4.6×0.013-0.06g 若空白测定次数n<20时,检测限按下式计算 检测限=2√21,S 16-4 式中:t置信水平为95%(单侧),批内自由度为f时的临界值 批内自由度 与m(n-l),m为重复测定次数, n为平行测定次数。 例16-5用2、3一二氨基萘荧光法测定硒,双空白测定10次,其空白值为11.4士1.3g, 求检测限? 题解:根据=m(n-1=10*2.1=10 查附表,当置信水平95%(单侧)时,10223 按式16-4小,检测限=221,S=2×1.414×223×1.3=8.20ng (4)国际理论应用化学联合会对检测限的规定 对于各种光学分析方法,可测量的最小分析响应值以下式表示 XL=。-K×S。 16-5 式中:X-最小响应值 。-多次测量空白值的平均值(n≥20) S。-多次测量空白值的标准差:
由 = 可知道 =2×0.5/12=0.083ug 例 16-2 在上例中,如果注入 3ml 顶空气相当于 0.5g 聚氯乙烯成型品,求最小检测浓度? 题解:最小检测浓度=0.083/0.5=0.17μg/g (2)吸光光度法 在吸光光度法中,扣除空白值后,吸光值为 0.01 所对应的浓度做为检测限。 例 16-3 利用镉离子与 6-溴苯并噻唑偶氮萘酚形成红色络合物,对食品中镉含量进行比 色测定。对全试剂空白进行 5 次平行测定,吸光度平均值是 0.003,再测定 0.25μg 标准镉溶 液,其吸光度为 0.023,求检测限? 题解: 由 最小响应值 检测限 = 镉标准吸光度 空白吸光度 镉标准质量 − 可以知道: 镉标准吸光度 空白吸光度 最小响应值 镉标准质量 检测限 − × = =0.01×0.25/0.023-0.003=0.125ug (3)一般实验:当空白测定次数 N>20 时,给出置信水平 95%,检测限为空白值正标 准差(S)的 4.6 倍。即:检测限=4.6×S 16-3 例 16-4 在例 16-3 中,当空白测定 N>20 时,吸光度 0.003±0.001 相当于镉 0.0375± 0.013μg 求检测限? 题解:按式[16-3]检测限=4.6×S=4.6×0.013=0.06μg 若空白测定次数 n<20 时,检测限按下式计算 t Sf 检测限 = 2 2 16-4 式中;tf-置信水平为 95%(单侧),批内自由度为 f 时的临界值 f-批内自由度 f=m(n-1),m 为重复测定次数, n 为平行测定次数。 例 16-5 用 2、3 一二氨基萘荧光法测定硒,双空白测定 10 次,其空白值为 11.4±1.3ng, 求检测限? 题解:根据 f=m(n-1)=10*(2-1)=10 查附表,当置信水平 95%(单侧)时,t10=2.23 按式[16-4], =2×1.414×2.23×1.3=8.20ng (4)国际理论应用化学联合会对检测限的规定 对于各种光学分析方法,可测量的最小分析响应值以下式表示 X L = Xb − K × Sb 16-5 式中:XL-最小响应值; Xb − 多次测量空白值的平均值(n≥20); Sb- 多次测量空白值的标准差; 检测限 = 2 2t f S 最小响应值 最小检测量 标准物质的响应值 注入标准物质量 标准物质的响应值 最小响应值 注入标准物质量 最小检测量 × =

K-根据一定置信水平确定的系数(一般当置信水平为90%,空白测量次数<20时,K=3: 置信水平为95%,n>20时,K=4.65). 规定,检测限=七足。K×S 16-.6 式中,m为方法灵敏度,即单位浓度或单位量被则物质所产生的响应值的变化程度,在实际 工作中,以标准曲线斜率度量灵敏度,基余各项符号同式[165]。 例166在例16.5测定西时,物加空白则定数,比空白俏为:101+095ng,其灵敏府 为0.54荧光单位e,求检测限 题解:按16-6 检测限=-无-K×S =3×0.95/0.54=528ng m 从检测限定义可以知道,增加实际测定次数,提高测定精密度,降低仪器噪音,可以改 善检测限。 4、费用与效益 费用与效益是目前国内外重视的问题。实验室工作人员,应结合实际测试目标,选择或 设计相应准确度和精密度的实验方法。用一般常规实验能够完成的测定,不必使用贵重精密 仪器。检验员经训练能较好堂据某种测定方法的时间,也是评价实验方法的重要内容。“简 单易学”在一定程度上意味着能保证检验质量。从实际工作需要出发,快速,微量,费用低 技术要求不高,操作安全的测定方法应列为一般实验室的首选方法 ,实验结果的检验 在食品分析中,常遇到两个平均值的比较问题,如测定平均值和己知值的比较,不同分 析人员,不同实验室,或用不同分析方法测定的平均值的比较,对比性试验研究等均属于此 类问题。所以对这类问题常采用显著性检验法利用统计方法来检验被处理问题是否存 在统计上的显若性,常用有1检验法和F检验法 1、t检验法 用以比较一个平均值与标准值之间或两个平均值之间是否有在显著性差异。 进行t检验的程序如下: (1)选定所用的检验统计量: 当检验样本均值下与总体均值μ是否有显著性差异时,使用统计量 灭-4 16-7 式中:、一标准差 当检验两个均值之间是否有显著性差异时,使用统计量 n1×n2 Vm+nz 16-8 其中S合并标准差 按下式计算: 5= -1)S+(n2-10S n1+n2-2 16-9
K-根据一定置信水平确定的系数(一般当置信水平为 90%,空白测量次数 n<20 时,K=3; 置信水平为 95%,n>20 时,K=4.65)。 规定: m K S m X L Xb × b = − 检测限 = 16-6 式中,m 为方法灵敏度,即单位浓度或单位量被则物质所产生的响应值的变化程度,在实际 工作中,以标准曲线斜率度量灵敏度,基余各项符号同式[16-5]。 例 16-6 在例 16-5 测定硒时,增加空白测定数,其空白值为:10.1±0.95ng,其灵敏度 为 0.54 荧光单位/ng,求检测限? 题解:按 16-6 式 =3×0.95/0.54=5.28ng 从检测限定义可以知道,增加实际测定次数,提高测定精密度,降低仪器噪音,可以改 善检测限。 4、费用与效益 费用与效益是目前国内外重视的问题。实验室工作人员,应结合实际测试目标,选择或 设计相应准确度和精密度的实验方法。用一般常规实验能够完成的测定,不必使用贵重精密 仪器。检验员经训练能较好掌握某种测定方法的时间,也是评价实验方法的重要内容。“简 单易学”在一定程度上意味着能保证检验质量。从实际工作需要出发,快速,微量,费用低 廉,技术要求不高,操作安全的测定方法应列为一般实验室的首选方法。 二.实验结果的检验 在食品分析中,常遇到两个平均值的比较问题,如测定平均值和已知值的比较,不同分 析人员,不同实验室,或用不同分析方法测定的平均值的比较,对比性试验研究等均属于此 类问题。所以对这类问题常采用显著性检验法-利用统计方法来检验被处理问题是否存 在统计上的显著性,常用有 t 检验法和 F 检验法。 1、t 检验法 用以比较一个平均值与标准值之间或两个平均值之间是否有在显著性差异。 进行 t 检验的程序如下: (1)选定所用的检验统计量: 当检验样本均值 X 与总体均值 μ 是否有显著性差异时,使用统计量 S n X t / − μ = 16—7 式中:S—标准差 当检验两个均值之间是否有显著性差异时,使用统计量 1 2 1 2 1 2 n n n n S X X t + × × − = 16—8 其中 S -合并标准差 按下式计算: 2 ( 1) ( 1) 1 2 2 2 2 2 1 1 + − − + − = n n n S n S S 16—9 m K S m XL Xb × b = − 检测限 =

式中S第一个样本的方差 S第二个样本的方差 n4一第一个样本的测定次数 2一第二个样本的测定次数 (2)计算统计量, 如果由样本值计算的统计量值大于t分布表中相应显著性水平α和相应自由度f下的临 界值。则表明被检验的均值有显若性差异,反之,差异不显若。 应用↑检验时,垫求被检险的两组数据具有相同或相近的方差(标准差)。因此在↑检 验之前必须进行F检验,只有在两方差一致性前提下才能进行t检验。 (3)假设检验的一尾测验与两尾测验 在进行测验结果分析确定检验水平时,还应根据其处理的性质和试验结果的准确性,考 虑显著性测验用 尼测验还是用两尾测 在提出一个统计假设时,必然有一个与其相对应的备择假设。备择假设为否定假设时, 必然接受的另一个假设。例如,单个平均数进行显著性测验时,通常H0:u一o,H:μ≠o。 如果H被否定接受H时,其μ≠,便有μ大于或小于的两种可能性,即所测定的 误差概率在正态分布曲线的左尾和右尾各有一个否定域,而附表中临界值表规定的。 值是两尾概率之 ,如果确定的检验水平a-0.05,则两尾否定域的概率各为0.025,这类测 验称这为两尾测验 但有的试验则不然,例如某酿酒厂曲种酿造醋的醋酸含量大于12%,则其假设H:“ >12%,H:μ≤12%。如果选择的曲种粮造醋酸含量大于12%,H6被否定,μ只能大于12%。 若小于12%。便不符合规定的企业标准,没有推广价值,因此只有在正态曲线的右尾一个否 定域,这类检验称为一尾测验。两尾测验查两尾概表或一尾测验查 尾概率表时,可以直接 从表上查得。如果两尾检验查一尾概表时,需将检验水平值除 再查出。值,如两尾测 验检验水平a=0.05,一尾概率00s=1.64,应将检验水平=0.05除以2得=0.025,0ms=224, 如果一尾检验查两尾概率表时需将检验水平值乘以2,再查出值,如一尾检验水平a=0.1, o=1.64,因此用一尾测验还是用两尾测验,应认真从实际考虑。 而1检验法为判别性测验,多为两尾测验。 下面将t检验法在食品分析中的主要应用介绍如下 ①用已知组成的标样评价分析方法 为了鉴定一个分析方法的可靠性,可用一已知量的基准物或已知含量的标准试样进行对 照试验,通过若干次测定,取得其平均值,然后将这个平均值与已知值(真值)进行比较, 从而制断这个分析方法是否存在系统误差。因为这时将平均值与真值进行比较,所以可以按 t检验法来判别。 逻辑推理是先假设平均值与真值之间不存在真正的差异, 如果所算出的 值大于通常规定的置信水平的t值,那么,应该拒绝所提的假设,就是说,这样的差异不 认为是偶然的误差,而是被检验的方法存在系统误差,反之,则应接该受假设,判断该方法 不存在系统误差, 例16-7为了鉴定一个分析方法的准确度,取重量为100mg的基准物进行10次测定, 所得数据为100.3,992,99.4,100.0,99.7,99.9,99.4,100.1,99.4,99.6,试对这组数据 进行评价。 题解:计算平均值和标准偏差。X=99.7,S=0.38,按式16-7,计算统计量
式中 2 S1 -第一个样本的方差 2 S2 -第二个样本的方差 n1-第一个样本的测定次数 n2-第二个样本的测定次数 (2)计算统计量, 如果由样本值计算的统计量值大于 t 分布表中相应显著性水平 α 和相应自由度 f 下的临 界值 tα, f,则表明 被检验的均值有显著性差异,反之,差异不显著。 应用 t 检验时,要求被检验的两组数据具有相同或相近的方差(标准差)。因此在 t 检 验之前必须进行 F 检验,只有在两方差一致性前提下才能进行 t 检验。 (3)假设检验的一尾测验与两尾测验 在进行测验结果分析确定检验水平时,还应根据其处理的性质和试验结果的准确性,考 虑显著性测验用一尾测验还是用两尾测验。 在提出一个统计假设时,必然有一个与其相对应的备择假设。备择假设为否定假设时, 必然接受的另一个假设。例如,单个平均数进行显著性测验时,通常 H0:μ=μ0,HA:μ≠μ0。 如果 H0 被否定接受 HA时,其 μ≠μ0,便有 μ 大于 μ0或小于 μ0的两种可能性,即所测定的 误差概率在正态分布曲线的左尾和右尾各有一个否定域,而附表_1_中临界 t 值表规定的 α 值是两尾概率之和。如果确定的检验水平 α=0.05,则两尾否定域的概率各为 0.025,这类测 验称这为两尾测验。 但有的试验则不然,例如某酿酒厂曲种酿造醋的醋酸含量大于 12%,则其假设 H0:μ >12%,HA:μ≤12%。如果选择的曲种酿造醋酸含量大于 12%,H0 被否定,μ 只能大于 12%。 若小于 12%便不符合规定的企业标准,没有推广价值,因此只有在正态曲线的右尾一个否 定域,这类检验称为一尾测验。两尾测验查两尾概表或一尾测验查一尾概率表时,可以直接 从表上查得。如果两尾检验查一尾概表时,需将检验水平值除 2,再查出 µα 值,如两尾测 验检验水平 α=0.05,一尾概率 µ0.05=1.64,应将检验水平 α=0.05 除以 2 得 α=0.025,µ0.025=2.24, 如果一尾检验查两尾概率表时需将检验水平值乘以 2,再查出 µα值,如一尾检验水平 α=0.1, µ0.1=1.64,因此用一尾测验还是用两尾测验,应认真从实际考虑。 而 t 检验法为判别性测验,多为两尾测验。 下面将 t 检验法在食品分析中的主要应用介绍如下: ①用已知组成的标样评价分析方法 为了鉴定一个分析方法的可靠性,可用一已知量的基准物或已知含量的标准试样进行对 照试验,通过若干次测定,取得其平均值,然后将这个平均值与已知值(真值)进行比较, 从而制断这个分析方法是否存在系统误差。因为这时将平均值与真值进行比较,所以可以按 t 检验法来判别。逻辑推理是先假设平均值与真值之间不存在真正的差异,如果所算出的 t 值大于通常规定的置信水平的 t 值,那么,应该拒绝所提的假设,就是说,这样的差异不能 认为是偶然的误差,而是被检验的方法存在系统误差,反之,则应接该受假设,判断该方法 不存在系统误差。 例 16-7 为了鉴定一个分析方法的准确度,取重量为 100mg 的基准物进行 10 次测定, 所得数据为 100.3,99.2,99.4,100.0,99.7,99.9,99.4,100.1,99.4,99.6,试对这组数据 进行评价。 题解:计算平均值和标准偏差。 X =99.7,S=0.38,按式 16—7,计算统计量
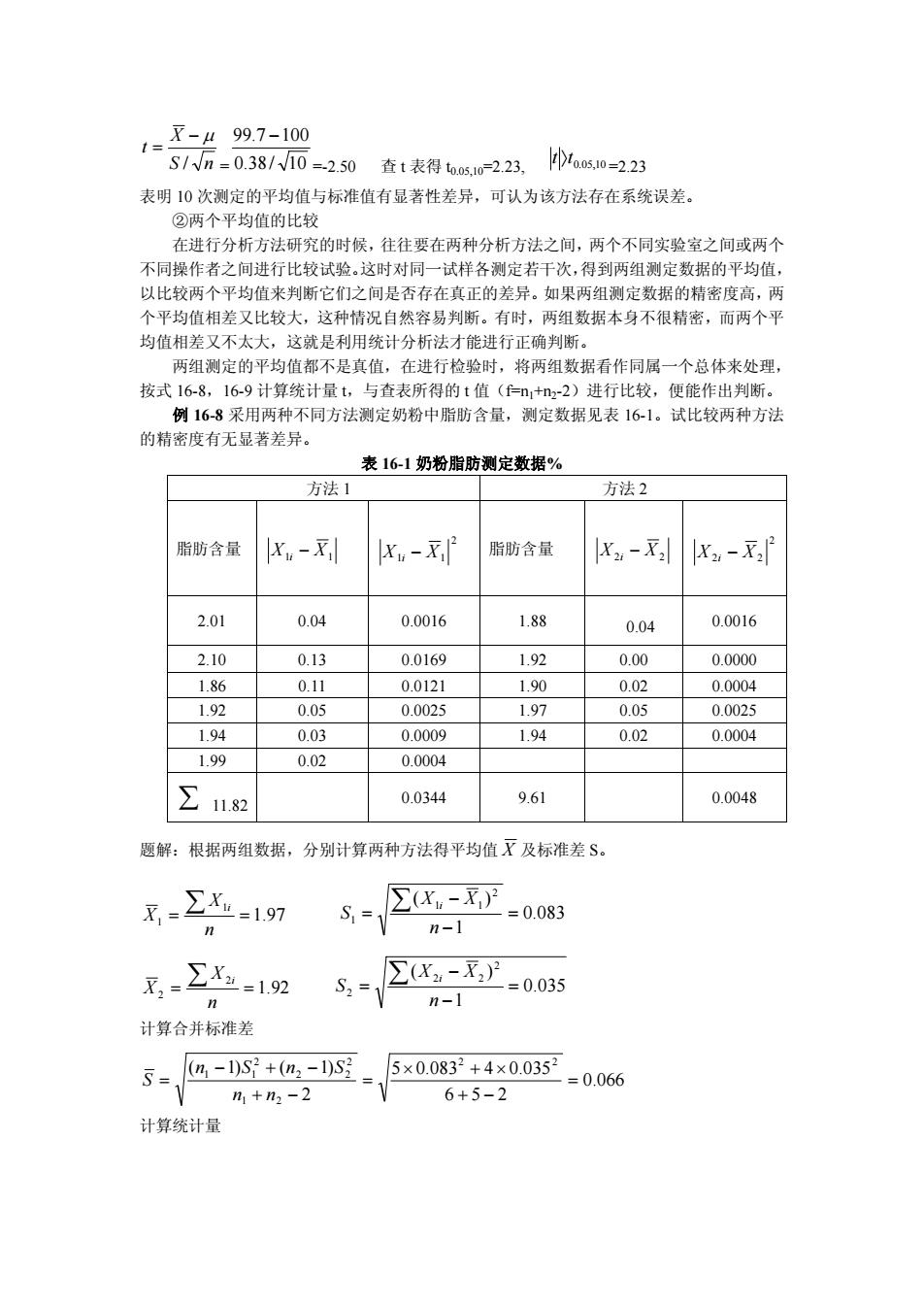
1=X-497-10 S1.0.38/而=-250查1表得6w223.ps0=223 表明10次测定的平均值与标准值有显著性差异,可认为该方法存在系统误差 ②两个平均值的比较 在进行分析方法研究的时候,往往要在两种分析方法之间,两个不同实验室之间或两个 不同操作者之间进行比较试验。这时对同一试样各测定若干次,得到两组测定数据的平均值, 以出较两个平均值来判断它们之间是否存在直正的差异。加里两组删定数据的持密度高。两 个平均值相差又比较大, 这种情况自然容易判断。有时,两组数据本身不很精密,而两个平 均值相差又不太大,这就是利用统计分析法才能进行正确判断。 两组测定的平均值都不是真值,在进行检验时,将两组数据看作同属一个总体来处理, 按式16-8,16-9计算统计量t,与查表所得的t值(f=n+m2-2)进行比较,便能作出判断。 例16-8采用两种不同方法测定奶粉中脂肪含量,测定数据见表16-1。试比较两种方法 的精密度有无显著差异。 表161奶粉脂肪测定数据% 方法1 方法2 脂肪含量 Xv-X x-Xl 脂肪含量 X-X2x2-X2 2.01 0.04 0.0016 1.88 0.04 0.0016 210 0.13 0.0169 1.92 000 00000 1.86 0.11 0.0121 1.90 0.02 0.0004 1.92 0.05 0.0025 1.97 0.05 0.0025 194 003 00009 1.94 0.02 0.0004 1g0 0.02 0.0004 ∑182 0.0344 9.61 0.0048 题解:根据两组数据,分别计算两种方法得平均值灭及标准差$。 X=∑X=197 S,= ∑(Xw-x)7 =0.083 n-1 ,=X-192 ∑(X-x2) =0.035 n- 计算合并标准差 5=4-0s+a,-sg 5×0.0832+4×0.0352 =0.066 m+n2-2 6+5-2 计算统计量
S n X t / − μ = = 0.38/ 10 99.7 −100 =-2.50 查 t 表得 t0.05,10=2.23, 0.05,10 t 〉t =2.23 表明 10 次测定的平均值与标准值有显著性差异,可认为该方法存在系统误差。 ②两个平均值的比较 在进行分析方法研究的时候,往往要在两种分析方法之间,两个不同实验室之间或两个 不同操作者之间进行比较试验。这时对同一试样各测定若干次,得到两组测定数据的平均值, 以比较两个平均值来判断它们之间是否存在真正的差异。如果两组测定数据的精密度高,两 个平均值相差又比较大,这种情况自然容易判断。有时,两组数据本身不很精密,而两个平 均值相差又不太大,这就是利用统计分析法才能进行正确判断。 两组测定的平均值都不是真值,在进行检验时,将两组数据看作同属一个总体来处理, 按式 16-8,16-9 计算统计量 t,与查表所得的 t 值(f=n1+n2-2)进行比较,便能作出判断。 例 16-8 采用两种不同方法测定奶粉中脂肪含量,测定数据见表 16-1。试比较两种方法 的精密度有无显著差异。 表 16-1 奶粉脂肪测定数据% 方法 1 方法 2 脂肪含量 X1i − X1 2 X1i − X1 脂肪含量 X 2i − X 2 2 X 2i − X 2 2.01 0.04 0.0016 1.88 0.04 0.0016 2.10 0.13 0.0169 1.92 0.00 0.0000 1.86 0.11 0.0121 1.90 0.02 0.0004 1.92 0.05 0.0025 1.97 0.05 0.0025 1.94 0.03 0.0009 1.94 0.02 0.0004 1.99 0.02 0.0004 ∑ 11.82 0.0344 9.61 0.0048 题解:根据两组数据,分别计算两种方法得平均值 X 及标准差 S。 1.97 1 1 = = ∑ n X X i 0.083 1 ( ) 2 1 1 1 = − − = ∑ n X X S i 1.92 2 2 = = ∑ n X X i 0.035 1 ( ) 2 2 2 2 = − − = ∑ n X X S i 计算合并标准差 0.066 6 5 2 5 0.083 4 0.035 2 ( 1) ( 1) 2 2 1 2 2 2 2 2 1 1 = + − × + × = + − − + − = n n n S n S S 计算统计量