
第5章分析力学 对于完整约束体系设3个广义坐标分别为q1,.,9则个质点组成的 力学体系全体3n个坐标,均可用下式表示 x;=x,(q1,q2,.,qs,t) i=1,2,.,3n 上式称为变换方程 5.2虚功原理 (1)实位移与虚位移 1、实位移:质点按照运动定律真实发生的位移。表示成厅
第5章 分析力学 对于完整约束体系设 个广义坐标分别为 则 个质点组成的 力学体系全体 个坐标,均可用下式 表示 s q qs , , 1 n 3n ( , , , , ) 1 2 x x q q q t i = i s i = 1,2, ,3n 上式称为变换方程 5.2 虚功原理 (1)实位移与虚位移 1、实位移:质点按照运动定律真实发生的位移。表示成 dr

第5章分析力学 2、虚位移:在当前约束许可的情形下虚拟发生的位移。表示成 3、虚功:W=F.币 4、理想约束 设体系所受到的约束力为,.R,,满足以下关系则构成理想约束 2反成=0 i=
第5章 分析力学 2、虚位移:在当前约束许可的情形下虚拟发生的位移。表示成 r 3、虚功: W F δr = 4、理想约束 设体系所受到的约束力为 R , Rn ,满足以下关系则构成理想约束 1 0 1 = = n i i i R δr

第5章分析力学 光滑曲面,刚性连杆,不可伸长轻绳等都可视为理想约束 5、虚功原理 理想约束下的力学体系,当处于平衡状态时,全体主动力的虚功 之和为零。即 E·访=0 虚功原理在表达力学平衡体系时是完备的,这表现在它与牛顿定 律的等价性
第5章 分析力学 光滑曲面,刚性连杆,不可伸长轻绳等都可视为理想约束 理想约束下的力学体系,当处于平衡状态时,全体主动力的虚功 之和为零。即 5、虚功原理 0 1 = = n i i i F δr 虚功原理在表达力学平衡体系时是完备的,这表现在它与牛顿定 律的等价性

第5章分析力学 按照牛顿定律,平衡体系应满足 豆R=0 取上式的虚功,有 立6+)成=0 即 立疗所=0 上式称为虚功原理
第5章 分析力学 按照牛顿定律,平衡体系应满足 ( ) 0 1 + = = n i Fi Ri 取上式的虚功,有 ( ) 0 1 + = = n i i i i F R r 即 0 1 = = n i i i F δr 上式称为虚功原理
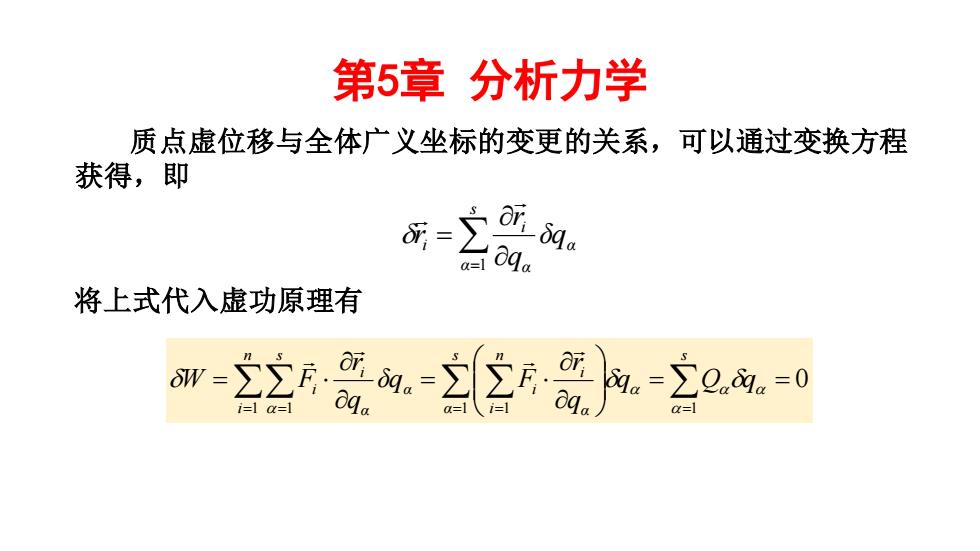
第5章分析力学 质点虚位移与全体广义坐标的变更的关系,可以通过变换方程 获得,即 将上式代入虚功原理有 m-22-空恶-0-0
第5章 分析力学 质点虚位移与全体广义坐标的变更的关系,可以通过变换方程 获得,即 = = s α α α i i δq q r r 1 将上式代入虚功原理有 = = = = = = = = = n s i s s α n i α i α i α i i q Q q q r δq F q r W F 1 1 1 1 1 0