
第五节 简谐波 习题5-8试利用能流密度的 概念求球面波的表达式。 解介质无吸收,单位时间 通过两个球面的能流相等: IS =12S2 即 ptou-2p5ou月 1 2 A1=乃 y=4 cosou-) A 中Y为离开波源的距离,A,为r=1处的振幅
习题5-8 试利用能流密度的 概念求球面波的表达式。 解 介质无吸收,单位时间 通过两个球面的能流相等: 1 s 2 s 1 r 2 r 1 2 2 1 r r A A = 0 cos ( ) A r y t r u = − 1 1 2 S2 I S = I 2 2 2 2 2 2 1 2 2 1 4π 2 1 4π 2 1 即 A u r = A u r 第五节 简谐波 式中 r 为离开波源的距离, 为 r =1 处的振幅. A0
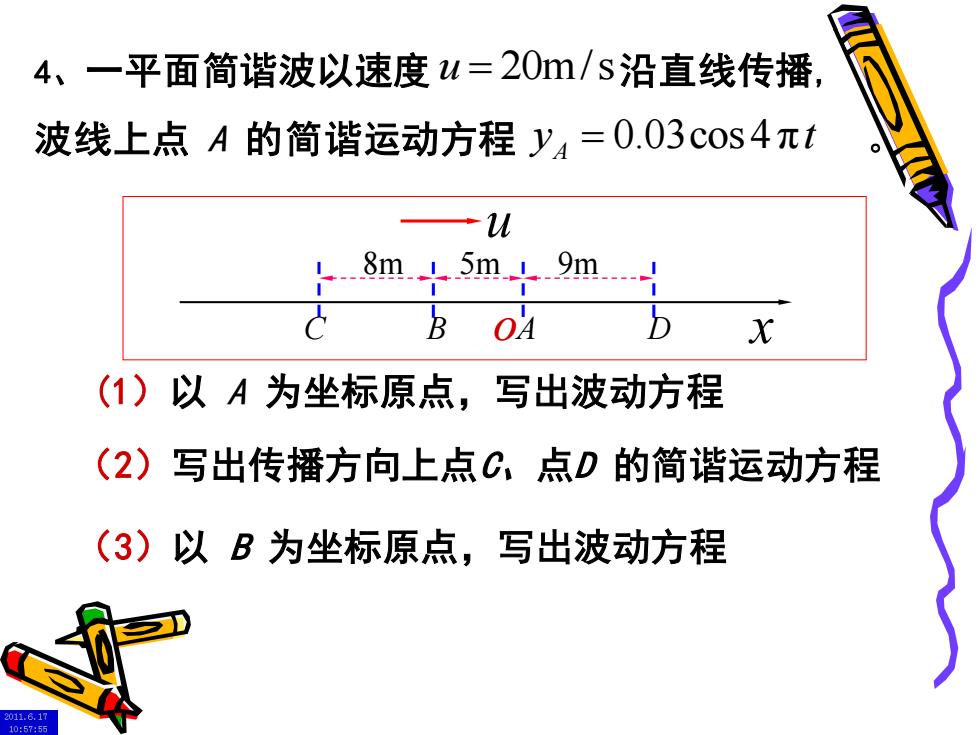
4、一平面简谐波以速度u=20m/s沿直线传播, 波线上点A的简谐运动方程y4=0.03c0s4πt ↓8m.↓5m.4.9m X (1)以A为坐标原点,写出波动方程 (2)写出传播方向上点C,点D的简谐运动方程 (3)以B为坐标原点,写出波动方程
4、一平面简谐波以速度 沿直线传播, 波线上点 A 的简谐运动方程 。 u = 20m/s 0.03cos 4π A y t = (1)以 A 为坐标原点,写出波动方程 u C B A D 5m 9m o x 8m (3)以 B 为坐标原点,写出波动方程 (2)写出传播方向上点C、点D 的简谐运动方程