
❖ 由于约束方程有两个求知数,所以可用图解 法解之。下面运用图解法解出使目标函数 Z=253X+528Y为最大的X、Y值。 ❖ 建立直角坐标系,如图1-1。将方程1取等号 有: ❖ 547X+1872Y=200000 ❖ 令X=0,得Y=106.8,得到点D(0,106.8) ❖ 令Y=0,得X=365.6,得到点D65.6,0) 第一章 养猪生产的筹划
❖ 由于约束方程有两个求知数,所以可用图解 法解之。下面运用图解法解出使目标函数 Z=253X+528Y为最大的X、Y值。 ❖ 建立直角坐标系,如图1-1。将方程1取等号 有: ❖ 547X+1872Y=200000 ❖ 令X=0,得Y=106.8,得到点D(0,106.8) ❖ 令Y=0,得X=365.6,得到点D65.6,0) 第一章 养猪生产的筹划
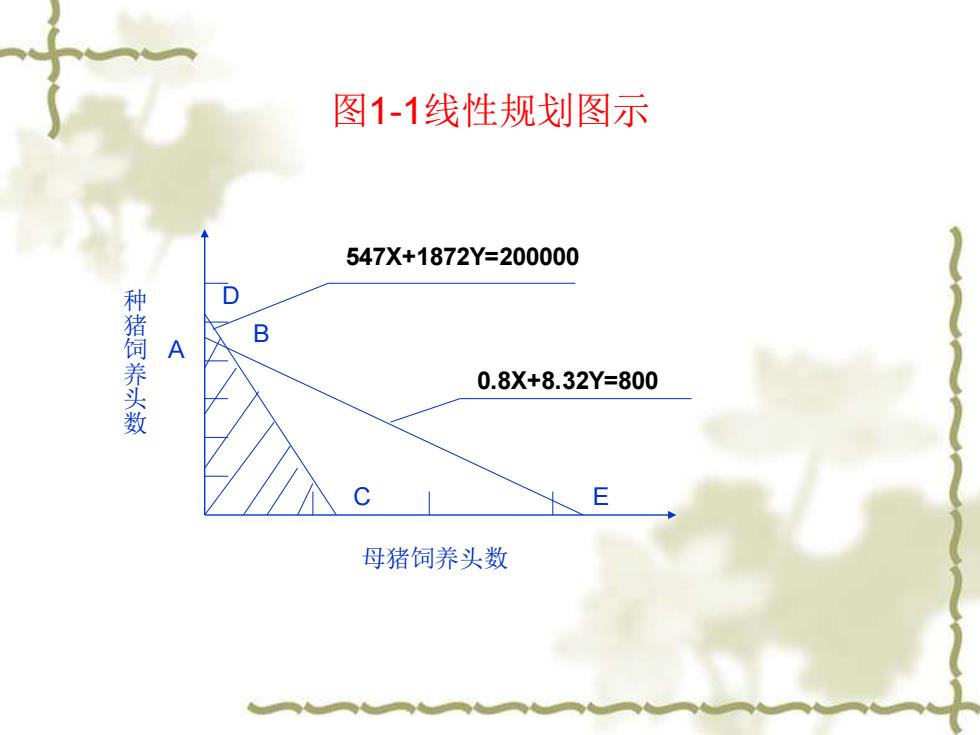
图1-1线性规划图示 547X+1872Y=200000 0.8X+8.32Y=800 C E B D A 母猪饲养头数 种 猪 饲 养 头 数
图1-1线性规划图示 547X+1872Y=200000 0.8X+8.32Y=800 C E B D A 母猪饲养头数 种 猪 饲 养 头 数

❖ 由方程3 ,4得知,则值都在每一象限 。 ❖ 由如图1-1可看出: ❖ 在ABD范围内,有资金而无猪舍; ❖ 在BCE 范围内,有猪舍而无资金; ❖ 在DBE三点以外的范围中,既无资金又无猪 舍。 ❖ 以上三种情况都不能使生产进行。只有在四 边形OABC区域内取值,生产才是可行的。 第一章 养猪生产的筹划
❖ 由方程3 ,4得知,则值都在每一象限 。 ❖ 由如图1-1可看出: ❖ 在ABD范围内,有资金而无猪舍; ❖ 在BCE 范围内,有猪舍而无资金; ❖ 在DBE三点以外的范围中,既无资金又无猪 舍。 ❖ 以上三种情况都不能使生产进行。只有在四 边形OABC区域内取值,生产才是可行的。 第一章 养猪生产的筹划

❖ 以上三种情况都不能使生产进行。只有在 四边形OABC区域内取值。生产才是可行的。 但要使目标函数值最大,只有取四边形上 凸点的值。从图1-1上可知,可行解区域四 边形OABC上的凸点O、A、B、C是四点。 其中,O是原点,为未生产状态,Z值为0; A、B、C三点是生产状态。求出三个点的 值,分别代入目标函数方程 Z=2×53×0+96×528中,比较其大小: ❖ 可知B 点(54,91) Z值使目标函数Z值最大. 即肉猪每批养殖54头,一年共108头(二批). 种母猪养91头,该场收益最大.按公母比例 1:25计,则 3头公猪。 第一章 养猪生产的筹划
❖ 以上三种情况都不能使生产进行。只有在 四边形OABC区域内取值。生产才是可行的。 但要使目标函数值最大,只有取四边形上 凸点的值。从图1-1上可知,可行解区域四 边形OABC上的凸点O、A、B、C是四点。 其中,O是原点,为未生产状态,Z值为0; A、B、C三点是生产状态。求出三个点的 值,分别代入目标函数方程 Z=2×53×0+96×528中,比较其大小: ❖ 可知B 点(54,91) Z值使目标函数Z值最大. 即肉猪每批养殖54头,一年共108头(二批). 种母猪养91头,该场收益最大.按公母比例 1:25计,则 3头公猪。 第一章 养猪生产的筹划

三、盈亏平衡分析法 也叫保本分析法,是分析在一定 时期内的产量、成本、利润之间 的相互关系,并通过计算盈亏临 界点或保本点产销量来测算在短 时期内某一生产项目是否为最佳 规模的方法。 第一章 养猪生产的筹划
三、盈亏平衡分析法 也叫保本分析法,是分析在一定 时期内的产量、成本、利润之间 的相互关系,并通过计算盈亏临 界点或保本点产销量来测算在短 时期内某一生产项目是否为最佳 规模的方法。 第一章 养猪生产的筹划