
3-1-3-3离散点数据的求积一 应用示例 合心 例1:实际气体逸度的计算 纯气体的逸度由定义: du=RTdInf=Vmadp (1) RT a='m理- m,实二 -V m,实 p RT ∴.V ,实= -a p 代入(1) RT RTdInf-(RI-@)dp p 积分,并取极低压力下气体视为理想气体,得 (2) 逸度:f=功·p 中为逸度系数 已知p~Vm数据
纯气体的逸度由定义: dμ = RTd ln f =Vm,实dp α α ∴ = − = = − p RT V V p RT V V m, 实 m, 理 - m, 实 m, 实 (1) 代入(1) p p RT RTd ln f = ( −α)d 积分,并取极低压力下气体视为理想气体,得 ∫ ∫ = = − = − p p p RT p p RT f 0 0 d d 1 ln ln α φ α 逸度:f = φ ⋅ p φ为逸度系数 (2) 例1: 实际气体逸度的计算 实际气体逸度的计算 已知p~Vm数据 3-1-3 –3 离散点数据的求积——应用示例
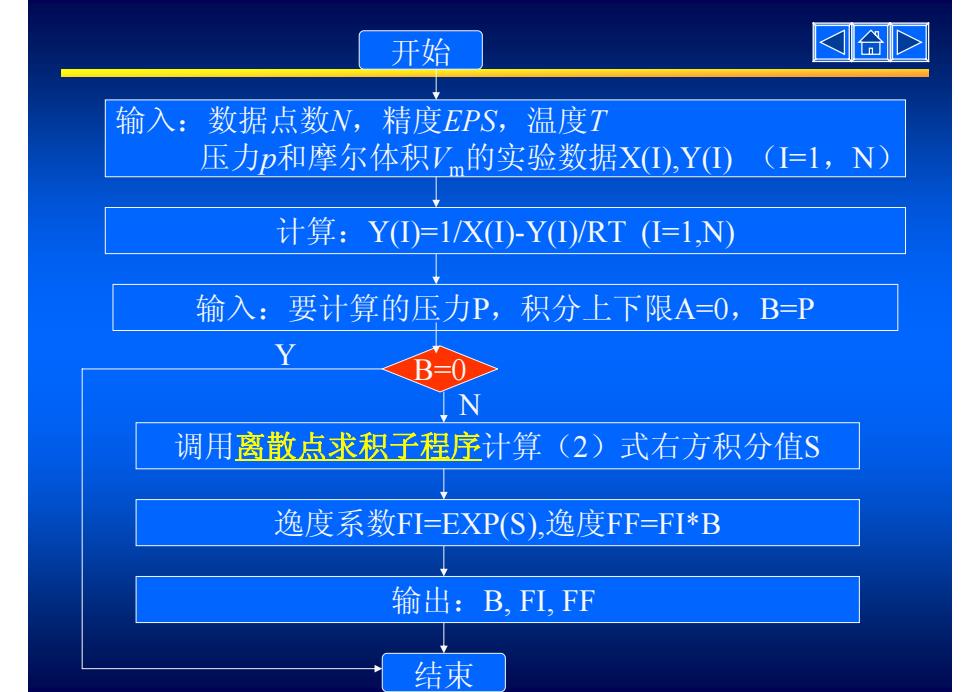
开始 I合) 输入: 数据点数N,精度EPS,温度T 压力p和摩尔体积Vm的实验数据X),Y①)(=1,N) 计算:YI)=1/X①)-YI)/RT(I=1,N 输入:要计算的压力P,积分上下限A=O0,B=P B=0 N 调用离散点求积子程序计算(2)式右方积分值S 逸度系数FI=EXP(S),逸度FF=FI*B 输出:B,FL,FF 结東
开始 输入:数据点数N,精度EPS,温度T 压力p和摩尔体积Vm的实验数据X(I),Y(I) (I=1,N) 输出:B, FI, FF 结束 调用离散点求积子程序计算(2)式右方积分值S 计算:Y(I)=1/X(I)-Y(I)/RT (I=1,N) 输入:要计算的压力P,积分上下限A=0,B=P B=0 Y N 逸度系数FI=EXP(S),逸度FF=FI*B

3-1-3-3离散点数据的求积一 应用示例 合心 例2:已知固体Pb的热容C,温度T数据,求从15K到550K 的固体Pb的焓变。 N-C,dT 例3:分子标准熵S及C。~T数据,求500K时的熵S值。 S,=S,+(C,/T7 T1:298.15KT:500K
例2:已知固体Pb的热容Cp~温度T数据,求从15K到550K 的固体Pb的焓变。 H C T T T p d 21 ∫ Δ = 例3:分子标准熵S及Cp~T数据,求500K时的熵S值。 S S C T T T T p ( / )d 21 2 1 ∫ = + T1:298.15K T2:500K 3-1-3 –3 离散点数据的求积——应用示例
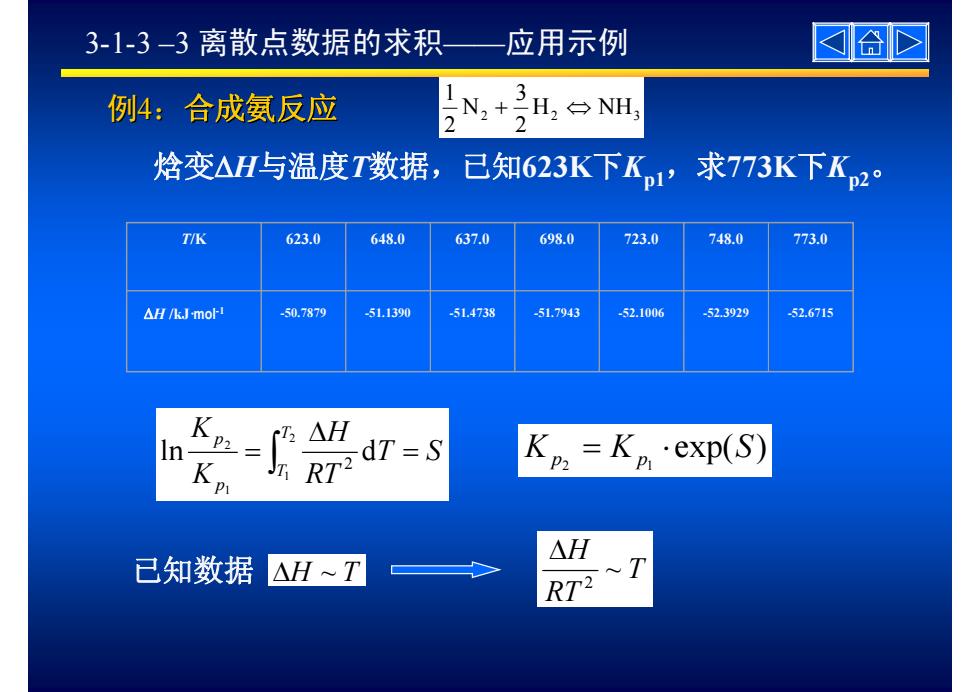
3-1-3-3离散点数据的求积— 应用示例 国合 例4:合成氨反应 N,+3H,台NE 焓变△H与温度T数据, 已知623K下K1 求773K下K2% TIK 623.0 648.0 637.0 698.0 723.0 748.0 773.0 △H/kJmo 50.7879 -51.1390 5L.4738 -51.7943 52.1006 52.3929 52.6715 2 rI△H dT=S Kp RT2 Kp,=Kn·exp(S) △H 已知数据△HT ~T RT2
exp( ) 2 1 K K S p p T S = ⋅ RTH KK TT pp = Δ = ∫ 21 12 ln d2 已知数据 T RTH ~ 2 Δ ΔH ~ T 例4:合成氨反应 2 H2 NH3 23 N21 + ⇔ 焓变ΔH与温度T数据,已知623K下Kp1,求773K下Kp2。 T/K 623.0 648.0 637.0 698.0 723.0 748.0 773.0 ΔH /kJ·mol-1 -50.7879 -51.1390 -51.4738 -51.7943 -52.1006 -52.3929 -52.6715 3-1-3 –3 离散点数据的求积——应用示例

3-1-3-3离散点数据的求积一 应用示例 合心 开始 输入:焓变与温度的实验数据X①,Y① (I=1,N) 计算:XI=X,Y(I)=Y①/XI*XI=1,N 输入:积分上、下限T2,T1及KP1 调用离散点求积子程序计算积分值$ 计算KP2=KP1*EXP(S/R) 输出:KP2 显示程序 结束 显示输出
开始 输入:焓变与温度的实验数据X(I),Y(I) (I=1,N) 输出:KP2 结束 调用离散点求积子程序计算积分值S 计算:XI=X(I),Y(I)=Y(I)/(XI*XI) (I=1,N) 输入:积分上、下限T2,T1及KP1 计算KP2=KP1*EXP(S/R) 显示程序 显示输出 3-1-3 –3 离散点数据的求积——应用示例