
3-2-1-2 Simpson法-方法原理 国合 判据 当S2n≤1时,S2n-Sn<EPS 当S2n>1时,(S2n-Sn)/S2n<EPS
判据: S S S S EPS S S S EPS n n n n n n n > − < ≤ − < 2 2 2 2 2 1 , ( )/ 1 , 当 时 当 时 3-2-1-2 Simpson法——方法原理
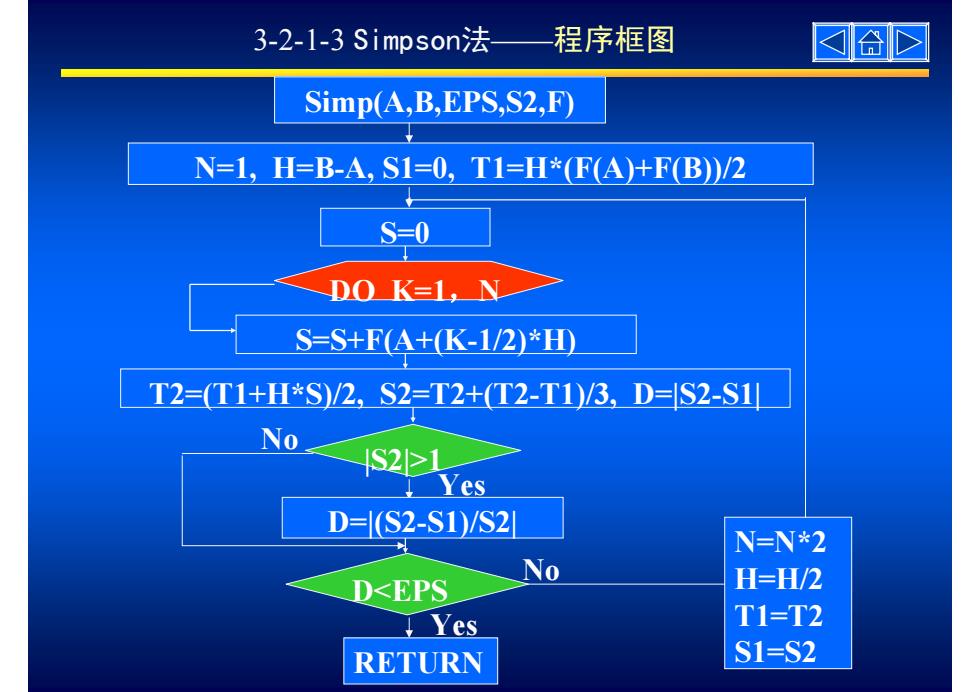
3-2-1-3 Simpsoni法 程序框图 合) Simp(A,B,EPS,S2,F) N=1,H=B-A,S1=0,T1=H*FA)+FB)/2 S=0 DO K=1,N S=S+F4+K-1/2)*H T2=(T1+H*S/2,S2=T2+T2-T1/3,D=S2-S1 No 1S2 Yes D=(S2-S1)/S2 N=N*2 No D<EPS H=H/2 Yes T1=T2 RETURN S1=S2
3-2-1-3 Simpson法——程序框图 Simp(A,B,EPS,S2,F) N=1, H=B-A, S1=0, T1=H*(F(A)+F(B))/2 DO K=1,N S=0 S=S+F(A+(K-1/2)*H) T2=(T1+H*S)/2, S2=T2+(T2-T1)/3, D=|S2-S1| |S2|>1 D=|(S2-S1)/S2| D<EPS No RETURN Yes No N=N*2 H=H/2 T1=T2 S1=S2 Yes

3-2-1-4 Simpsoni法 应用示例 国合 开始 输入:Debye温度T(5),精度EPS, 温度THETA 计算:XM=THETA/T四(I=1,N 输入:积分上下限A=104,B=XM Yes B=0 No 调用Simpson积分法子程序计算式右方积分值S2 固体的热容CV=9R公M*3*S2 输出:固体的热容Cy 显示程序 显示输出 结束 花
3-2-1-4 Simpson法——应用示例 开始 输入: Debye温度T(5),精度EPS,温度THETA 输出:固体的热容Cv 结束 调用Simpson积分法子程序计算式右方积分值S2 计算:XM=THETA/T(I) (I=1,N) 输入:积分上下限A=10-4,B=XM B=0 Yes No 固体的热容Cv=9R/XM**3*S2 显示程序 显示输出
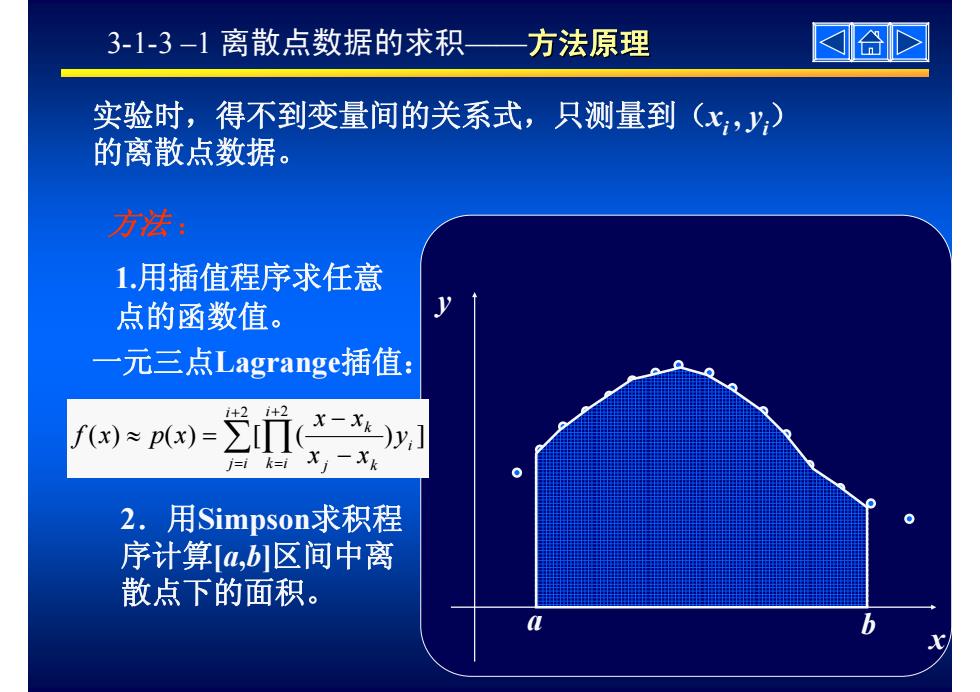
3-1-3-1离散点数据的求积一 方法原理 合正 实验时,得不到变量间的关系式,只测量到(xy) 的离散点数据。 方法: 1.用插值程序求任意 点的函数值。 一元三点Lagrange插值: i-m] 1+2 f()≈px)= 2.用Simpson:求积程 序计算a,b1区间中离 散点下的面积。 L
3-1-3 –1 离散点数据的求积——方法原理 实验时,得不到变量间的关系式,只测量到(xi , yi) 的离散点数据。 x y a b 方法 : 1.用插值程序求任意 点的函数值。 一元三点Lagrange插值: ∑ ∏ + = + = − − ≈ = 2 2 ( ) ( ) [ ( ) ] i j i i k i i j k k y x x x x f x p x 2.用Simpson求积程 序计算[a,b]区间中离 散点下的面积

3-1-3-2离散点数据的求积 程序框图 国合 Simp(M,A,B,X,Y,EPS,S2) N=1,H=B-A,(1);S1=0,T1=H*FA)tFB)/2 S=0 (①)调用 Lagrange DO K=L,N 元三点插值 F(A),F(B) (2);S=S+F4+K-1/2)山四 T2=(T1+H*S/2,S2=T2+(T2-T1)3,D=S2-S1] No S21 Yes D=S2-S1)/S2 N=N*2 No (2)调用Lagrange D<EPS H=H/2 一元三点插值 Yes T1=T2 F(A+(K-1/2)*H0 RETURN S1=S2
Simp(M,A,B,X,Y,EPS,S2) N=1, H=B-A, ( 1 ); S1=0, T1=H*(F(A)+F(B))/2 DO K=1 , N S=0 ( 2 ); S=S+F(A+(K-1/2)*H) T2=(T1+H*S)/2, S2=T2+(T2-T1)/3, D=|S2-S1| |S2|>1 D=|(S2-S1)/S2| D<EPS No RETURN Yes No N=N*2 H=H/2 T1=T2 S1=S2 Yes (1)调用 Lagrange 一 元三点插值 F(A),F(B) (2)调用Lagrange 一元三点插值 F(A+(K-1/2)*H) 3-1-3 –2 离散点数据的求积——程序框图