第三章数值积分与常微分方程的数值解法 合心 数值积分 1fx)函数形式已知,但其积 分不能表示成初等函数的闭 ●梯形法 合形式 ●Simpson:法 2.x)函数形式未知,但其 离散点数据的求积 离散数据表已给出 常微分方程的数值解法 ●Euler法及其改进 ● Runge-.Kutta法 合
● Euler法及其改进 ● Runge-Kutta法 ● 梯形法 ● Simpson法 ●离散点数据的求积 第三章 数值积分与常微分方程的数值解法 数值积分 常微分方程的数值解法 1.f(x)函数形式已知,但其积 分不能表示成初等函数的闭 合形式 2. f(x)函数形式未知,但其 离散数据表已给出
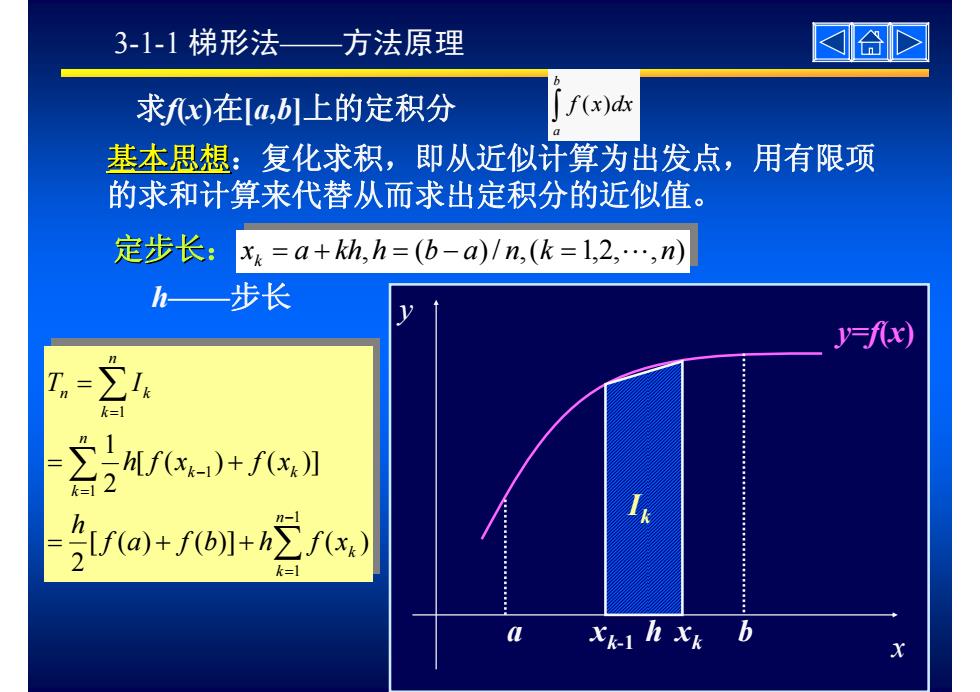
3-1-1梯形法— 方法原理 国合 求fx)在a,b]上的定积分 f(x)dx 基本思想:复化求积,即从近似计算为出发点,用有限项 的求和计算来代替从而求出定积分的近似值。 定步长: x=a+kh,h=(b-a)/n,(k=l,2,…,m) h—步长 y=fx) 2上Mfx-)+fx】 2 =经a)+fb+2f) k= Xk-1 h xk
3-1-1 梯形法——方法原理 基本思想:复化求积,即从近似计算为出发点,用有限项 的求和计算来代替从而求出定积分的近似值。 定步长: x a kh,h (b a)/ n,(k 1,2, ,n) k = + = − = L 求f(x)在[a,b]上的定积分 x y y=f(x) a b xk-1 h xk Ik ∑ ∑ ∑ − = = − = = + + = + = 1 1 1 1 1 [ ( ) ( )] ( ) 2 [ ( ) ( )] 21 n k k n k k k n k n k f a f b h f x h h f x f x T I ∫ b a f (x)dx h——步长
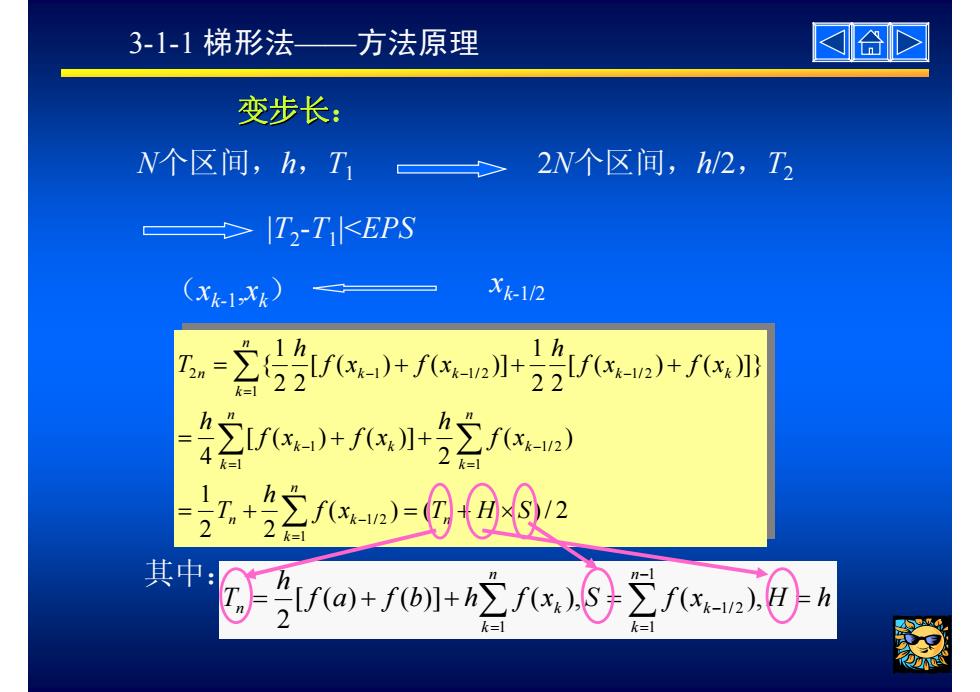
3-1-1梯形法 方法原理 合心 变步长: N个区间,h,T 2N个区间,h/2,T T-T K<EPS (Xk1xk》 Xk-112 五.-立2++2n+加 42f+x+2f) +2国@2 其中: 3/a)+16+2/x.③21x0A
变步长: N个区间,h,T1 2N个区间,h/2,T2 |T2-T1|<EPS (xk-1,xk) xk-1/2 ( ) ( )/ 2 2 2 1 ( ) 2 [ ( ) ( )] 4 [ ( ) ( )]} 2 2 1 [ ( ) ( )] 2 2 1{ 1 1/ 2 1 1 1 1/ 2 1 2 1 1/ 2 1/ 2 f x T H S h T f x h f x f x h f x f x h f x f x h T n n k n k n k n k k k k n k n k k k k = + = + × = + + = + + + ∑ ∑ ∑ ∑ = − = = − − = − − − 其中: f a f b h f x S f x H h h T n k k n k n = + + ∑ k = ∑ = − = − = [ ( ) ( )] ( ), ( ), 2 1 1 1/ 2 1 3-1-1 梯形法——方法原理

3-2-1-1 Simpson法 一问题的提出 国合 例:Debye--Einstein公式推导得到计算固体热容的公式为 Cr=9R/Xie'.xle"-1)dx 其中: Xm=0/T0,为Debye温度,R为气体常数8.314JK1mol1 已知固体的Debye温度如下: Pb Ag Cu Al Fe KCI NaCl a*K88 215 315 398 420 227 281 1910 求在50,100,298.15,500,1500K时,各固体的热容
例:Debye-Einstein公式推导得到计算固体热容的公式为 ∫ = ⋅ − m 0 3 4 2 m 9 / /( 1) d x x x V C R X e x e x 其中: X m =θ D /T θD为Debye温度,R为气体常数8.314J·K-1·mol-1 已知固体的Debye温度如下: θD/*K 88 215 315 398 420 227 281 1910 Pb Ag Cu Al Fe KCl NaCl C 求在50,100,298.15,500,1500K时,各固体的热容。 3-2-1-1 Simpson法——问题的提出

3-2-1-2 Simpsoni法 —方法原理 可合戊 求积分 S-jrcd Simpson法是把积分区间分割成有限个小区间,在每个小 区间上采用二次抛物线来近似被积函数x)的图形,近似求出 小区间的面积,然后再将有限个小区间相加得到被积函数的 近似值。 y=f(x) 定步长 y=g(x) h=(b-a)/2n =(px =身x)+4x+0++2 xil h xi h xi-l
求积分 ∫ = b a S f (x)dx Simpson法是把积分区间分割成有限个小区间,在每个小 区间上采用二次抛物线来近似被积函数f(x)的图形,近似求出 小区间的面积,然后再将有限个小区间相加得到被积函数的 近似值。 x y y=f(x) xi-1 xi xi+1 y=g(x) h h Si 定步长: h = (b − a)/ 2n [ ( ) 4 ( ) ( 2 )] 3 ( )d 2 2 f x f x h f x h h S px qx r x i i i x h x i i i = + + + + = + + ∫ + 3-2-1-2 Simpson法——方法原理