第一章代数方程及代数方程组的求解在化学中的应用 直接法 N<3 元N次非线性 二分法 弦截法 方程的求解 间接法 ★ 牛顿迭代法 插值法 直接法 Gauss:消去法 线性方程组 的求解 ★ 间接法 Gauss--Seidel迭代法
第一章 代数方程及代数方程组的求解在化学中的应用 一元N次非线性 方程的求解 线性方程组 的求解 直接法 间接法 直接法 间接法 N<3 二分法 弦截法 牛顿迭代法 插值法 Gauss消去法 Gauss-Seidel迭代法 ★ ★ ★ ★ P11

1-1-1-1二分法- 问题的提出 例:压力对化学反应中反应物平衡转化率的影响 任何气相化学反应 0=∑mB 达平衡时有 ∑YB4阳=0 ■ 里 aA+bB=cC+dD 里 起始nB./mol a b 0 0 里 平衡ng/mola(1-x) b(1-x) Cr dx 置 >n/mol=a(1-x)+b(1-x)+x+d =(-a-b+c+d)x+(a+b) =(∑yB)x+n
1-1-1-1 二分法——问题的提出 例:压力对化学反应中反应物平衡转化率的影响 任何气相化学反应 达平衡时有 B 0 B = ∑γ ∑ = 0 Bμ B γ ab cd A B = C D + + B B 0 / (1 ) (1 ) ( )( ) ( ) n mol a x b x cx dx a b c dx a b γ x n = −+ −++ = −−++ + + = + ∑ ∑ 起始nB,0/mol a b 0 0 平衡nB/mol a(1-x) b(1-x) cx dx

1-1-1-1二分法 问题的提出 温度一定,0为常数,平衡时,0与总压之间关系为: 即 K0= (cx)°.(dx) [a(1-x)][b(1-x)] 2p c+d (1-一9*6 ∑n 令 画 SRa+b≥(∑Y)反应物 SP=c+d=(∑y)产物 =Π B 上式整理为: -x)sR=K0 ∑YB1KN (1
温度一定,K0为常数, 平衡时,K0与总压p之间关系为: ∑ = ∑ B ( ) 0 B 0 γ n p p K Kn 即 B B 0 0 B 0 B ()( ) ( ) [ (1 )] [ (1 )] / ( ) (1 ) c d a b cd c d ab a b cx dx p K a x b x np x c d pp x ab n γ γ + + ⋅ ∑ = − ⋅− ⋅ ∑ = ⋅ − ⋅ ∑ ∑ 令 B B B () () c d a b SR a b SP c d c d KN a b γ γ γ γ = + =− = + = ⋅ = = ⋅ ∑ ∑ ∏ 反应物 产物 上式整理为: KN p p n K x x SR SP ) / / ( (1 ) B 0 0 B ∑ = − ∑ γ 1-1-1-1 二分法——问题的提出

1-1-1-1二分法- 问题的提出 令 F(x)= 此方程为含x的高次方程,x:0.0~1.0之间用二分法
令 ) / 0 / ( (1 ) ( ) B 0 0 B = ∑ − − = ∑ KN p pn K x x F x SR SP γ 此方程为含x的高次方程,x:0.0~1.0之间 用二分法 1-1-1-1 二分法——问题的提出
1-1-1-2二分法— 方法原理 有函数fx)=0,求在区间[a,b]内的实根。 设:①函数fx)在区间[a,b内连续。 画 ②函数在a、b两点之值孔a)与fb)异号,说明在 区间[,b]中至少有一实根。 里 可得一 系列区间套: 围 Ax) (ab)(ab)(a,b)c(a,b) 它们必须满足: 1x2 画 Xo b f(an)·f(bn)<0 b-a bn-an= 22
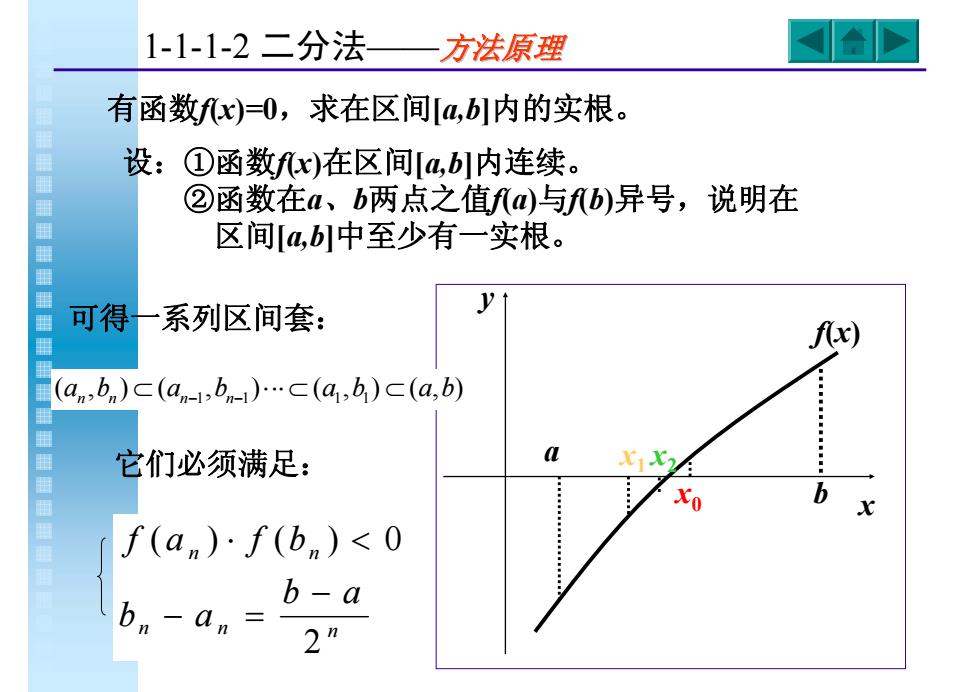
有函数f(x)=0,求在区间[a,b]内的实根。 设:①函数f(x)在区间[a,b]内连续。 ②函数在a、b两点之值f(a)与f(b)异号,说明在 区间[a,b]中至少有一实根。 a x0 b x1 可得一系列区间套: ( , ) ( , ) ( , ) ( , ) 1 1 1 1 a b a b a b a b n n ⊂ n− n− ⋅⋅⋅ ⊂ ⊂ 它们必须满足: n n n n n b a b a f a f b 2 ( ) ( ) 0 − − = ⋅ < x y f(x) x2 1-1-1-2 二分法——方法原理