2.1平面汇交力系 例题1讨论 1若希望通过列一个平衡方程求1杆的力如何设投影轴? 2若希望通过列一个平衡方程求2杆的力如何设投影轴? 3保持杆件位置不变,若力F的方位可以变化,力沿 什么方位1杆的受力为零? 4保持杆件位置不变,力F力沿什么方位2杆的受力为零 5保持杆件的位置不变,什么情况下。两个杆的受力都 等于零? 2
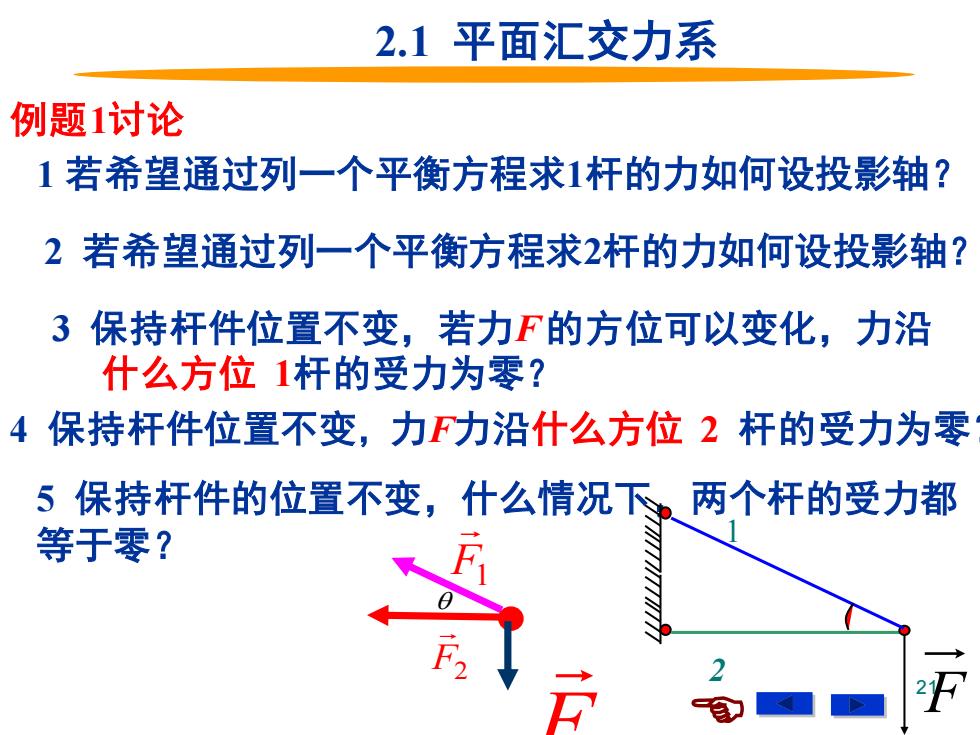
21 1 若希望通过列一个平衡方程求1杆的力如何设投影轴? 2 若希望通过列一个平衡方程求2杆的力如何设投影轴? 3 保持杆件位置不变,若力F 的方位可以变化,力沿 什么方位 1杆的受力为零? 4 保持杆件位置不变,力F力沿什么方位 2 杆的受力为零? 5 保持杆件的位置不变,什么情况下,两个杆的受力都 等于零? 2.1 平面汇交力系 例题1讨论 F1 F F2 1 2 F

2.2平面力对点之矩平面力偶 力对点之矩(力矩) 1代数量?2如何表示? M(F) 简称为矩心 3正负规定:力使物体绕矩心逆时针转动时为正, 反之为负。 M(F)=±fh 力臂 力F使物体绕矩心A顺时针转动 M(F)=-Fh 当力臂不方便求如何求解? 22
22 ( ) MO F M F Fh A ( ) = − 一 力对点之矩(力矩) 1 代数量? 2 如何表示? 简称为矩心 3 正负规定:力使物体绕矩心逆时针转动时为正, 反之为负。 ( ) M Fh O F = A B C F 力臂 h 力F使物体绕矩心A顺时针转动 当力臂不方便求如何求解? 2.2 平面力对点之矩 平面力偶
平面力对点之矩 4合力矩定理 平面直角折杆 ■■■■■■■ AB=L BC=a 风无法显示该图片。 M,(F))=-FL+F,a =-F cosOL+Fsin Q Mo(FR)=∑M(F) i=1 平面汇交力系的合力对于平面内任一点之矩等于 所有各分力对于该点之矩的代数和。 23
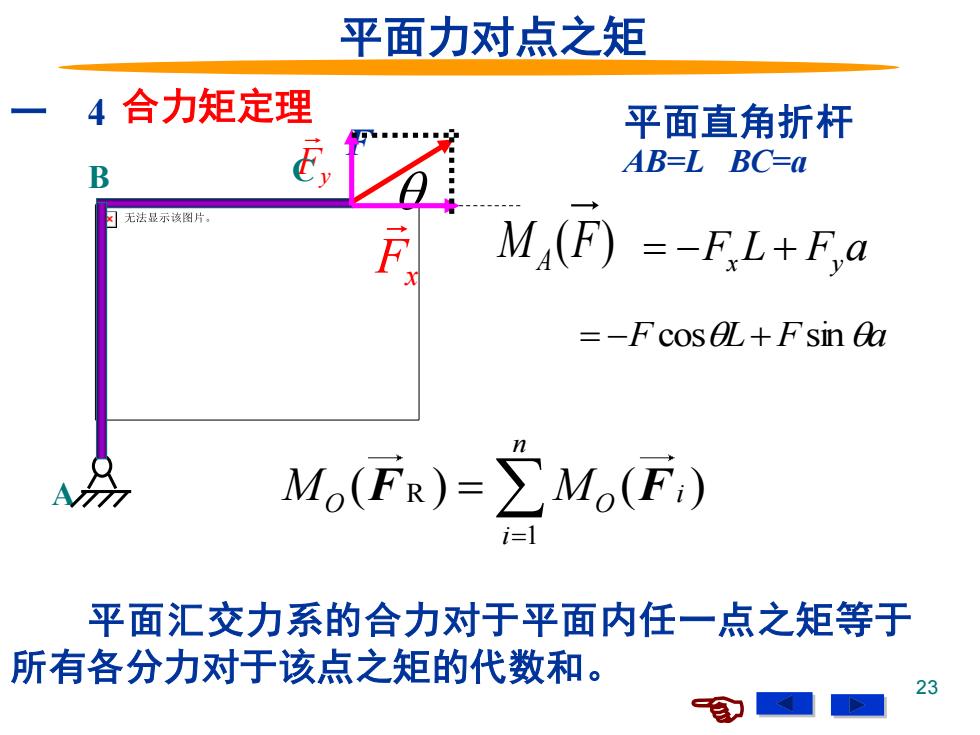
23 = −Fx L + Fy a = −F cosL+ Fsina Fy Fx 平面力对点之矩 一 4 A B C F M (F) A 平面直角折杆 AB=L BC=a 合力矩定理 平面汇交力系的合力对于平面内任一点之矩等于 所有各分力对于该点之矩的代数和。 R 1 ( ) ( ) n i O O i M M = F F =
2.2平面力对点之矩平面力偶 一 、5力矩的解析表达式 平面汇交力系的合力对于平面内任一点之矩等于 所有各分力对于该点之矩的代数和。 M(FR)=∑M(F) P342-11式 Mo(F)=Fsin cos0 注意:上述公式中的每一项都是在正的情况下给出的 24
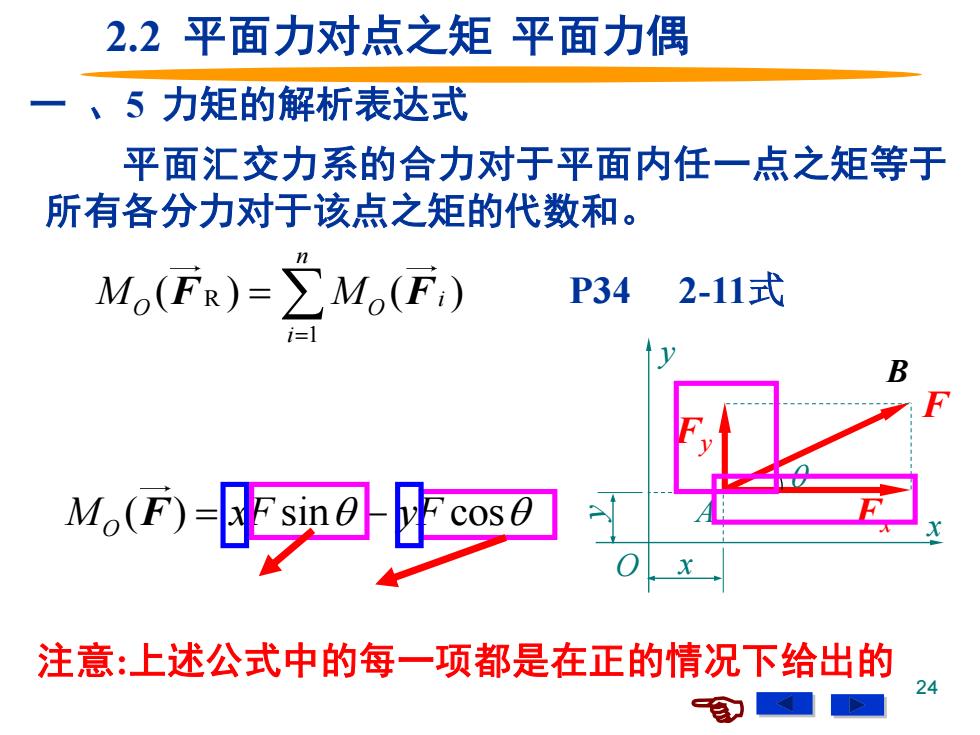
24 平面汇交力系的合力对于平面内任一点之矩等于 所有各分力对于该点之矩的代数和。 R 1 ( ) ( ) n i O O i M M = F F = F Fx Fy x y O x ( ) sin cos y A O y x M xF yF xF yF = − = − F 力矩的解析表达式 注意:上述公式中的每一项都是在正的情况下给出的 P34 2-11式 2.2 平面力对点之矩 平面力偶 B 一 、5
2.2平面力对点之矩平面力偶 二力偶和力偶矩 1力偶 M(F,F) 由两个大小相等、方向相反且不共线的平行力组成 的力系,称为力偶,记为 力偶的两力之间的垂直距离d称为力偶臂 力偶所在的平面称为力偶作用面 力偶对物体只产生转动效应 25
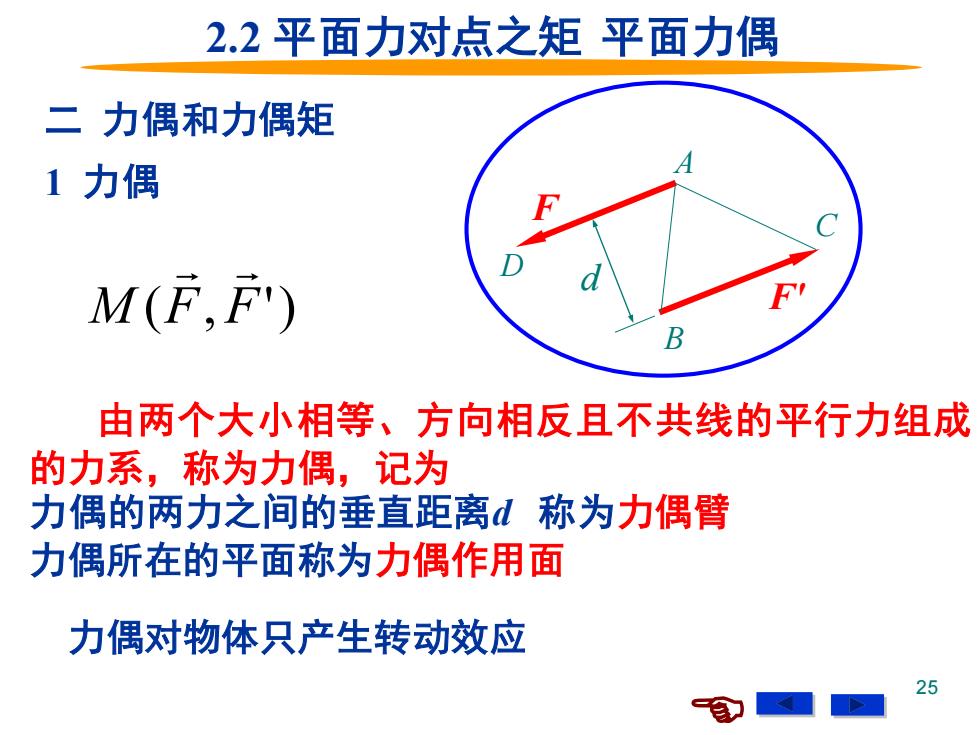
25 2.2 平面力对点之矩 平面力偶 由两个大小相等、方向相反且不共线的平行力组成 的力系,称为力偶,记为 力偶的两力之间的垂直距离d 称为力偶臂 力偶所在的平面称为力偶作用面 二 力偶和力偶矩 力偶对物体只产生转动效应 F F' d D A B C 1 力偶 M (F, F')