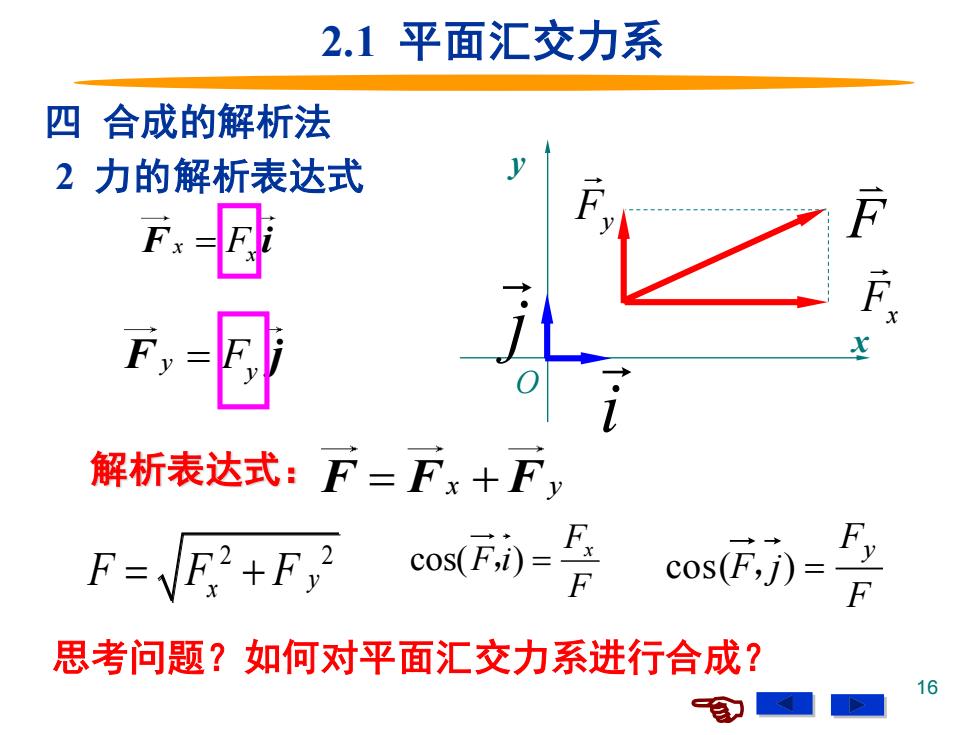
2.1平面汇交力系 四合成的解析法 2力的解析表达式 F为 E 解析表达式:F=Fx十Fy F=+F厚0=长oc=号 思考问题?如何对平面汇交力系进行合成? 16
16 2 力的解析表达式 x F i = F x y F j = F y F F F i x cos( ,) = x y F F F i j = + = + F F x y x y O 2 2 y F F F = + x 解析表达式: F F F j y cos( ,) = 2.1 平面汇交力系 四 合成的解析法 i j F Fx Fy 思考问题?如何对平面汇交力系进行合成?

2.1平面汇交力系 四合成的解析法 3合矢量的投影定理 合矢量在某轴上的投影,等于各个分矢量在同一 轴上投影的代数和 P31 i= 4合成FR=2+(F2-②F,2+(②F,)2 cos(F= os(Fg:j)= FRy FR FR 1> -
17 3 合矢量的投影定理 R 1 n y yi i F F = = R Ry R F F cos(F ,j) = R 1 n x xi i F F = = 合矢量在某轴上的投影,等于各个分矢量在同一 轴上投影的代数和 2.1 平面汇交力系 四 合成的解析法 4 合成 P31 R Rx R F F cos(F ,i) = 2 2 2 2 = ( ) + ( ) = ( ) + ( ) i FR FRx FRy Fxi Fy

2.1平面汇交力系 五平衡方程 FR=VE)子+(E=EE,}+(②万,卫 FR=V∑F)2+(∑F)2=0 ∑F=0 ∑F=0 1平衡的必要和充分条件是:各力在作用面内两 个任选的坐标轴上投影的代数和等于零 2上式称为平面汇交力系的平衡方程 注意:独立的平衡方程的数目为2 18
18 五 平衡方程 2 2 R ( ) ( ) 0 F F F = + = xi yi 0 0 xi yi F F = = 1 平衡的必要和充分条件是:各力在作用面内两 个任选的坐标轴上投影的代数和等于零 2 上式称为平面汇交力系的平衡方程 注意:独立的平衡方程的数目为2 2.1 平面汇交力系 2 2 2 2 = ( ) + ( ) = ( ) + ( ) i FR FRx FRy Fxi Fy
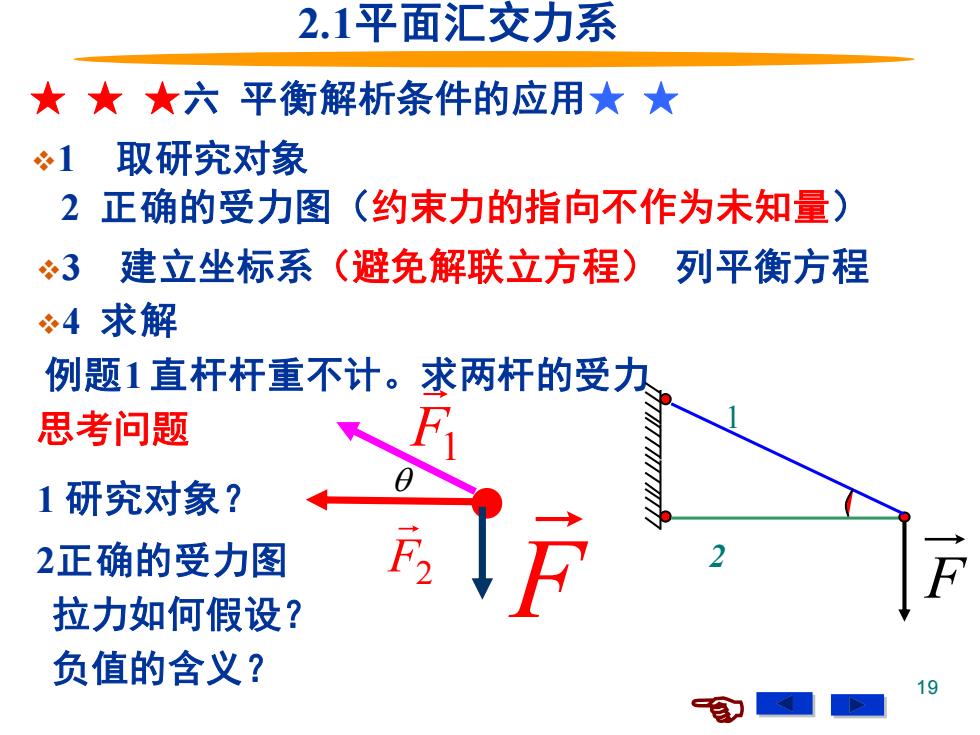
2.1平面汇交力系 ★★★六平衡解析条件的应用★★ 冬1取研究对象 2正确的受力图(约束力的指向不作为未知量) 3建立坐标系(避免解联立方程) 列平衡方程 4求解 例题1直杆杆重不计。求两杆的受力 思考问题 F 1研究对象? 2正确的受力图 拉力如何假设? 负值的含义?
19 F1 F F2 2.1平面汇交力系 ★ ★ ★六 平衡解析条件的应用★ ★ ❖1 取研究对象 2 正确的受力图(约束力的指向不作为未知量) ❖3 建立坐标系(避免解联立方程) 列平衡方程 ❖4 求解 例题1 直杆杆重不计。求两杆的受力 思考问题 1 研究对象? 2正确的受力图 拉力如何假设? 负值的含义? 1 2 F

六女女★平衡解析条件的应用★★ 例题1直杆杆重不计。求两杆的受力 ∑F=0 -F3-Ec0s0=0.1) ∑F=0 Esin0-F=0.2) F F= F2 =-Fctg0 sin0 负值的含义? F 杆2所受的力为压力根据作用力反作用力定律 杆1所受的力为拉力 ÷1取研究对象 2正确的受力图 杆2所受的力为压力3建立坐标系列平衡方程 4求解 20
20 Fx = 0 cos 0. 1) −F2 − F1 = Fy = 0 sin 0. 2) F1 − F = sin 1 F F = F2 = −Fctg F1 F F2 ❖1 取研究对象 例题1 直杆杆重不计。求两杆的受力 六 ★ ★ ★平衡解析条件的应用★ ★ 负值的含义? 杆2所受的力为压力 2 正确的受力图 ❖3 建立坐标系列平衡方程 ❖4 求解 根据作用力反作用力定律 杆1所受的力为拉力 杆2所受的力为压力 1 2 F