
热力学稳定性和反应的自发性 一热力学稳定性和动力学稳定性 无机化学中讨论元素及化合物的性质时,其中一个中心问题 就是化学体系的稳定性。 如,某元素能否形成某种化合物,这要看该化合物能否在一 定条件下稳定存在。在研究一个合成反应是否可行时,也可把问 题归结为有关反应物体系是否稳定。因而可以说,无机化学里的 一个重要问题是试图去说明不同化学体系的稳定性。 一 般地说,一个体系是稳定的,即表观上不随时间而变化。 物理化学上把稳定的体系划分为两类,一类是真正稳定的,另 类是表观稳定的。前者是体系处于平衡状态,在该条件下体系中 的各种可能变化都不能自发进行。如CaCO,在常温下既不能分解 为CaO和C0,也不能分解为C、O,和Ca单质。另一种不是处于平衡 状态,而只是表观上稳定,即至少有一种可能的变化会自发进行, 只是变化的速率十分缓慢,以致不可能测量出来。如H,、O,的混 食入凳车室得景赛型a路长&小o智一释碧 性是由热力学因素所控制,称为热力学稳定性;,后一种稳定性是 由动力学因素 速率所控制,称为动力学稳定性
热力学稳定性和反应的自发性 一 热力学稳定性和动力学稳定性 无机化学中讨论元素及化合物的性质时,其中一个中心问题 就是化学体系的稳定性。 如,某元素能否形成某种化合物,这要看该化合物能否在一 定条件下稳定存在。在研究一个合成反应是否可行时,也可把问 题归结为有关反应物体系是否稳定。因而可以说,无机化学里的 一个重要问题是试图去说明不同化学体系的稳定性。 一般地说,一个体系是稳定的,即表观上不随时间而变化。 物理化学上把稳定的体系划分为两类,一类是真正稳定的,另一 类是表观稳定的。前者是体系处于平衡状态,在该条件下体系中 的各种可能变化都不能自发进行。如CaCO3在常温下既不能分解 为CaO和CO2 ,也不能分解为C、O2和Ca单质。另一种不是处于平衡 状态,而只是表观上稳定,即至少有一种可能的变化会自发进行, 只是变化的速率十分缓慢,以致不可能测量出来。如H2、O2的混 合气体在室温下是稳定的,可以长久共存。然而一旦将一块铂箔 放入其中,立即就会发生猛烈的反应,化合成H2O。前一种稳定 性是由热力学因素所控制,称为热力学稳定性;后一种稳定性是 由动力学因素——速率所控制,称为动力学稳定性

对任一个化学反应,其稳定性可由反应的平衡常数来判断。 如果平衡常数K值很小,则反应只要生成极少量产物就达到了平衡 态(此时反应物和产物的量不再变化),反应物的量接近于原始量, 此时,我们认为该反应物是稳定的。反之,K值很大,达到平衡时, 反应物几乎完全转变成了产物,那么反应物当然是不稳定的。 平衡常数K与反应的标准自由焓变化△G有如下关系式: △G=-RTInK 因此,△G的大的正值,意味着非常小的平衡常数,对于产 物的生成来说,反应物是热力学稳定的,因为达到平衡时,仅有 非常少量的产物生成。相反,△Gm大的负值意味着大的平衡常数, 这样一来,必须消耗相当量的反应物去生成产物才能达到平衡, 所以反应物是不稳定的。若△G=0,K=1,意味着体系处于一种 特定的状态,反应物和产物的量都不再随时间而改变。 一个反应的△Gm可通过以下关系式求得。 已知AL和△,Sm,△,G。=△H-TA,Sm9 已知各物种的△Gm9△,Gm=∑n△Gm(产)一∑n,△Gm(反) m 已知标准电动势,△,Gm9=一nl
对任一个化学反应,其稳定性可由反应的平衡常数来判断。 如果平衡常数K值很小,则反应只要生成极少量产物就达到了平衡 态(此时反应物和产物的量不再变化),反应物的量接近于原始量, 此时,我们认为该反应物是稳定的。反之,K值很大,达到平衡时, 反应物几乎完全转变成了产物,那么反应物当然是不稳定的。 平衡常数K与反应的标准自由焓变化△rGm θ有如下关系式: △rGm θ=-RTlnK 因此,△rGm θ的大的正值,意味着非常小的平衡常数,对于产 物的生成来说,反应物是热力学稳定的,因为达到平衡时,仅有 非常少量的产物生成。相反,△rGm θ大的负值意味着大的平衡常数, 这样一来,必须消耗相当量的反应物去生成产物才能达到平衡, 所以反应物是不稳定的。若△Gθ=0,K=1,意味着体系处于一种 特定的状态,反应物和产物的量都不再随时间而改变。 一个反应的△rGm θ可通过以下关系式求得。 已知△rHm θ和△rSm θ , △rGm θ=△rHm θ-T△rSm θ 已知各物种的△fGm θ , △rGm θ=∑nj△fGm θ (产)-∑ni△fGm θ (反) 已知标准电动势,△rGm θ=-nFEθ

可见用△G来判断一个反应体系的稳定性与用K来判断是 回事。 严格地说必须用△G来进行判断,原因是△G所指的反应 物和生成物都处于标准态,或虽不是标准态,但反应熵Q=1这样 的特定条件下的自由焓变化值,而在实际情况是,反应物和产 物都未必都是处于这种状态。 但是根据等温式△Gnm=△Gm+RTlnQ,如果△G的绝对 值十分大,则△Gm的正负号就基本上决定了△Gn的符号。即, 若△Gm的负值很大,一般情况下,△Gm大致也是负值,要使 △G改变符号就必须使Q变得很大,这在实际上有时是难以办 到的。如在298K时,反应 Zn(s)+1/2O2(g)=Zn0(s) △,Gm9=-318.3 kJ.mol-1 根据△,Gn=-RTlnK,K=[1/{p(O2)/P]2, 解出p(02)=2.82×10-107Pa。 即要使此反应不能正向进行,则应使Q>K,即要使(O,)如此 地低,这是难以办到的,在通常情况下,p(O)总是大于这个值 *△,Gm只决定于反应的始态和终态,即热力学稳定性与反应途 径或机理无关
可见用△rGm θ*来判断一个反应体系的稳定性与用K来判断是 一回事。 严格地说必须用△G来进行判断,原因是△rGm θ所指的反应 物和生成物都处于标准态, 或虽不是标准态, 但反应熵Q=1这样 的特定条件下的自由焓变化值,而在实际情况是,反应物和产 物都未必都是处于这种状态。 但是根据等温式△rGm =△rGm θ+RTlnQ,如果△rGm θ的绝对 值十分大,则△rGm θ的正负号就基本上决定了△rGm的符号。即, 若△rGm θ的负值很大,一般情况下,△rGm大致也是负值,要使 △rGm改变符号就必须使Q变得很大,这在实际上有时是难以办 到的。如在298K时,反应 Zn(s)+1/2 O2 (g)=ZnO(s) △rGm θ=-318.3 kJ·mol-1 根据 △rGm θ=-RTlnKθ ,K=[1/{p(O2 ) /Pθ}]1/2 , 解出 p(O2 )=2.82×10-107 Pa。 即要使此反应不能正向进行, 则应使Q>K, 即要使p(O2 )如此 地低,这是难以办到的,在通常情况下,p(O2 ) 总是大于这个值。 *△rGm θ只决定于反应的始态和终态,即热力学稳定性与反应途 径或机理无关

同理,如果△Gm的正值很大,也很难通过改变Q的数值使 △Gn的符号与△Gn相反。 因此,当△G的绝对值很大时,可以用△G的值来判断 反应的方向。 习惯上人们把△Gm<-40 kJmol-1和>40 kJ.moli-1分别作为 反应可能是自发和不可能是自发进行,或反应物是不稳定的或稳 定的判断依据。如果-40<△,G<40,就存在可能通过改变Q值 时平衡向所需方向进行的可能性。 如在298K时,反应NH,Cl(s)一NH,(g)+HCl(g)△G=92.3 kJ.mol-1。认为在这时NH,CI是不能自发分解的或NH,CI是稳定的。 但是,对于NH,HCO,(s)一→NH3+HO(g)+CO2,△G=31.1 kJ.mol-1,处于-40和40之间,假定pNH3)=pH2O)=p(C02)= 1.01325×105Pa时,NH,HCO3在室温下不分解;但是若改变这三 者的压力,如分别变为0.01×1.01325×105Pa,则 △G=△G+RTInQ 0.01×1.01325×1053 =31.1+8.315×10-3×298×1n 1.01325×105 =-3.1 kJ.mol-1<0。 所以在此条件下,NH,HCO,就可以分解了
同理,如果△rGm θ的正值很大,也很难通过改变Q的数值使 △rGm的符号与△rGm θ相反。 因此,当△rGm θ的绝对值很大时,可以用△rGm θ的值来判断 反应的方向。 习惯上人们把△rGm θ<-40 kJ·mol-1和 >40 kJ·mol-1分别作为 反应可能是自发和不可能是自发进行,或反应物是不稳定的或稳 定的判断依据。如果-40<△rGm θ<40,就存在可能通过改变Q值 时平衡向所需方向进行的可能性。 如在298K时,反应 NH4Cl(s) NH3 (g)+HCl(g) △Gθ=92.3 kJ·mol-1 。认为在这时NH4Cl是不能自发分解的或NH4Cl是稳定的。 但是,对于NH4HCO3 (s) NH3+H2O(g)+CO2 , △Gθ=31.1 kJ·mol-1 ,处于-40和40之间,假定p(NH3 )=p(H2O)=p(CO2 )= 1.01325×105Pa时,NH4HCO3在室温下不分解;但是若改变这三 者的压力,如分别变为0.01×1.01325×105Pa,则 △G=△Gθ+RTlnQ =31.1+8.315×10-3×298×ln =-3.1 kJ·mol-1 <0。 所以在此条件下,NH4HCO3就可以分解了。 0.01×1.01325×105 1.01325×105 3
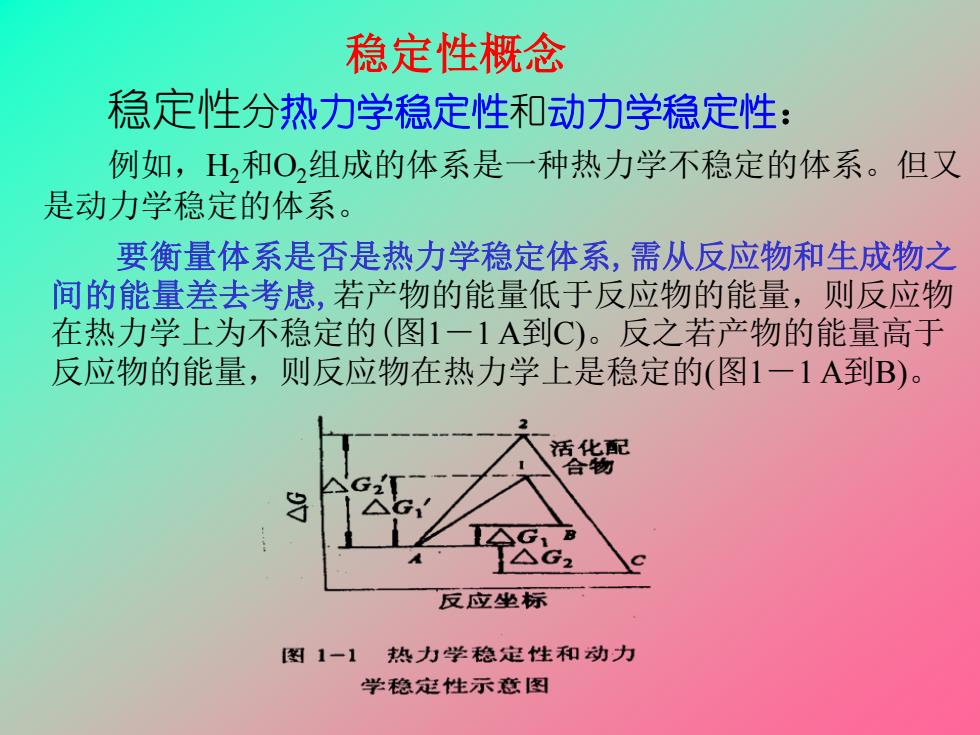
稳定性概念 稳定性分热力学稳定性和动力学稳定性: 例如,H和O组成的体系是一种热力学不稳定的体系。但又 是动力学稳定的体系。 要衡量体系是否是热力学稳定体系,需从反应物和生成物之 间的能量差去考虑,若产物的能量低于反应物的能量,则反应物 在热力学上为不稳定的(图1一1A到C)。反之若产物的能量高于 反应物的能量,则反应物在热力学上是稳定的(图1一1A到B)。 活化配 合物 反应坐标 图1-1 热力学稳定性和动力 学稳定性示意图
要衡量体系是否是热力学稳定体系,需从反应物和生成物之 间的能量差去考虑,若产物的能量低于反应物的能量,则反应物 在热力学上为不稳定的(图1-1 A到C)。反之若产物的能量高于 反应物的能量,则反应物在热力学上是稳定的(图1-1 A到B)。 稳定性分热力学稳定性和动力学稳定性: 例如,H2和O2组成的体系是一种热力学不稳定的体系。但又 是动力学稳定的体系。 稳定性概念