
2.1.2平行投影(正投影)的基本性质 (1)平行性:如果空间直线平行,则它们的投影仍然互相平行。 (2)从属性:几何元素的空间从属关系在投影中不会发生改变; 从属于直线的点的投影必定落在直线的同面投影上,属于 面的点和线的投影必定落在平面的同面投影上。 (3)定比性:若空间直线上一点把该直线分成两段,则该两线 段之比,必等于其投影比;空间平行线段的长度之比,等 于其投影之比
(1)平行性:如果空间直线平行,则它们的投影仍然互相平行。 (2)从属性:几何元素的空间从属关系在投影中不会发生改变; 从属于直线的点的投影必定落在直线的同面投影上,属于 面的点和线的投影必定落在平面的同面投影上。 (3)定比性:若空间直线上一点把该直线分成两段,则该两线 段之比,必等于其投影比;空间平行线段的长度之比,等 于其投影之比。 2.1.2平行投影(正投影)的基本性质

(2)积聚性 当一线段与投影面垂直时,其正投影积聚为一点 当一平面图形与投影面垂直时其正投影积聚为一直线。 积聚成一点 积聚成一直线 歌 为配
当一平面图形与投影面垂直时其正投影积聚为一直线。 ⑵ 积聚性 当一线段与投影面垂直时,其正投影积聚为一点
(4)真实性、实形性 当一线段与投影面平行时,其正投影反映该线 段的实际长度 实际长度 实际形状 B 歌 钱郭
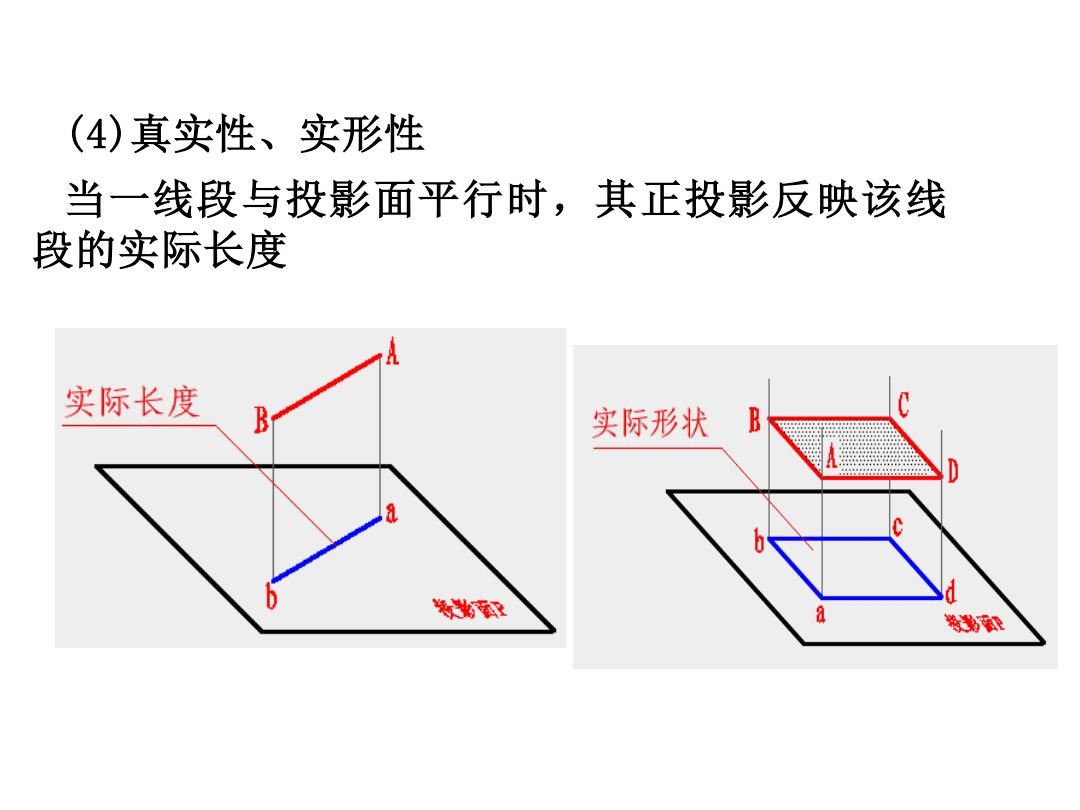
(4)真实性、实形性 当一线段与投影面平行时,其正投影反映该线 段的实际长度
(5)类似性 当一线段与投影面成倾斜时,其正投影缩短 当一平面图形与投影面成倾斜时,其正投影为缩小的类 似图形。 投影缩短 图形缩小
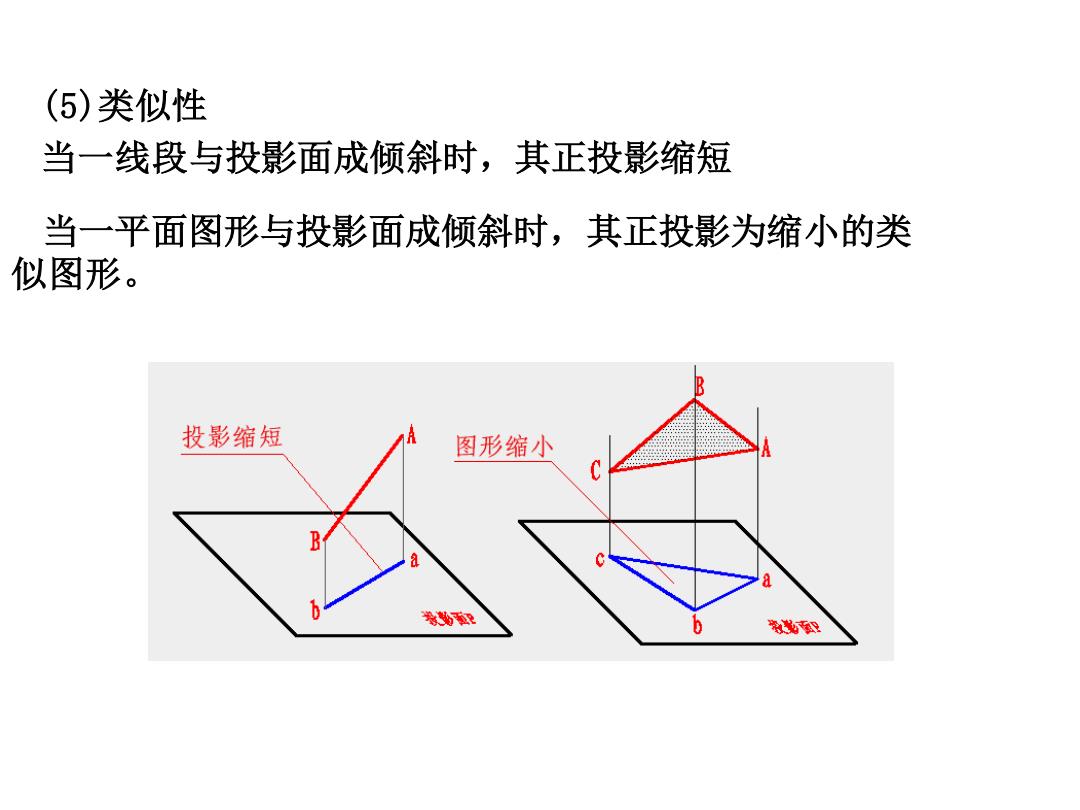
当一平面图形与投影面成倾斜时,其正投影为缩小的类 似图形。 (5)类似性 当一线段与投影面成倾斜时,其正投影缩短

归纳正投影的三个特性如下: 1.当几何要素与投影面平行时一一其投影表现出真 实性 2.当几何要素与投影面垂直时一一其投影表现出积 聚性 3.当几何要素与投影面倾斜时一一其投影表现出类 似性
归纳正投影的三个特性如下: 1.当几何要素与投影面平行时——其投影表现出真 实性 2.当几何要素与投影面垂直时——其投影表现出积 聚性 3.当几何要素与投影面倾斜时——其投影表现出类 似性