
Matlab与通信仿真 14
Matlab 与通信仿真 14

Matlab与通信仿真 实验三 随机信号与数字基带实验 一、实验目的 ●掌握库函数产生随机数方法 ●基带信号波形生成和其功率谱密度 ●理解采用蒙特卡罗算法仿真的思想 二、实验原理 (一).库函数产生随机数 ①均匀分布的随机数 利用MATLAB库函数rand产生。rand函数产生(0,I)内均匀分布的随机数,使用方法 如下: 1)x=rand(m);产生一个m×m的矩阵,所含元素取值均为在(0,1)内均匀分布的随机 数。 2)xand(m,n);产生一个m×n的矩阵,所含元素取值均为在(0,1)内均匀分布的 随机数。 3)x=rand;产生一个随机数。 4)调用rand(1,0给出均值为0.5,功率为1/12-0.083的白噪声。 5)调用rand(1,0给出均值为0.5,功率为o2=0.083的白噪声,现在要均值为0,功 率为0.01。 ②高斯分布的随机数 randn函数产生均值为0,方差为1的高斯分布的随机数,使用方法如下: 1)x=randn(m);产生一个mXm的矩阵,所含元素都是均值为0,方差为1的高斯分布的 随机数。 2)x可andn(m,n);产生一个m×n的矩阵,所含元素都是均值为0,方差为1的高斯分 布的随机数。 3)x=randn;产生一个均值为0,方差为1的高斯分布的随机数。 4)调用randn,生成均值为0,方差为1,服从高斯分布的白噪声信号u(n)。 (二).基带信号波形生成和信号的功率谱密度 1).要画出完整的基带信号波形,每一个码元要采n个样值。 2)信号f(t)的功率谱密度为:P(o)=1im F(@) T (三).蒙特卡罗算法 蒙特卡罗估计是指通过随机实验估计系统参数值的过程。蒙特卡罗算法的基本思想:由 概率论可知,随机实验中实验的结果是无法预测的,只能用统计的方法来描述。故需进行大 量的随机实验,如果实验次数为N,以N,表示事件A发生的次数。若将A发生的概率近似 15
Matlab 与通信仿真 15 实验三 随机信号与数字基带实验 一、实验目的 ⚫ 掌握库函数产生随机数方法 ⚫ 基带信号波形生成和其功率谱密度 ⚫ 理解采用蒙特卡罗算法仿真的思想 二、实验原理 (一).库函数产生随机数 ① 均匀分布的随机数 利用 MATLAB 库函数 rand 产生。rand 函数产生(0,1)内均匀分布的随机数,使用方法 如下: 1)x=rand(m);产生一个 m×m 的矩阵,所含元素取值均为在(0,1)内均匀分布的随机 数。 2)x=rand(m,n);产生一个 m×n 的矩阵,所含元素取值均为在(0,1)内均匀分布的 随机数。 3)x=rand;产生一个随机数。 4)调用 rand(1,N)给出均值为 0.5,功率为 1/12=0.083 的白噪声。 5)调用 rand(1,N)给出均值为 0.5,功率为 2 0.083 n = 的白噪声,现在要均值为 0,功 率为 0.01。 ② 高斯分布的随机数 randn 函数产生均值为 0,方差为 1 的高斯分布的随机数,使用方法如下: 1)x=randn(m);产生一个 m×m 的矩阵,所含元素都是均值为 0,方差为 1 的高斯分布的 随机数。 2)x=randn(m,n);产生一个 m×n 的矩阵,所含元素都是均值为 0,方差为 1 的高斯分 布的随机数。 3)x=randn;产生一个均值为 0,方差为 1 的高斯分布的随机数。 4)调用 randn,生成均值为 0,方差为 1,服从高斯分布的白噪声信号 u(n)。 (二).基带信号波形生成和信号的功率谱密度 1).要画出完整的基带信号波形,每一个码元要采 n 个样值。 2)信号 f (t) 的功率谱密度为: T F P l im T T 2 ( ) ( ) → = 。 (三).蒙特卡罗算法 蒙特卡罗估计是指通过随机实验估计系统参数值的过程。蒙特卡罗算法的基本思想:由 概率论可知,随机实验中实验的结果是无法预测的,只能用统计的方法来描述。故需进行大 量的随机实验,如果实验次数为 N ,以 NA 表示事件 A 发生的次数。若将 A 发生的概率近似

Matlab与通信仿真 为相对频率,定义为N,/N。这样,在相对频率的意义下,事件A发生的概率可以通过重复 N多 无限多次随机实验来求得,即:P(4)=lim 在二进制数字通信系统中,若N是发送端发送的总码元数,N,是差错发生的次数,则 总误码率可通过蒙特卡罗算法计算。 三、实验内容 1.产生随机数。 利用rand函数产生5×4的(0,2)内均匀分布的随机数: 利用randn函数产生5X4的均值为0,方差为2的高斯分布的随机数。 2.利用随机数产生单极性基带信号,每一个码元要采8个样值,并画出其波形和功率谱密。 3.利用蒙特卡罗算法仿真二进制双极性基带通信系统的误码率。 假定通信系统满足以下条件: ①信源输出的数据符号是相互独立和等概的双极性基带信号 ②发送端没有发送滤波器,接收端没有接收滤波器 ③信道是加性高斯白噪声信道 数字基带信号传输系统棋型如图1所示: 发送 接收 抽样 滤波器 滤波器 判决器 噪声 图1数字基带信号传输系统棋型 当P(1)=P(0)=1/2 时:最佳判决门限::=0,误码率: 2 故可用Q函数表示误码率P=Q(VF)。抽样判决器输入信噪比: r=A2/σ2抽样判决器输入信号为: rl=A+n,发1 0=-A+n2,发0 ±A为判决器输入有用信号电压,2,n,为信道输入的均值为0,方差为σ2高斯噪声。 通信系统的蒙特卡罗仿真模型如图2所示。编程实现二进制基带通信系统的误码率的蒙 特卡罗仿真,并和理论误码率比较。 16
Matlab 与通信仿真 16 为相对频率,定义为 N N A 。这样,在相对频率的意义下,事件 A 发生的概率可以通过重复 无限多次随机实验来求得,即: ( ) lim A N N P A → N = 在二进制数字通信系统中,若 N 是发送端发送的总码元数, NA 是差错发生的次数,则 总误码率可通过蒙特卡罗算法计算。 三、实验内容 1.产生随机数。 利用 rand 函数产生 5×4 的(0,2)内均匀分布的随机数; 利用 randn 函数产生 5×4 的均值为 0,方差为 2 的高斯分布的随机数。 2.利用随机数产生单极性基带信号,每一个码元要采 8 个样值,并画出其波形和功率谱密。 3.利用蒙特卡罗算法仿真二进制双极性基带通信系统的误码率。 假定通信系统满足以下条件: ① 信源输出的数据符号是相互独立和等概的双极性基带信号 ② 发送端没有发送滤波器,接收端没有接收滤波器 ③ 信道是加性高斯白噪声信道 数字基带信号传输系统模型如图 1 所示: 发送 滤波器 接收 滤波器 噪声 抽样 判决器 图 1 数字基带信号传输系统模型 当 P P (1 0 1 2 ) = = ( ) 时:最佳判决门限: 0 Vd = ,误码率: 1 A 1 2 2 2 2 e n r P erfc erfc = = ,利用 2 1 / 2 ( ) 2 t x Q x e dt − = , 2 2 ( ) t x erfc x e dt − = , 可得 1 ( ) ( ) 2 2 x Q x erfc = ,故可用 Q 函数表示误码率 ( ) P Q r e = 。抽样判决器输入信噪比: 2 2 A n r = 抽样判决器输入信号为: 1 2 1 A 1 0 A 0 r n r n = + = − + , 发 , 发 A 为判决器输入有用信号电压, 1 n , 2 n 为信道输入的均值为 0,方差为 2 n 高斯噪声。 通信系统的蒙特卡罗仿真模型如图 2 所示。编程实现二进制基带通信系统的误码率的蒙 特卡罗仿真,并和理论误码率比较
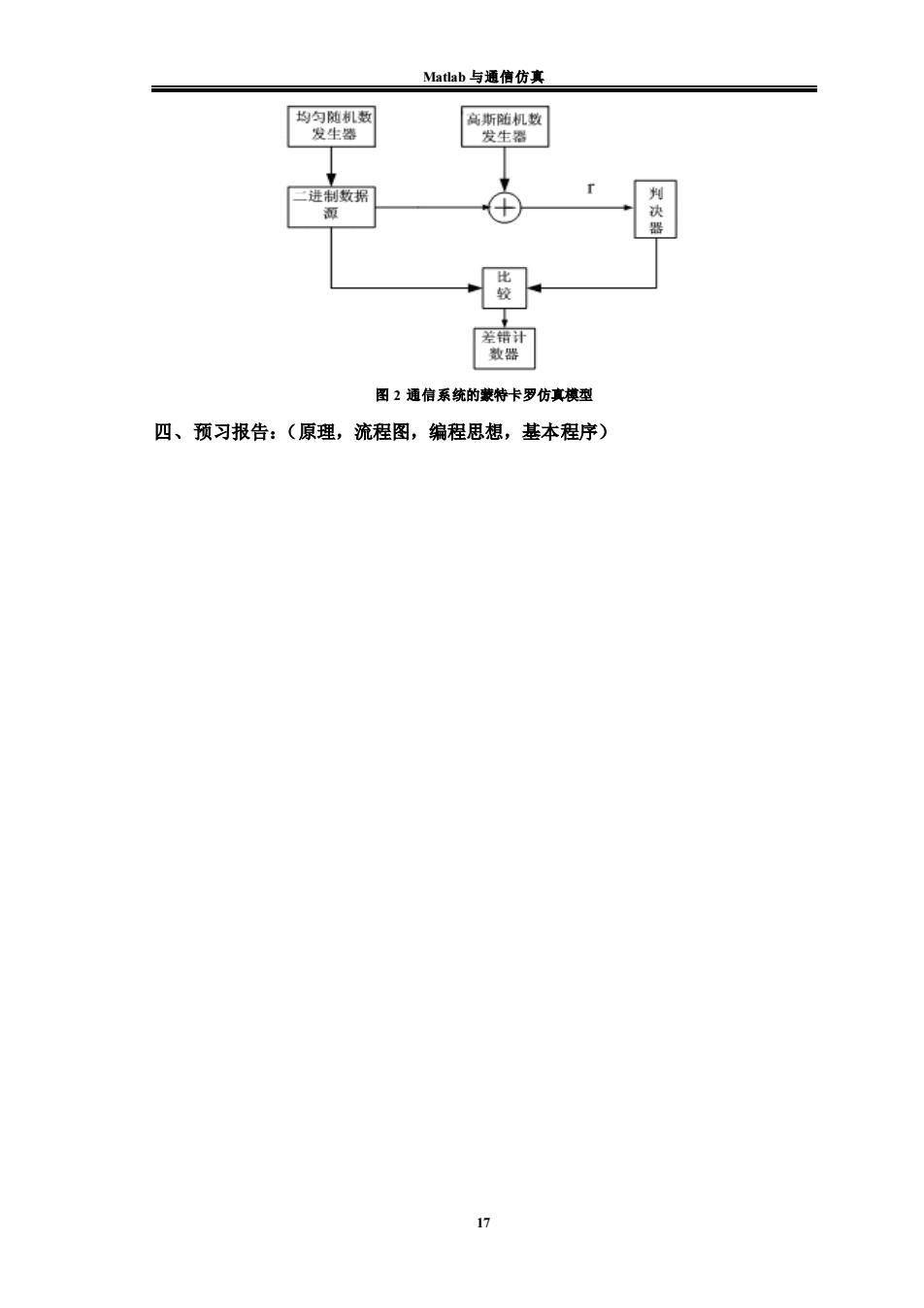
Matlab与通信仿真 均匀随机数 高斯随机数 发生鉴 发生器 进制数据 判 源 器 比 差错计 数器 图2通信系统的蒙特卡罗仿真模型 四、预习报告:(原理,流程图,编程思想,基本程序) 17
Matlab 与通信仿真 17 图 2 通信系统的蒙特卡罗仿真模型 四、预习报告:(原理,流程图,编程思想,基本程序)

Matlab与通信仿真 8
Matlab 与通信仿真 18