
2-1-3二元三点Lagrange插值简介一自学 正 二元函数Z=f(x,y)的插值 例:实际气体反应的经验平衡常数K,是温度T和压力的函 数,在给定的温度区间和压力区间内,求任意温度、压力下 的经验平衡常数K· K。=f(T,p) 基本思想: 先固定X对y做一元插值,然后固定y对X做一元插值。 二元函数的Lagrange插值公式: 功-客
二元函数Z=f(xi,y)的插值 例:实际气体反应的经验平衡常数Kp是温度T和压力p的函 数,在给定的温度区间和压力区间内,求任意温度、压力下 的经验平衡常数Kp。 2- 1- 3 二元三点Lagrange插值简介——自学 K f (T, p) p = 基本思想: 先固定x对y做一元插值,然后固定y对x做一元插值。 二元函数的Lagrange插值公式 : ∑ ∑ ∏ ∏ = = ≠ = ≠ = ⎥⎥⎥⎦⎤ ⎢⎢⎢⎣⎡ −− −− = ni mj i j ml i j ll nk i k i kk f x y y y y y x x x x f x y 1 1 1 1 ( , ) ( ) ( ) ( , )

2-1-4小结及注意事项 1.进行内插之前,先要对已知实验点进行误差分析,删除 一些明显不合理的结果。然后初步作出实验曲线图。观 察曲线变化规律以利于插值方法的选择或插值的分段。 2.如果精度要求不高,使用线性插值就可以了。 3.如果将Lagrange插值法使用得当是可以得到满意的插值 结果的。使用Lagrange插值法时,最好在需要插值点的 附近选取一些实验点,或按曲线变化情况选点。注意, 如选点过多有时会误差更大。这是高次多项式的插值所 造成的
2- 1- 4 小结及注意事项 1.进行内插之前,先要对已知实验点进行误差分析,删除 一些明显不合理的结果。然后初步作出实验曲线图。观 察曲线变化规律以利于插值方法的选择或插值的分段。 2.如果精度要求不高,使用线性插值就可以了。 3.如果将Lagrange插值法使用得当是可以得到满意的插值 结果的。使用Lagrange插值法时,最好在需要插值点的 附近选取一些实验点,或按曲线变化情况选点。注意, 如选点过多有时会误差更大。这是高次多项式的插值所 造成的
引言—变量之间的关系 ☑合D 理想气体:pV=nRT 函数关系 Arrhenius公式: k=AeE/RT 相关关系 回归分析法:寻找隐藏在随机性后面的 统计规律性。 解决: 1定量地研究变量之间的相关性; 2检验变量相关的显著性; 3.应用回归方程进行预测
引言——变量之间的关系 函数关系 相关关系 理想气体 : pV=nRT 回归分析法: 寻找隐藏在随机性后面的 统计规律性。 解决: 1.定量地研究变量之间的相关性; 2.检验变量相关的显著性; 3. 应用回归方程进行预测。 Arrhenius Arrhenius公式: Ea RT k Ae− =
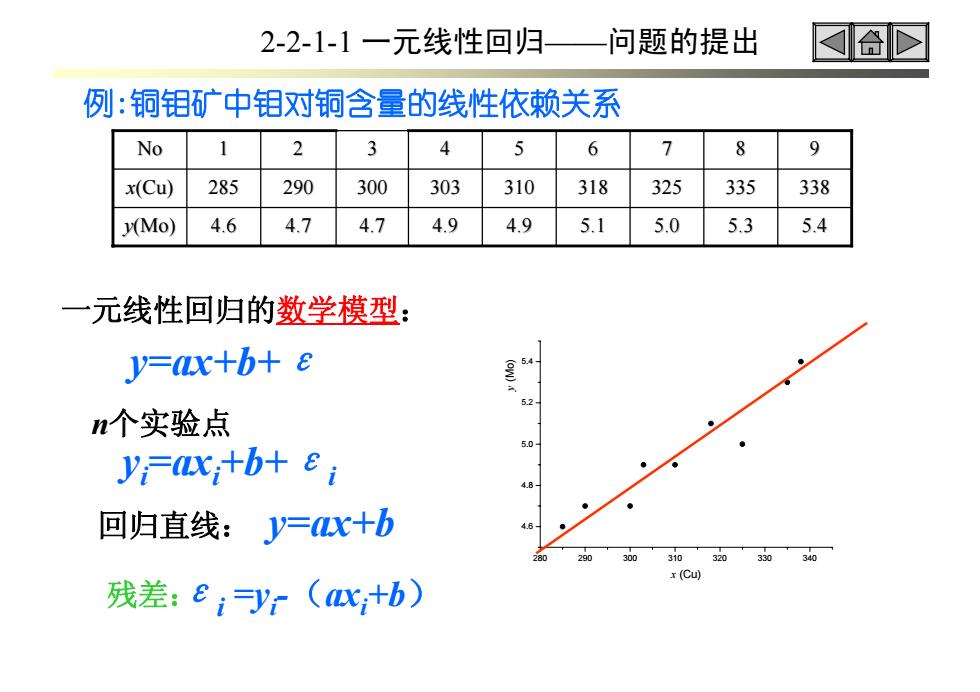
2-2-1-1一元线性回归 问题的提出 合D 例:铜钼矿中钼对铜含量的线性依赖关系 No 1 2 3 4 5 6 7 8 9 x(Cu) 285 290 300 303 310 318 325 335 338 y(Mo) 4.6 4.7 4.7 4.9 4.9 5.1 5.0 5.3 5.4 一元线性回归的数学模型: y=ax+b+8 n个实验点 yi=ax;+b+e; 回归直线:J=x+b 310 320 30 x(Cu) 残差:E;yr(心,+b)
2-2-1-1 一元线性回归——问题的提出 280 290 300 310 320 330 340 4.6 4.8 5.0 5.2 5.4 y (Mo) x (Cu) 例:铜钼矿中钼对铜含量的线性依赖关系 y(Mo) 4.6 4.7 4.7 4.9 4.9 5.1 5.0 5.3 5.4 x(Cu) 285 290 300 303 310 318 325 335 338 No 1 2 3 4 5 6 7 8 9 一元线性回归的数学模型: y=ax+b+ε yi=axi+b+εi n个实验点 回归直线: y=ax+b 残差:εi =yi-(axi+b)

2-2-1-2一元线性回归一方法原理 正 最小二乘法: 第i点残差: ei=y(ax;+b) 当残差的平方和为最小时,对应的α、b值是最佳值。 0-2-2y-a-y 0=-220y-a-bx)=0 am+b∑x=∑y i=l 0=-220y-a-bx)=0 a∑x+b∑x=∑xy ab (正规方程组) ∑y∑∑% ∑-∑x
最小二乘法: 第i点残差: εi =yi-(axi+b) 当残差的平方和为最小时,对应的a、b值是最佳值。 ∑ ∑ = = = = − − n i i i n i i Q y a bx 1 2 1 2 ε ( ) ∑ ∑ = = = − − − ⋅ = ∂ ∂ = − − − = ∂ ∂ n i i i i n i i i y a bx x bQ y a bx a Q 1 1 2 ( ) 0 2 ( ) 0 i i i i i i a x b x x y an b x y ∑ ∑ ∑ ∑ ∑ + = + = 2 2 2 ( ) 1 1 ∑ ∑ ∑ ∑ ∑ ∑ ∑ − − = − = i i i i i i i i x n x x y n x y b n y b x a (正规方程组) 2-2-1-2 一元线性回归——方法原理