2-1-1-2线性插值— 方法原理 线性插值原理: 两点间直线方程: y-yi-1_yi-yi- X-X-1 Xi-Xi-1 p,()=y=y+Y-(x-x) X-Xi-1 y=p(x) y y=fx) Xi-1 Xi
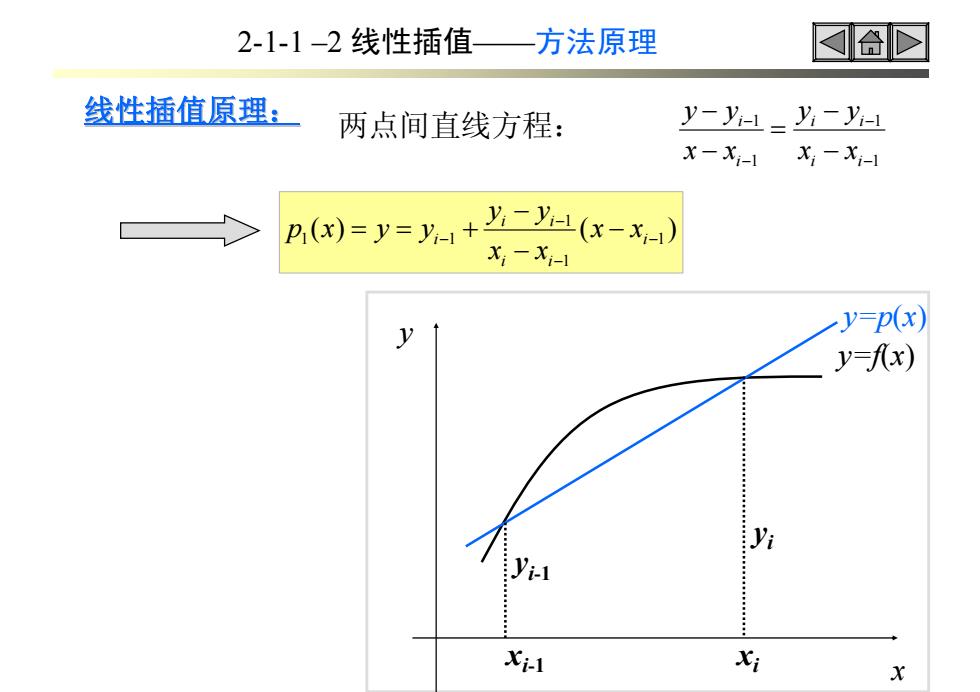
线性插值原理: 线性插值原理: 两点间直线方程: 1 1 1 1 − − − − − − = − − i i i i i i x x y y x x y y ( ) ( )1 1 1 1 1 − − − − − − − = = + i i i i i i x x x x y y p x y y x y y=f(x) y=p(x) xi-1 yi-1 xi yi 2-1-1 –2 线性插值——方法原理

2-1-1-2线性插值 方法原理 分段线性插值: 实验点个数为n时,求插值结点x的 函数值。首先确定x在哪两点间 x<x<CHI )=y+-04-y) XJ1-XJ J=1 x≤X2 i, X<X≤X+12 i=2,3,…,n-1 n-1,x>Xn-
分段线性插值: 分段线性插值: 实验点个数为n时,求插值结点 x的 函数值。首先确定x在哪两点间 xi<x<xi+1 1 1 2 1 1 1, , , 2,3, , 1 1, ( ) ( ) − + + + − > < ≤ = − = ≤ − − − = + n i i J J J J J J n x x i x x x i n J x x y y x x x x y x y L 2-1-1 –2 线性插值——方法原理
2-1-1-3线性插值 程序框图 ☑合 LINEPLOT(N.X.Y.XO,YO) DOJ=1,N-1> J1=J+1 yes X0<=X(J1) no CONTINUE J=J-1 T=(X0-X(J)/(x(J1)-x(J) YO=Y(J)+T*(Y(J1)-Y(J)) RETURN
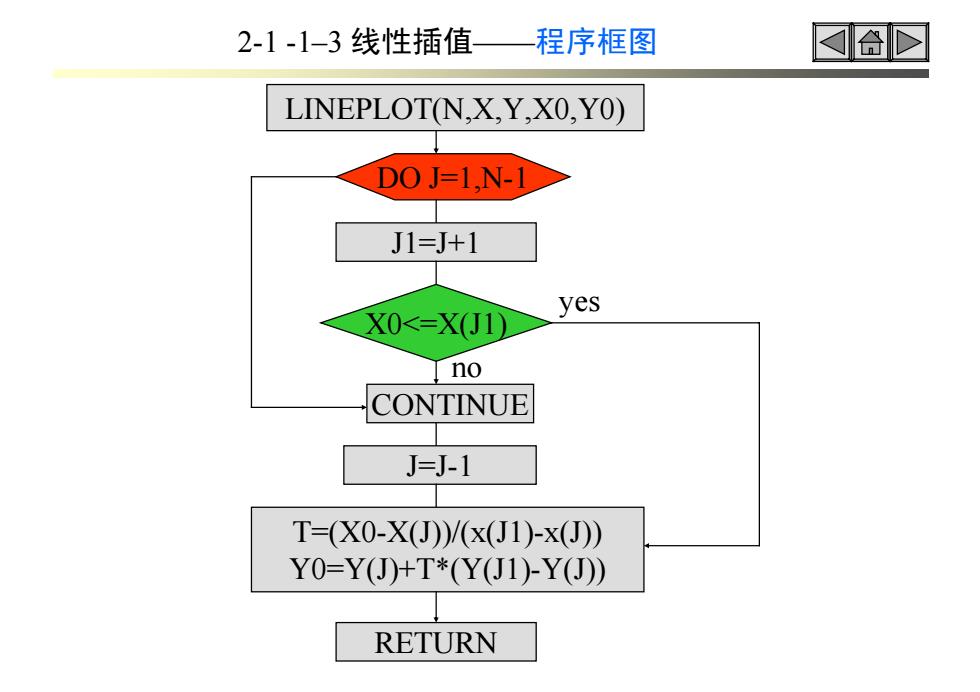
LINEPLOT(N,X,Y,X0,Y0) DO J=1,N-1 J1=J+1 X0<=X(J1) CONTINUE J=J-1 T=(X0-X(J))/(x(J1)-x(J)) Y0=Y(J)+T*(Y(J1)-Y(J)) RETURN no yes 2-1 -1–3 线性插值——程序框图
2-1-1-4线性插值 应用示例 合D 开始 输入:数据点X①,Y(①,未知点X0 调用线性插值子程序求未知点X0对应的函数值Y0 输出:X0,Y0值 结束 显示程序 显示输入 显示输出 合
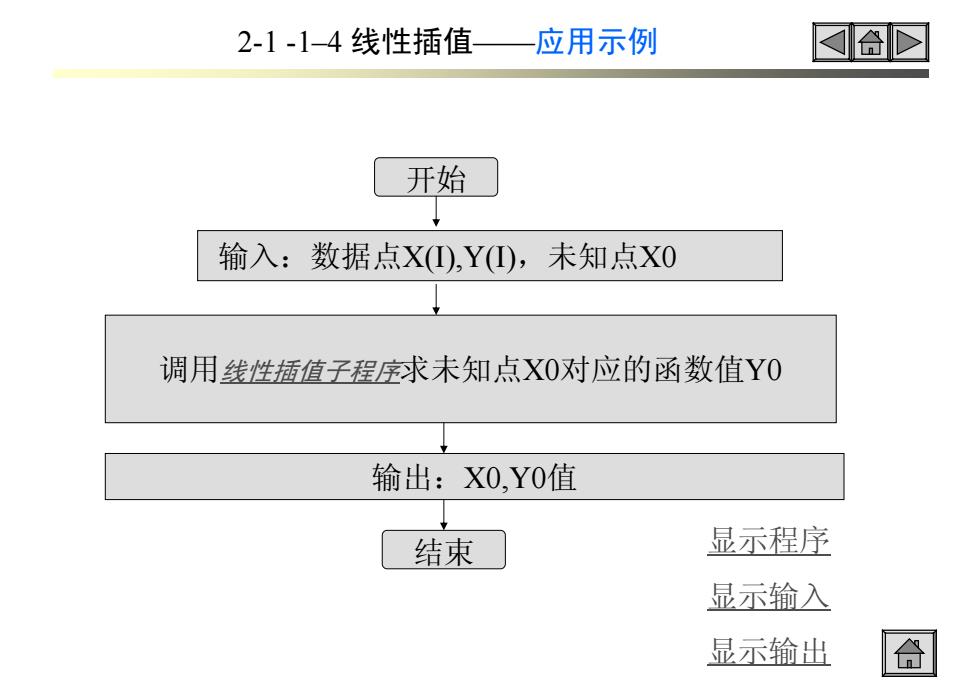
开始 输入:数据点X(I),Y(I),未知点X0 调用线性插值子程序求未知点X0对应的函数值Y0 输出:X0,Y0值 结束 2-1 -1–4 线性插值——应用示例 显示程序 显示输入 显示输出
2-1-2-1一元三点Lagrange插值 问题的提出 合D 例:计算乙醇的平均摩尔体积 实验测得25℃时乙醇溶液的平均摩尔体积,(cmmo1)与乙 醇的物质的量分数的关系如下 x m /cm2mol1 计算x=0.1,0.2,0.3,0.4 0.0891 21.22 时的Vm。 0.1153 22.16 0.1435 23.18 0.1739 24.32 0.2068 25.57 0.2424 26.95 0.2811 28.47 0.3234 30.15 0.3697 32.01 0.4207 34.07 0.4771 36.37
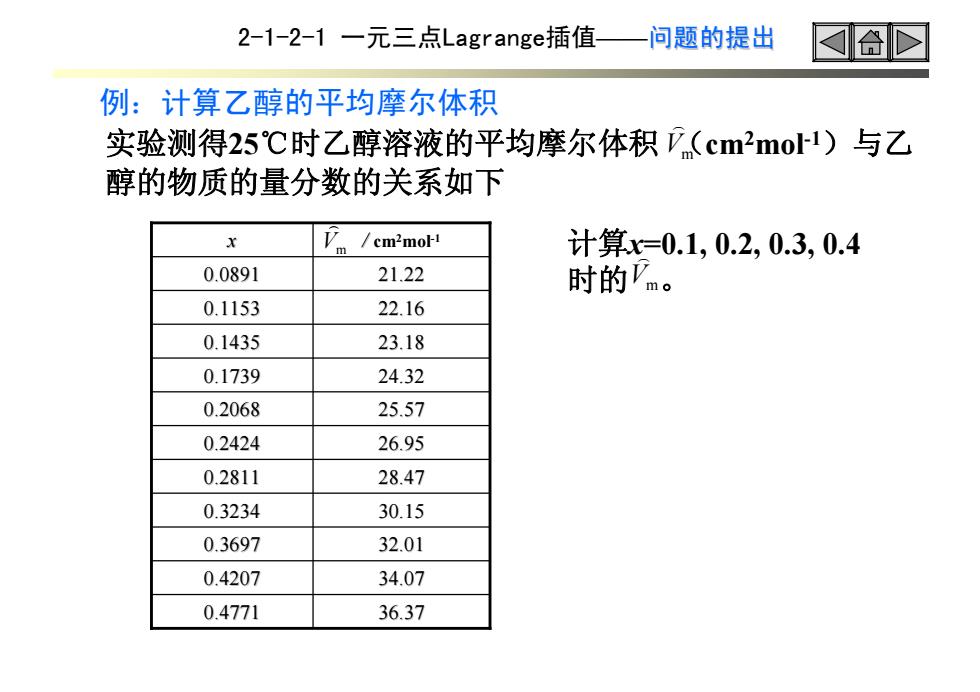
2-1-2-1 一元三点Lagrange插值——问题的提出 例:计算乙醇的平均摩尔体积 实验测得25℃时乙醇溶液的平均摩尔体积 (cm 2mol-1)与乙 醇的物质的量分数的关系如下 0.4771 36.37 0.4207 34.07 0.3697 32.01 0.3234 30.15 0.2811 28.47 0.2424 26.95 0.2068 25.57 0.1739 24.32 0.1435 23.18 0.1153 22.16 0.0891 21.22 / cm2mol-1 x 计算x=0.1, 0.2, 0.3, 0.4 时的 。 Vm ) Vm ) Vm )