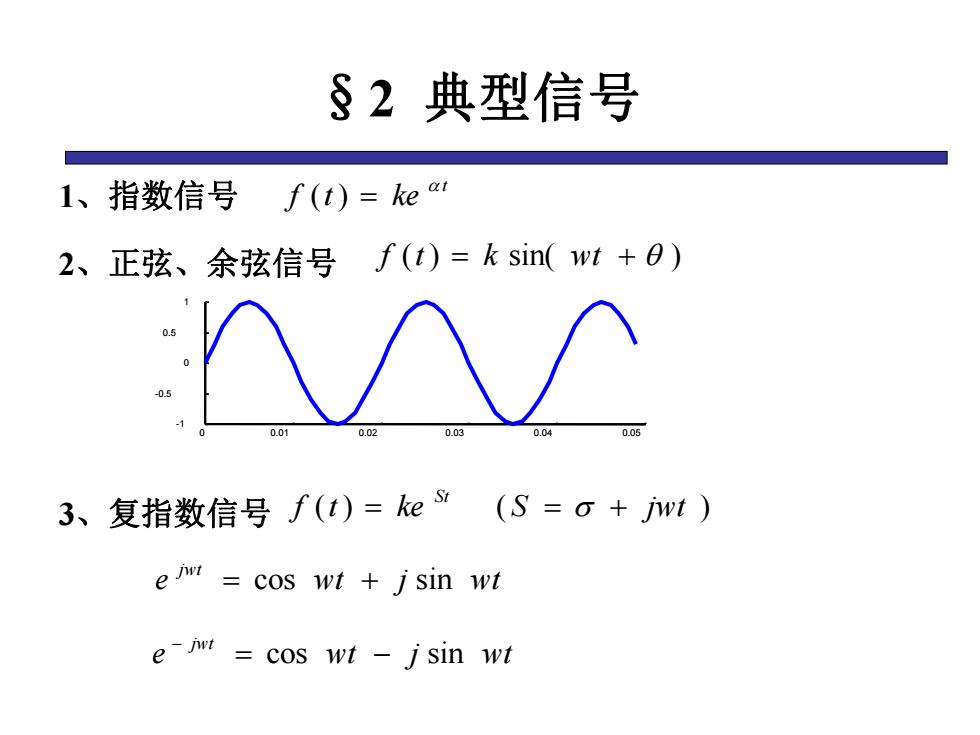
§2典型信号 1、 指数信号f(t)=ke 2、正弦、余弦信号 f(t)=k sin(wt +0) 3、 复指数信号f(t)=和” (S=o+jwt em cos wt +j sin wt e-m cos wt -j sin wt
§2 典型信号 1、指数信号 2、正弦、余弦信号 3、复指数信号 t f t ke ( ) f (t) k sin( wt ) 0 0.01 0.02 0.03 0.04 0.05 -1 -0.5 0 0.5 1 f (t) ke ( S jwt ) St e wt j wt jwt cos sin e wt j wt jwt cos sin
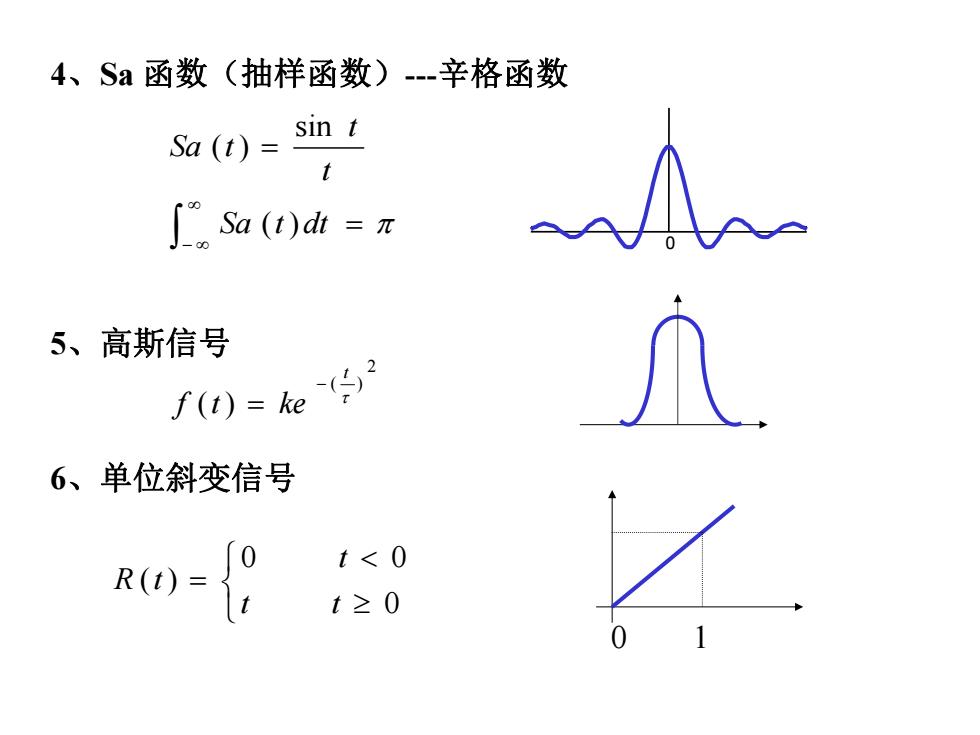
4、Sa函数(抽样函数)-辛格函数 sin t Sa(t)= ∫sa()dh=π 5、高斯信号 f(t)=ke 6、单位斜变信号 t<0 R(t) t≥0
0 4、Sa 函数(抽样函数)-辛格函数 5、高斯信号 6、单位斜变信号 Sa t dt t t Sa t ( ) sin ( ) 2 ( ) ( ) t f t ke 0 1 0 0 0 ( ) t t t R t
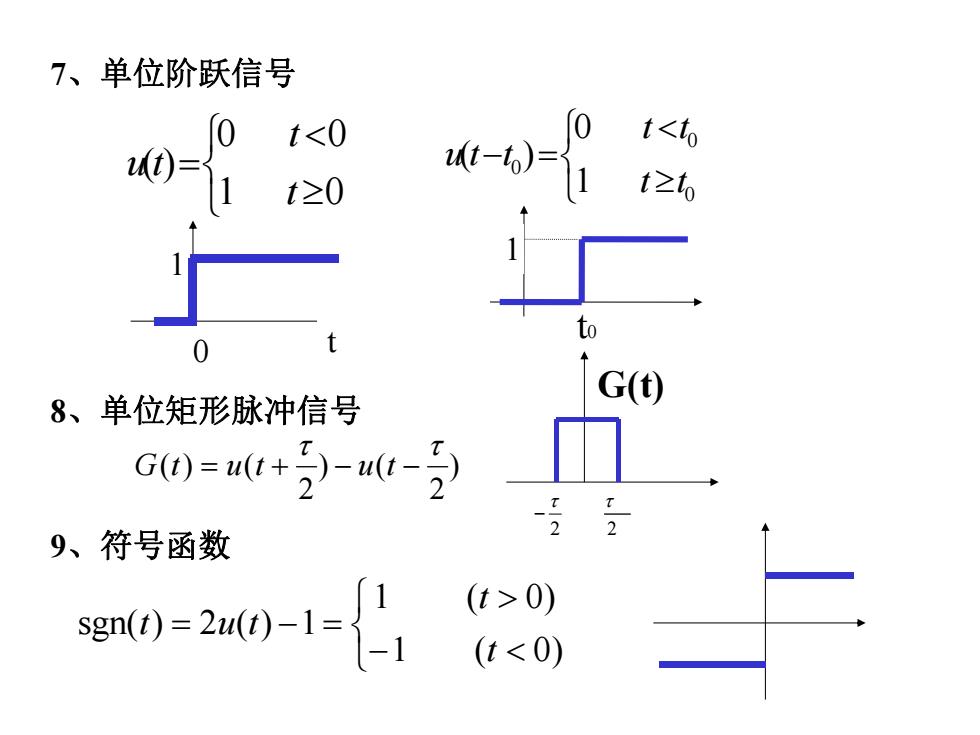
7、单位阶跃信号 t-6) 0 t<t G() 8、单位矩形脉冲信号 G0=+-1-7 9、符号函数 80-2a0-1 (t>0) (t<0)
7、单位阶跃信号 8、单位矩形脉冲信号 9、符号函数 0 0 0 1 0 ( ) t t t t u t t 1 0 0 0 ( ) t t u t t0 1 1 t 0 ) 2 ) ( 2 ( ) ( G t u t u t G(t) 2 2 1 ( 0) 1 ( 0) sgn( ) 2 ( ) 1 t t t u t
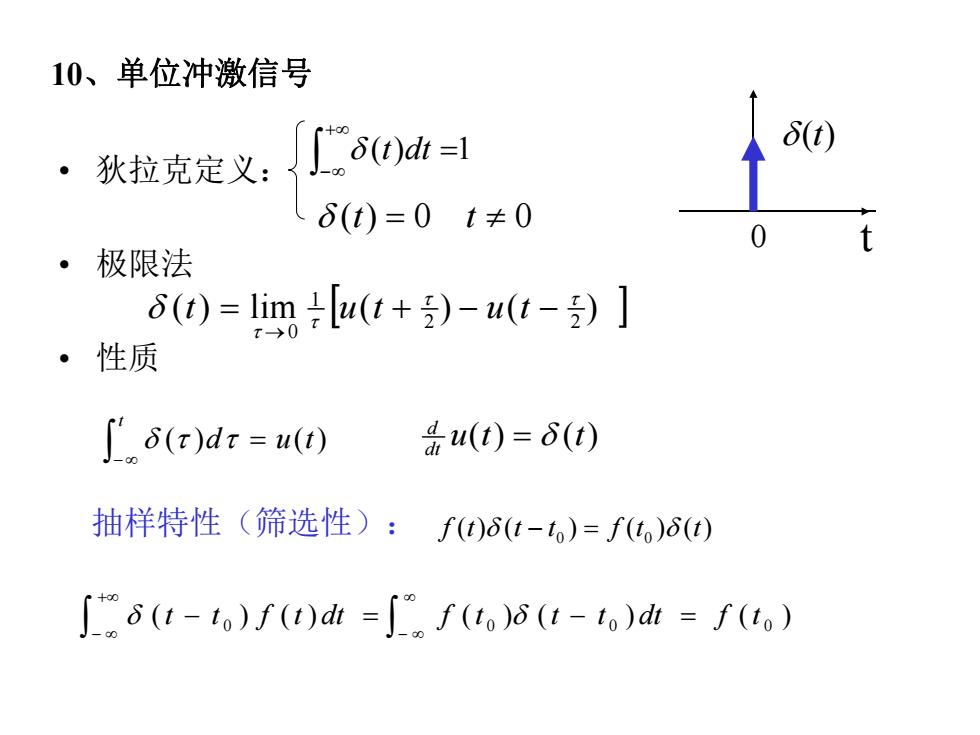
10、单位冲激信号 狄拉克定义: 6o)h=1 (6(t)=0t≠0 0 1 。极限法 (0=limu(t+)-u(t-)] 。性质 ∫'6(x)dr=u(t) 4(t)=δ(t) 抽样特性(筛选性):ft)6(t-to)=ft,)δ() δ(t-to)f(u)dk=f(to)δ(t-to)d=f(o)
10、单位冲激信号 • 狄拉克定义: • 极限法 • 性质 ( ) 1 t dt (t) 0 t (t) 0 t 0 ( ) lim ( ) ( ) 2 2 1 0 t u t u t t ( )d u(t) ( ) ( ) ( ) ( ) ( ) 0 0 0 0 t t f t dt f t t t dt f t u(t) (t) dt d 抽样特性(筛选性): ( ) ( ) ( ) ( ) 0 0 f t t t f t t
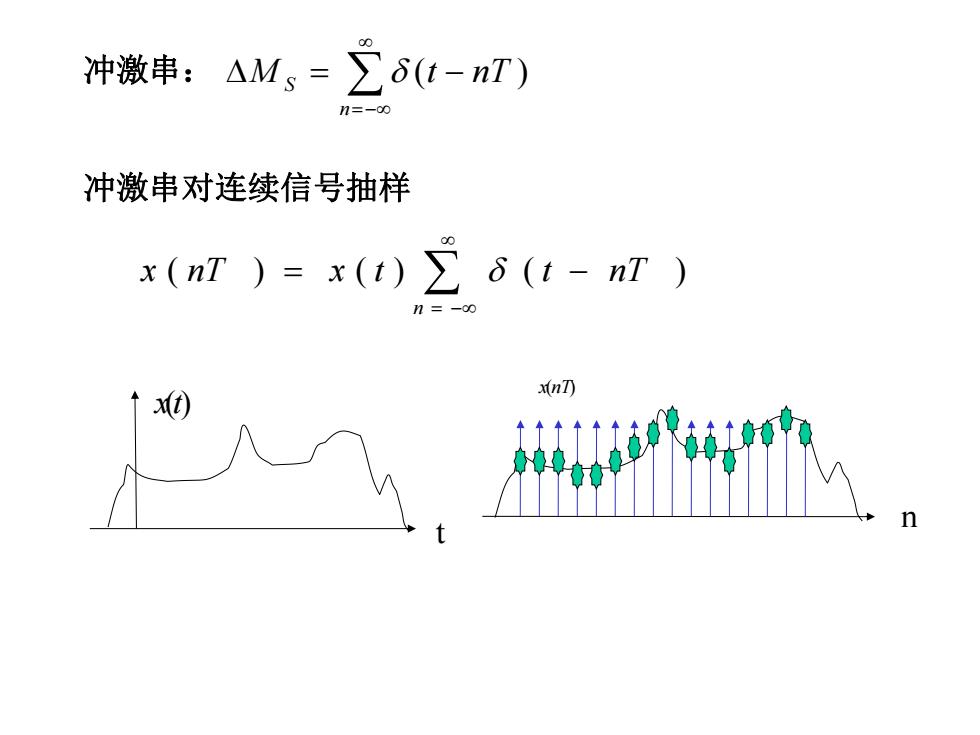
冲激串:△M,=∑6(t-nT) 冲激串对连续信号抽样 x(n)=x(t)∑6(t-n) x(nT)
冲激串: 冲激串对连续信号抽样 n x ( nT ) x ( t ) ( t nT ) x(t) t x(nT) n n M S (t nT )