
■子 分子振动必须伴随偶极矩的变化,只有发 生偶极矩变化(△u≠0)的振动才能引起可 观测的红外吸收光谱,该分子称为红外活 性的。△u=0的分子振动不能产生红外振动 吸收,称为非红外活性的。 Create PDF files without this message by purchasing novaPDF printer(http://www.novapdf.com)
分子振动必须伴随偶极矩的变化,只有发 生偶极矩变化(0)的振动才能引起可 观测的红外吸收光谱,该分子称为红外活 性的。=0的分子振动不能产生红外振动 吸收,称为非红外活性的。 Create PDF files without this message by purchasing novaPDF printer (http://www.novapdf.com)
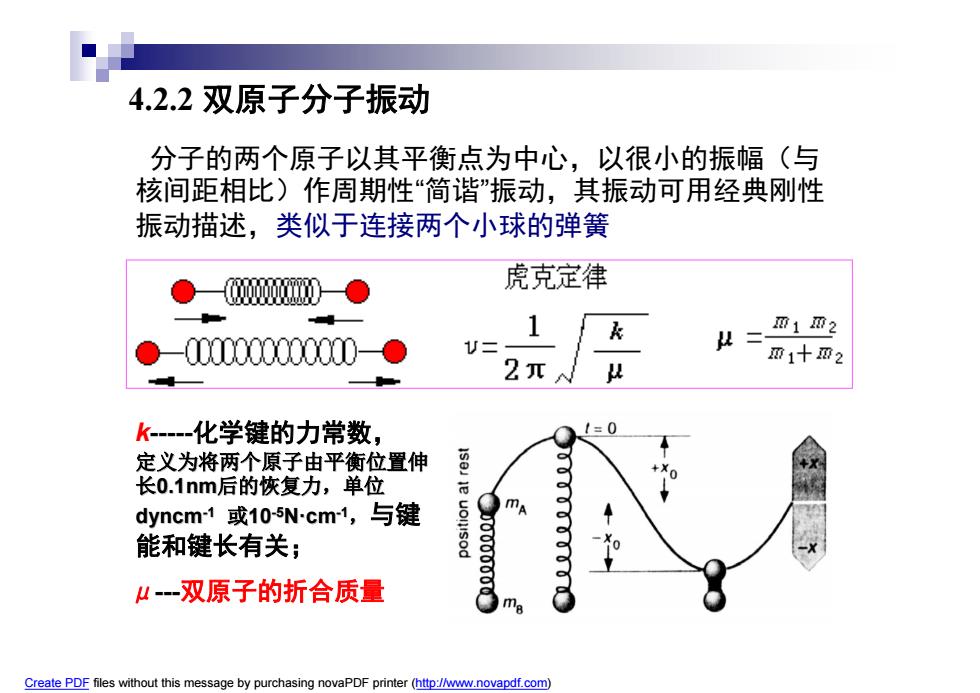
4.2.2双原子分子振动 分子的两个原子以其平衡点为中心,以很小的振幅(与 核间距相比)作周期性“简谐”振动,其振动可用经典刚性 振动描述,类似于连接两个小球的弹簧 虎克定律 1 m102 D-00000000000004 2π m1十亚2 k-一化学键的力常数, 1=0 定义为将两个原子由平衡位置伸 长0.1nm后的恢复力,单位 dyncm1或10-5Ncm1,与键 能和键长有关; 4一双原子的折合质量 Create PDF files without this message by purchasing novaPDF printer(http://www.novapdf.com)
k-化学键的力常数, 定义为将两个原子由平衡位置伸 长0.1nm后的恢复力,单位 dyncm-1 或10-5N·cm-1 ,与键 能和键长有关; μ-双原子的折合质量 4.2.2 双原子分子振动 分子的两个原子以其平衡点为中心,以很小的振幅(与 核间距相比)作周期性“简谐”振动,其振动可用经典刚性 振动描述,类似于连接两个小球的弹簧 Create PDF files without this message by purchasing novaPDF printer (http://www.novapdf.com)

双原子分子振动频率: 或用波数表示: 2πc 如折合质量u以原子质量为单位;k以N/Cm为单位。 则有: =1303 -em-1) 2πC A.IN A 其中:1303=(2cN4×1055N4=6022×102 mol -1) A.三 A,)A,(2) A,)+A,(2) 可见分子的振动频率与化学键的力常数、原子质量有关。 Create PDF files without this message by purchasing novaPDF printer(http://www.novapdf.com)
2 c 1 ( ) ~ 可见分子的振动频率与化学键的力常数、原子质量有关。 或用波数表示: 如折合质量 以原子质量为单位;k以N/cm为单位。 则有: u k 2π 1 双原子分子振动频率: (cm ) ' r A k A /N ' r A k πc ν 1 1303 2 1 . mol ) A ) N A N πc 其中: ( 23 1 ; 6 022 10 5 10 2 1 1303 (1 ) ( 2 ) ' ( 1 ) ( 2 ) r r r r r A A A A A Create PDF files without this message by purchasing novaPDF printer (http://www.novapdf.com)
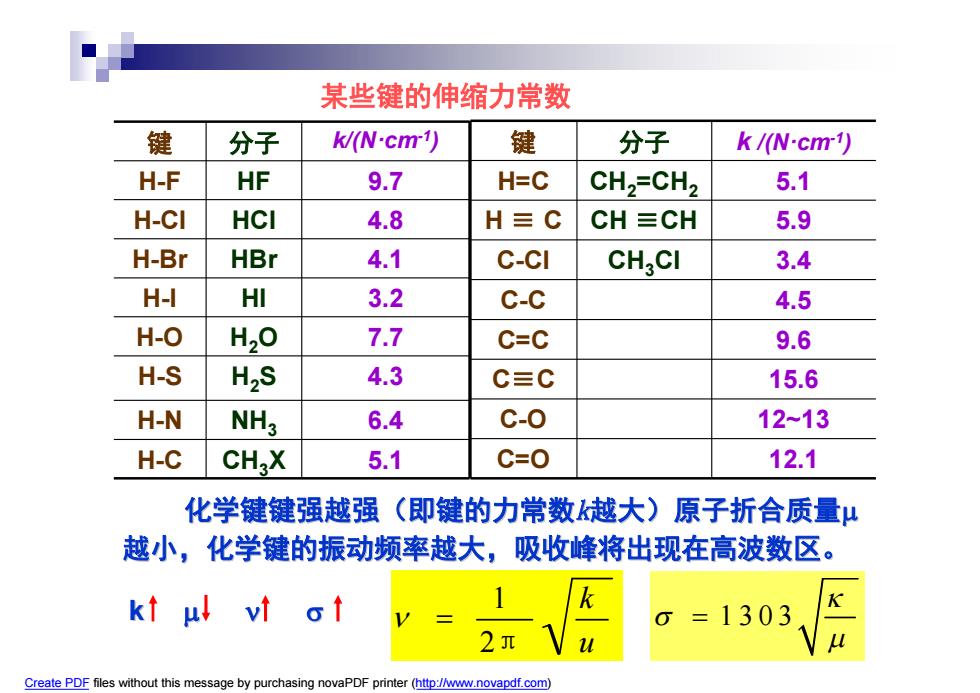
某些键的伸缩力常数 键 分子 kWN·cm) 键 分子 k/(N-cm1) H-F HF 9.7 H=C CH2=CH2 5.1 H-CI HCI 4.8 H≡C CH≡CH 5.9 H-Br HBr 4.1 C-CI CHCI 3.4 HI HI 3.2 C-C 4.5 H-O H,O 7.7 C=C 9.6 H-S H2S 4.3 C≡C 15.6 H-N NH3 6.4 C-0 12~13 H-C CH2X 5.1 C=O 12.1 化学键键强越强(即键的力常数越大)原子折合质量μ 越小,化学键的振动频率越大,吸收峰将出现在高波数区。 kt ul vt ot =1303 2元 Create PDF files without this message by purchasing novaPDF printer(http://www.novapdf.com)
某些键的伸缩力常数 H-C CH3X 5.1 H-N NH3 6.4 H-S H2S 4.3 H-O H2O 7.7 H-I HI 3.2 H-Br HBr 4.1 H-Cl HCl 4.8 H-F HF 9.7 k/(N·cm-1 键 分子 ) 化学键键强越强(即键的力常数k越大)原子折合质量 越小,化学键的振动频率越大 化学键的振动频率越大,吸收峰将出现在高波数区 吸收峰将出现在高波数区。 C=O 12.1 C-O 12~13 C≡C 15.6 C=C 9.6 C-C 4.5 C-Cl CH3Cl 3.4 H ≡ C CH ≡CH 5.9 H=C CH2=CH2 5.1 k /(N·cm-1 键 分子 ) k u k 2π 1 1 3 0 3 Create PDF files without this message by purchasing novaPDF printer (http://www.novapdf.com)

例1:由表中查知C-C键的e9.6(N/cm),计算 正己烯中C=C键伸缩振动频率。实测值为1652 cm-1 0.6 o(cm)=1303 =1303 =1648.2 10 例2:由表中查知H-C1键的k=4.8(N/cm),计算 H-C1键伸缩振动频率。实测值为2885.9cm-1 1.008×35.45 4= =0.98 c(cm)=1303 =1303 4.8 2883.7 1.008+35.45 0.98 Create PDF files without this message by purchasing novaPDF printer(http://www.novapdf.com)
例1: 由表中查知 C=C 键的 k= 9.6 (N/cm) , 计算 正己烯中C=C键伸缩振动频率。实测值为1652 cm-1 -1 9.6 (cm ) 1303 1303 1648.2 12 2 k 例2: 由表中查知 H-Cl 键的k = 4.8 (N/cm),计算 H-Cl键伸缩振动频率。实测值为2885.9cm-1 -1 4.8 (cm ) 1303 1303 2883.7 0.98 k 1.008 35.45 0.98 1.008 35.45 Create PDF files without this message by purchasing novaPDF printer (http://www.novapdf.com)