
§12.2过渡态理论 过渡状态理论又称活化络合物理论,是1935年由艾林(E.Eyring),埃文斯(Evans)和 波兰尼(Polany)等人在统计热力学和量子力学的基础上提出来的。 该理论的重要性在于:可根据反应物分子的某些性质,如分子的大小、质量、振动频 率等求出反应速率常数,对定性认识化学反应提供了一个理论框架.因此,该理论也称 为绝对反应速率理论。 理论的基本思想 ()反应物分子发生有效碰撞是反应的前提条件,但不只是简单碰撞就变成产物,而 是反应物分子要经过以一定的构型存在的一个中间过渡态,又称活化络合物。形成这个活 化过渡态必须吸收一定的活化能,具有相对较高的能量而很不稳定,一方面很快与反应物 建立热力学平衡,另一方面又极易分解为产物,即两个具有足够能量的反应物分子相互接 近时,分子的价键要经过重排,能量经过重新分配,方能变成产物分子。这个过渡态就称为 活化络合物,所以又称为活化络合物理论。 A+B-C=X[A…B.CK,→A-B+C (2)活化络合物具有内部结构和各种运动形式,即平动,转动和振动等。但其中有一 个振动运动与其他振动不同,该振动无回复力,振动发生后活化体将分解为产物。活化物 与反应物分子间建立快化学平衡,总反应速度由活化络合物转化成产物的速度决定。 (3)反应物分子和活化络合物的能量分布均服从麦克斯韦尔玻兹曼分布。即反应物分 子间相互作用的势能是分子间相对位置的函数,由反应物变成产物过程中,体系的势能不 断变化。Ep=Ep(r) 利用该理论,只要知道分子的振动频率、质量、核间距等基本物性,就能计算反应的 速率系数,所以又称为绝对反应速率理论(absolute rate theory)。 一、过渡态理论的物理模型一势能面 化学反应是分子或原子之间的价电子的重排作用,表现为分子之间化学键的短裂和性 键的生成要了解化学作用的动力学实质(如活化能),就必须获得分子间化学相互作用。 该理论认为反应物分子间相互作用的势能是分子间相对位置的函数,Ep=Ep(r),对 于双原子体系,只有一个核间距,故可以表现在一个平面图上。 莫尔斯Morse)公式是对双原子分子最常用的计算势能Ep的经验公式: E.(r)=D.[exp{-2ar-)}-2exp{-a(r-)}] 式中~是分子中双原子分子间的平衡核间距 E De是势能曲线的井深 a为与分子结构有关的常数。 AB双原子分子根据该公式画出的势能曲线 D 如图所示。 这个势能曲线是一个键解离的曲线,由AB 双原子分子的莫尔斯势施曲线 分子的平衡核间距o(曲线最低点)向r增大方 向的一段曲线表示AB分子的解离,一般把原子 图12.4双原子分子的Morse势能面曲线 A和B处于无限远时(孤立原子)的势能取为零。体系的势能在平衡核间距0有最低点。 当>时,有引力,即化学键力;当<心时,有斥力。一般给出的是电子基态的势能曲
§12.2 过渡态理论 过渡状态理论又称活化络合物理论, 是 1935 年由艾林(E.Eyring),埃文斯(Evans)和 波兰尼(Polany)等人在统计热力学和量子力学的基础上提出来的。 该理论的重要性在于: 可根据反应物分子的某些性质, 如分子的大小、质量、振动频 率等求出反应速率常数, 对定性认识化学反应提供了一个理论框架. 因此, 该理论也称 为绝对反应速率理论。 理论的基本思想: (1) 反应物分子发生有效碰撞是反应的前提条件,但不只是简单碰撞就变成产物,而 是反应物分子要经过以一定的构型存在的一个中间过渡态,又称活化络合物。形成这个活 化过渡态必须吸收一定的活化能,具有相对较高的能量而很不稳定,一方面很快与反应物 建立热力学平衡,另一方面又极易分解为产物,即两个具有足够能量的反应物分子相互接 近时,分子的价键要经过重排,能量经过重新分配,方能变成产物分子。这个过渡态就称为 活化络合物,所以又称为活化络合物理论。 c r K K A B C X [A B C] A B C + − ⎯⎯→ − + (2) 活化络合物具有内部结构和各种运动形式,即平动,转动和振动等。但其中有一 个振动运动与其他振动不同,该振动无回复力,振动发生后活化体将分解为产物。活化物 与反应物分子间建立快化学平衡,总反应速度由活化络合物转化成产物的速度决定。 (3) 反应物分子和活化络合物的能量分布均服从麦克斯韦尔-玻兹曼分布。即反应物分 子间相互作用的势能是分子间相对位置的函数,由反应物变成产物过程中,体系的势能不 断变化。 Ep = Ep(r) 利用该理论,只要知道分子的振动频率、质量、核间距等基本物性,就能计算反应的 速率系数,所以又称为绝对反应速率理论(absolute rate theory)。 一、过渡态理论的物理模型—势能面 化学反应是分子或原子之间的价电子的重排作用,表现为分子之间化学键的短裂和性 键的生成.要了解化学作用的动力学实质(如活化能),就必须获得分子间化学相互作用。 该理论认为反应物分子间相互作用的势能是分子间相对位置的函数,Ep = Ep(r),对 于双原子体系,只有一个核间距,故可以表现在一个平面图上。 莫尔斯(Morse)公式是对双原子分子最常用的计算势能 Ep 的经验公式: p e 0 0 E r D a r r a r r ( ) [exp{ 2 ( )} 2exp{ ( )}] = − − − − − 式中 r0是分子中双原子分子间的平衡核间距 De 是势能曲线的井深 a 为与分子结构有关的常数。 AB 双原子分子根据该公式画出的势能曲线 如图所示。 这个势能曲线是一个键解离的曲线,由 AB 分子的平衡核间距 r0(曲线最低点)向 r 增大方 向的一段曲线表示 AB 分子的解离,一般把原子 A 和 B 处于无限远时(孤立原子)的势能取为零。体系的势能在平衡核间距 r0 有最低点。 当 r>r0 时,有引力,即化学键力;当 r<r0 时,有斥力。一般给出的是电子基态的势能曲 图 12.4 双原子分子的 Morse 势能面曲线
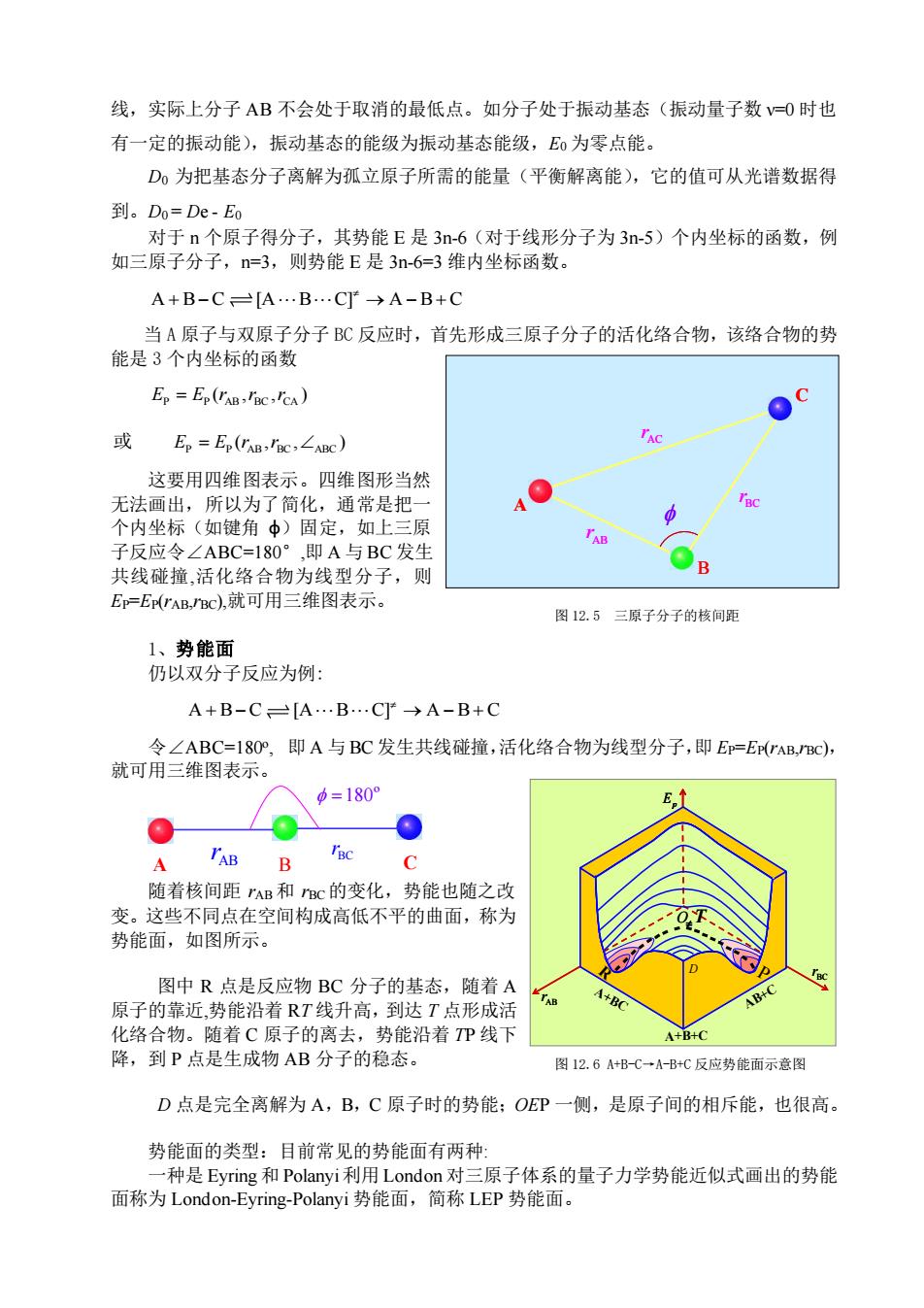
线,实际上分子AB不会处于取消的最低点。如分子处于振动基态(振动量子数v=0时也 有一定的振动能),振动基态的能级为振动基态能级,Eo为零点能。 D0为把基态分子离解为孤立原子所需的能量(平衡解离能),它的值可从光谱数据得 到。Do=De-Eo 对于n个原子得分子,其势能E是3n-6(对于线形分子为3n-5)个内坐标的函数,例 如三原子分子,n=3,则势能E是3n-6=3维内坐标函数。 A+B-C=[A…B…C]→A-B+C 当A原子与双原子分子BC反应时,首先形成三原子分子的活化络合物,该络合物的势 能是3个内坐标的函数 Ep Ep(TAB,VC,ICA) 或 Ep=Ep(IAB,'BC,∠ABC) 这要用四维图表示。四维图形当然 无法画出,所以为了简化,通常是把一 个内坐标(如键角中)固定,如上三原 子反应令∠ABC=180°,即A与BC发生 共线碰撞,活化络合物为线型分子,则 Ep=Er(rAB,BC),就可用三维图表示。 图12.5三原子分子的核间距 1、势能面 仍以双分子反应为例: A+B-C=[A…B.C]→A-B+C 令∠ABC=18O°,即A与BC发生共线碰撞,活化络合物为线型分子,即Ep=E(rAB,BC): 就可用三维图表示。 =180° E A B 随着核间距”AB和BC的变化,势能也随之改 变。这些不同点在空间构成高低不平的曲面,称为 势能面,如图所示。 BC 图中R点是反应物BC分子的基态,随着A 原子的靠近,势能沿着RT线升高,到达T点形成活 A+BC AB+C 化络合物。随着C原子的离去,势能沿着P线下 A+B+C 降,到P点是生成物AB分子的稳态。 图12.6A+B-C→A-B+C反应势能面示意图 D点是完全离解为A,B,C原子时的势能;OEP一侧,是原子间的相斥能,也很高。 势能面的类型:目前常见的势能面有两种 一种是Eyring和Polanyi利用London对三原子体系的量子力学势能近似式画出的势能 面称为London-Eyring-Polanyi势能面,简称LEP势能面
线,实际上分子 AB 不会处于取消的最低点。如分子处于振动基态(振动量子数 ν=0 时也 有一定的振动能),振动基态的能级为振动基态能级,E0 为零点能。 D0 为把基态分子离解为孤立原子所需的能量(平衡解离能),它的值可从光谱数据得 到。D0 = De - E0 对于 n 个原子得分子,其势能 E 是 3n-6(对于线形分子为 3n-5)个内坐标的函数,例 如三原子分子,n=3,则势能 E 是 3n-6=3 维内坐标函数。 A B C [A B C] A B C + − → − + 当 A 原子与双原子分子 BC 反应时,首先形成三原子分子的活化络合物,该络合物的势 能是 3 个内坐标的函数 P P AB BC CA E E r r r = ( , , ) P P AB BC ABC 或 ( , , ) E E r r = 这要用四维图表示。四维图形当然 无法画出,所以为了简化,通常是把一 个内坐标(如键角 φ)固定,如上三原 子反应令∠ABC=180°,即 A 与 BC 发生 共线碰撞,活化络合物为线型分子,则 EP=EP(rAB,rBC),就可用三维图表示。 1、势能面 仍以双分子反应为例: A B C [A B C] A B C + − → − + 令∠ABC=180o , 即 A 与 BC 发生共线碰撞,活化络合物为线型分子,即 EP=EP(rAB,rBC), 就可用三维图表示。 A AB B C r BC r =180º 随着核间距 rAB 和 rBC 的变化,势能也随之改 变。这些不同点在空间构成高低不平的曲面,称为 势能面,如图所示。 图中 R 点是反应物 BC 分子的基态,随着 A 原子的靠近,势能沿着 RT 线升高,到达 T 点形成活 化络合物。随着 C 原子的离去,势能沿着 TP 线下 降,到 P 点是生成物 AB 分子的稳态。 D 点是完全离解为 A,B,C 原子时的势能;OEP 一侧,是原子间的相斥能,也很高。 势能面的类型:目前常见的势能面有两种: 一种是 Eyring 和 Polanyi利用 London 对三原子体系的量子力学势能近似式画出的势能 面称为 London-Eyring-Polanyi 势能面,简称 LEP 势能面。 图 12.5 三原子分子的核间距 AB r AC r A B C BC r 图 12.6 A+B-C→A-B+C 反应势能面示意图 BC r AB r Ep O Ep O A+BC AB+C A+B+C R D P T

另一种是Sato又在这个基础上进行了修正,使势垒顶端不合理的势阱消失,这样得到 的势能面称为London-Eyring-Polanyi-Sato势能面,简称LEPS势能面。 如何获得势能面(意义和用途) 对于一个基元反应,如果能准确地获得势能面,就能知道它过渡态的势能大小,从势 能面上推测最可能的反应途径,从过渡态势能面的位置可确定活化能,这将给出重要的反 应动力学信息。因此如何获得势能面就成为化学动力学的重要任务,不过,目前只能对简 单的基元反应得到准确的势能面。研究最多的是H+H2和F+H2反应。 获得势能面的方法有三种: (1)纯理论方法通过量子力学计算。每个原子和分子有薛定谔方程,然后用量子 力学求解得到势能面。 (2)半经验方法也源于量子力学,但它应用了经验的双原子分子的势能公式 -Morse:E (r)=D.[exp{-2a(r-o);-2exp{-a(r-r)] (3)纯经验方法:如Mors势能公式或其它经验公式。 2、马鞍点(saddle point) 在势能面上,活化络合物所处的位置T点称为马鞍点。 该点势能与反应物和生成物所处的稳定态能量R点和P点 相比是最高点,但与坐标原点一侧和D点的势能相比又是最低 点 如把势能面比作马鞍的话,则马鞍点处在马鞍的中心。从 反应物到生成物必须越过一个能垒。 马鞍形 3、反应坐标reaction coordinate)势能面 反应坐标是一个连续变化的参数,其每一个值 势 都对应于沿反应体系中各原子的相对位置。如在势 …B…C] 能面上,反应沿着RT→TP的虚线进行,反应进程 不同,各原子间相对位置也不同,体系的能量也不 AB+C 同。 如以势能为纵坐标,反应坐标为横坐标,画出 A+BC 的图可以表示反应过程中体系势能的变化,这是一 反应坐标 条能量最低的途径。 势能割面图 沿势能面上R-TP虚线切剖面图,把R-TP曲 线作横坐标,这就是反应坐标。以势能作纵坐标,标出反应进程中每一点的势能,就得到 势能面的剖面图。 从反应物A+BC到生成物走的是能量 最低通道,但必须越过势能垒Eb,Eb是 70 活化络合物与反应物最低势能之差,E0是 60 50 两者零点能之间的差值。这个势能垒的存 BC 在说明了实验活化能的实质。 4、势能面投影图 A 将三维势能面投影到平面上,就得到 60 势能面的投影图。 65 图中曲线是相同势能的投影,称为等 势能线,线上数字表示等势能线的相对值, 等势能线的密集度表示势能变化的陡度。 靠坐标原点(O点)一方,随着原子核间距 图12.7势能面投影图
另一种是 Sato 又在这个基础上进行了修正,使势垒顶端不合理的势阱消失,这样得到 的势能面称为 London-Eyring-Polanyi-Sato 势能面,简称 LEPS 势能面。 如何获得势能面(意义和用途) 对于一个基元反应,如果能准确地获得势能面,就能知道它过渡态的势能大小,从势 能面上推测最可能的反应途径,从过渡态势能面的位置可确定活化能,这将给出重要的反 应动力学信息。因此如何获得势能面就成为化学动力学的重要任务,不过,目前只能对简 单的基元反应得到准确的势能面。研究最多的是 H+H2 和 F+H2 反应。 获得势能面的方法有三种: (1) 纯理论方法 通过量子力学计算。每个原子和分子有薛定谔方程,然后用量子 力学求解得到势能面。 (2) 半经验方法 也源于量子力学,但它应用了经验的双原子分子的势能公式 —Morse 式: p e 0 0 E r D a r r a r r ( ) [exp{ 2 ( )} 2exp{ ( )}] = − − − − − (3) 纯经验方法:如 Morse 势能公式或其它经验公式。 2、马鞍点(saddle point) 在势能面上,活化络合物所处的位置 T 点称为马鞍点。 该点势能与反应物和生成物所处的稳定态能量 R 点和 P 点 相比是最高点,但与坐标原点一侧和 D 点的势能相比又是最低 点 如把势能面比作马鞍的话,则马鞍点处在马鞍的中心。从 反应物到生成物必须越过一个能垒。 3、反应坐标(reaction coordinate) 势能面 反应坐标是一个连续变化的参数,其每一个值 都对应于沿反应体系中各原子的相对位置。如在势 能面上,反应沿着 RT→TP 的虚线进行,反应进程 不同,各原子间相对位置也不同,体系的能量也不 同。 如以势能为纵坐标,反应坐标为横坐标,画出 的图可以表示反应过程中体系势能的变化,这是一 条能量最低的途径。 沿势能面上 R-T-P 虚线切剖面图,把 R-T-P 曲 线作横坐标,这就是反应坐标。以势能作纵坐标,标出反应进程中每一点的势能,就得到 势能面的剖面图。 从反应物 A+BC 到生成物走的是能量 最低通道,但必须越过势能垒 Eb,Eb 是 活化络合物与反应物最低势能之差,E0 是 两者零点能之间的差值。这个势能垒的存 在说明了实验活化能的实质。 4、势能面投影图 将三维势能面投影到平面上,就得到 势能面的投影图。 图中曲线是相同势能的投影,称为等 势能线,线上数字表示等势能线的相对值, 等势能线的密集度表示势能变化的陡度。 靠坐标原点(O 点)一方,随着原子核间距 E0 Eb A+BC AB+C A B C≠ 反应坐标 势 能 E0 Eb A+BC AB+C A B C 图 12.7 势能面投影图 O D AB r BC r P R T ≠ T 706050506065