《电磁场理论》课程电子教案（讲义）第二章 电磁场的基本规律

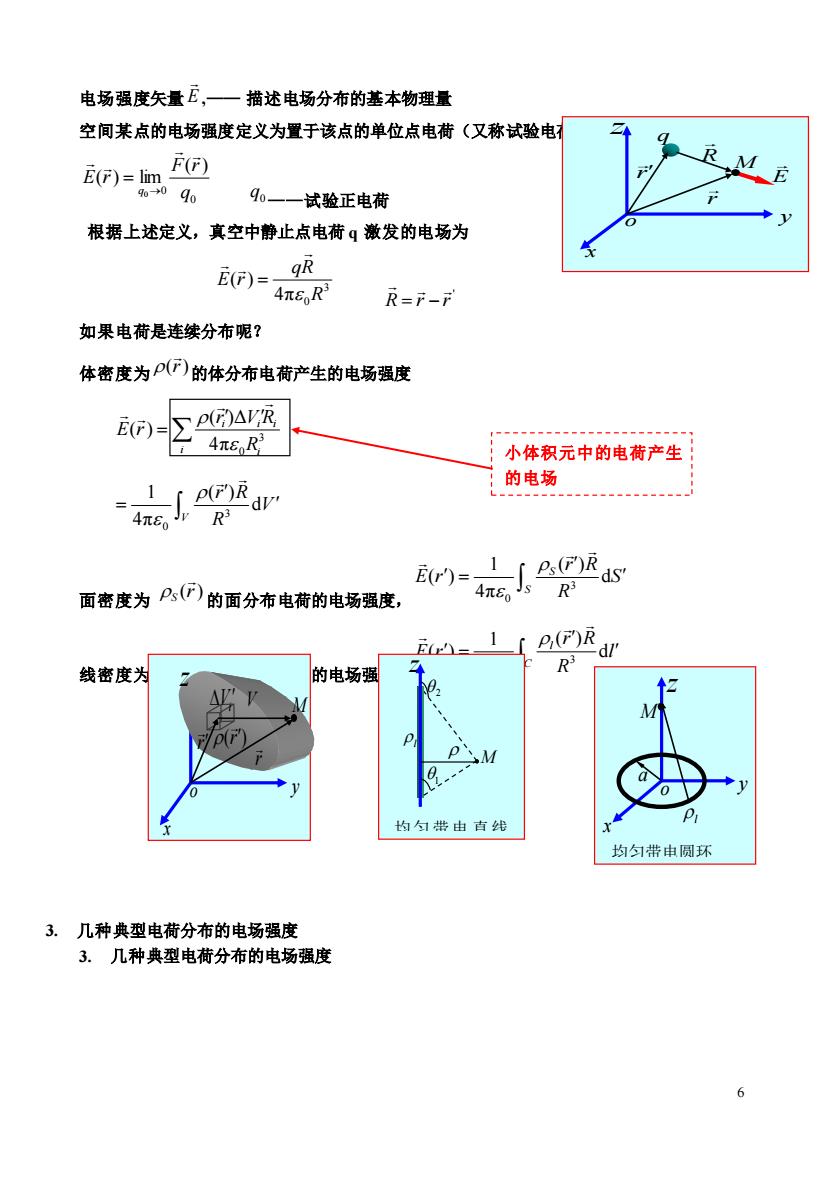
电场强度矢量E,一描述电场分布的基本物理量 空间某点的电场强度定义为置于该点的单位点电荷（又称试验电 前婴 M 90一一试验正电荷 根据上述定义，真空中静止点电荷q激发的电场为 gR E0)=4G,R R=F-r 如果电荷是连续分布呢？ 体密度为P)的体分布电荷产生的电场强度 E)=∑py见 4π8R 小体积元中的电荷产生 的电场 -dV R3 面密度为P,的面分布电荷的电场强度， E(r)=)s R E= 线密度为 的电场强 均匀带由直线 均匀带电圆环 3.几种典型电荷分布的电场强度 3.几种典型电荷分布的电场强度 6

6 电场强度矢量 E  ,—— 描述电场分布的基本物理量 空间某点的电场强度定义为置于该点的单位点电荷（又称试验电荷）受到的作用力，即 0 0 ( ) ( ) lim 0 q F r E r q     → = 0 q ——试验正电荷 根据上述定义，真空中静止点电荷 q 激发的电场为 3 4π 0 ( ) R qR E r     = ' R r r    = − 如果电荷是连续分布呢？ 体密度为 (r)   的体分布电荷产生的电场强度    = i i i i i R r V R E r 3 4π 0 ( )Δ ( )          = V V R r R d ( ) 4π 1 3 0     面密度为 (r) S   的面分布电荷的电场强度，     = S S S R r R E r d ( ) 4π 1 ( ) 3 0      线密度为 (r) S   的线分布电荷的电场强度，     = C l l R r R E r d ( ) 4π 1 ( ) 3 0      3. 几种典型电荷分布的电场强度 3. 几种典型电荷分布的电场强度 y x z o r  q r R E M 小体积元中的电荷产生 的电场 ( ) r  V y x z o r  Vi   r M l 1   z M 2  均匀带电 直线 段 l y x z o M a 均匀带电圆环

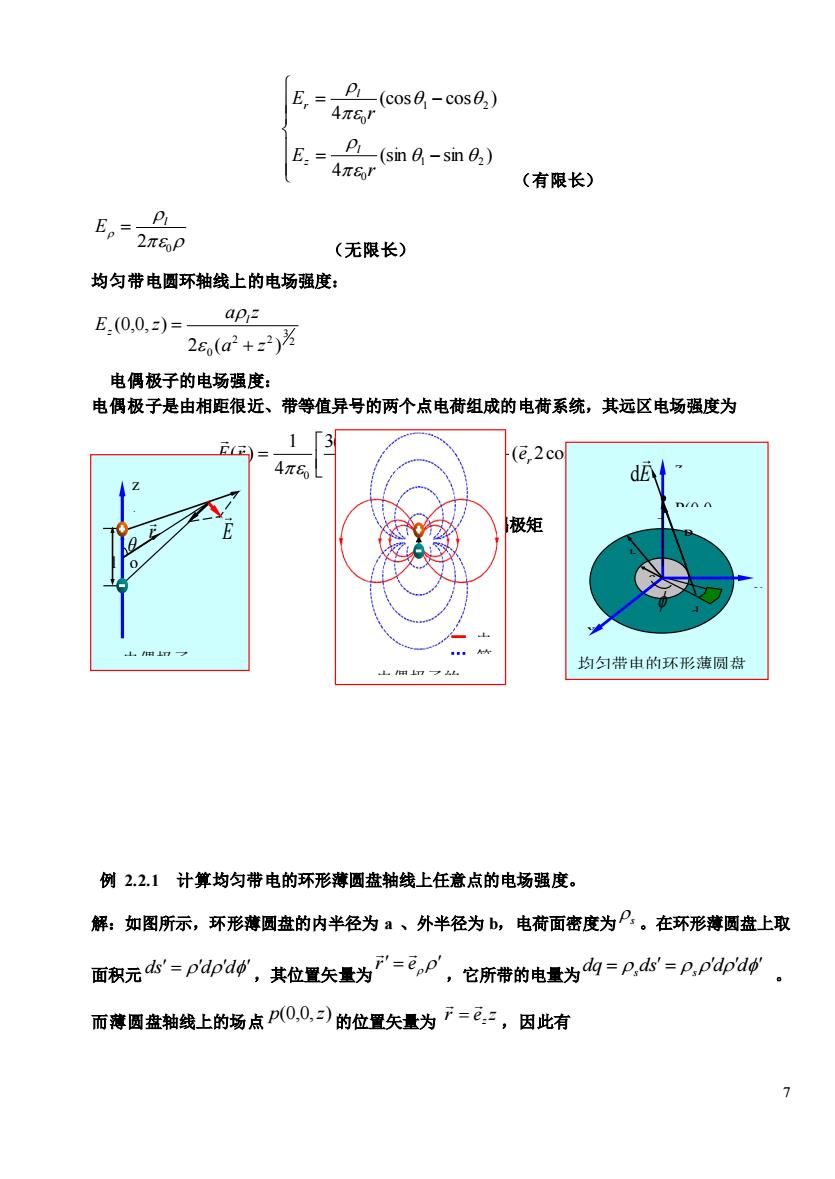
P(cos0,-cos0;) E,4 P(sin 0-sin 0;) E4r (有限长) E,2 (无限长) 均匀带电圆环轴线上的电场强度： E.(0,0,)= ap 2c(a2+z23 电偶极子的电场强度： 电偶极子是由相距很近、带等值异号的两个点电荷组成的电荷系统，其远区电场强度为 1 3 (e.2co π6 极矩 均匀带由的环形薄圆盘 例221计算均匀带电的环形薄圆盘轴线上任意点的电场强度。 解：如图所示，环形薄圆盘的内半径为a、外半径为b,电荷面密度为P。在环形薄圆盘上取 面积元dk=ppa0,其位置矢量为'=e,D,它所带的电量为d内=p,本=.dp 而薄圆盘轴线上的场点P0,0,)的位置矢量为F=:,因此有

7        = − = − (sin sin ) 4 (cos cos ) 4 1 2 0 1 2 0           r E r E l z l r （有限长）     2 0 l E = （无限长） 均匀带电圆环轴线上的电场强度： 2 3 2 2 0 2 ( ) (0,0, ) a z a z E z l z + =   电偶极子的电场强度： 电偶极子是由相距很近、带等值异号的两个点电荷组成的电荷系统，其远区电场强度为 ( 2cos sin ) 4 3( ) 4 1 ( ) 3 0 5 3 0        e e r p r p r p r r E r r         = +       −  = p ql   = ——电偶极矩 例 2.2.1 计算均匀带电的环形薄圆盘轴线上任意点的电场强度。 解：如图所示，环形薄圆盘的内半径为 a 、外半径为 b，电荷面密度为 s 。在环形薄圆盘上取 面积元 ds  = dd ，其位置矢量为 r  = e   ，它所带的电量为 dq =  ds  =  dd s s 。 而薄圆盘轴线上的场点 p(0,0,z) 的位置矢量为 r e zz   = ，因此有  r E + q 电偶极子 z l o － q 电偶极子的 场图 等 位 线 电 场 线 P(0,0, z) b r R y z x 均匀带电的环形薄圆盘 d S  a dE

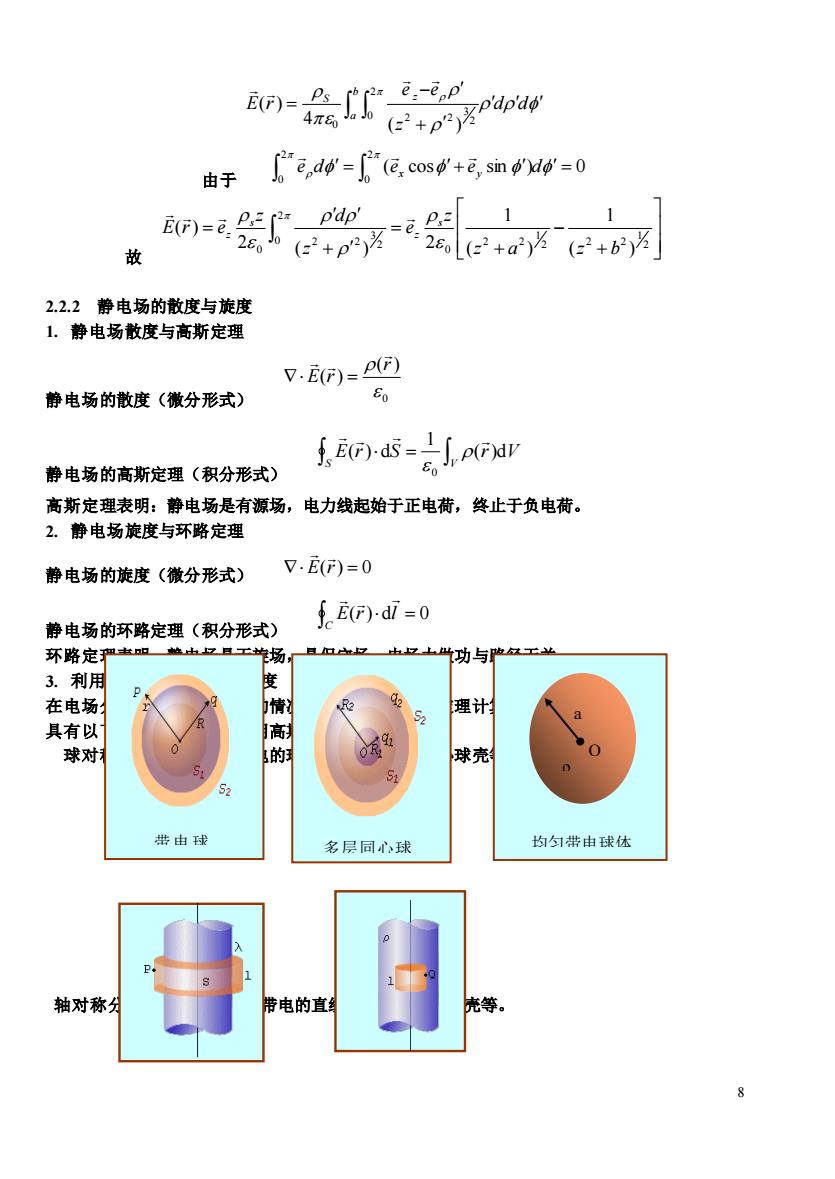
n-afraww 由于 do"(cos,si 1 年 、=62+03=g1 F2e2+a27(e2+6」 2.2.2静电场的散度与旋度 1.静电场散度与高斯定理 .E)= 静电场的散度（徽分形式） 60 静电场的高斯定理（积分形式） 美，i5- 高斯定理表明：静电场是有源场，电力线起始于正电荷，终止于负电荷。 2.静电场旋度与环路定理 静电场的旋度（微分形式） V.E)=0 静电场的环路定理（积分形式） fE0)-d=0 环路定严 功与■ 3.利用 度 在电场 理计」 具有以 球对 的 球壳 带由 名层同球 均匀带由球休 轴对称 寺电的直

8              +  −  =   d d z e e E r b a S z 2 0 2 3 2 2 0 ( ) 4 ( )     由于 ( cos sin ) 0 2 0 2 0  =  +   =         ed ex ey d    故         + − + = +    =  2 1 2 2 2 1 2 2 0 2 0 2 3 2 2 0 ( ) 1 ( ) 1 2 ( ) 2 ( ) z a z b z e z z d E r e s z s z             2.2.2 静电场的散度与旋度 1. 静电场散度与高斯定理 静电场的散度（微分形式） 0 ( ) ( )   r E r     = 静电场的高斯定理（积分形式）    = S V E r S (r)dV 1 ( ) d 0       高斯定理表明：静电场是有源场，电力线起始于正电荷，终止于负电荷。 2. 静电场旋度与环路定理 静电场的旋度（微分形式） E(r) = 0   静电场的环路定理（积分形式） ( )d = 0 C E r l    环路定理表明：静电场是无旋场，是保守场，电场力做功与路径无关。 3. 利用高斯定理计算电场强度 在电场分布具有一定对称性的情况下，可以利用高斯定理计算电场强度。 具有以下几种对称性的场可用高斯定理求解： 球对称分布：包括均匀带电的球面，球体和多层同心球壳等。 轴对称分布：如无限长均匀带电的直线，圆柱面，圆柱壳等。 带电球 壳 多层同心球 壳 均匀带电球体 a O ρ 0

无限大平面电荷：如无限大的均匀带电平面、平板等。 例2.2.2求真空中均匀带电球体的场强分布。已知球体半径为a,电有 解：(1)球外某点的场强 由于 (2)求球体内一点的场强 由于 iEd-Ag→ 4rEa万r→E=0) 2.3真空中恒定磁场的基本规律 本节内容 2.31安培力定律磁感应强度 2.3.2恒定磁场的散度与旋度 2.3.1安培力定律磁感应强度 1.安培力定律 安培对电流的磁效应进行了大量的实验研究，在1821一1825年之间，设计并完成了电 流相互作用的精巧实验，得到了电流相互作用力公式，称为安培力定律， 实验表明，真空中的载流回路C1对载流回路C2的作用力 后会人xE 安培力定律 R 载流回路C2对载流回路C1的作用力1=-斤。 ←一满足牛顿第三定律 2.磁感应强度 电流在其周围空间中产生磁场，描述磁场分布的基本物理量是磁感应强度B,单位为T(特 斯拉)。 磁场的重要特征是对场中的电流磁场力作用，载流回路C1对载流回路C2的作用力是回 路C1中的电流Ⅱ产生的磁场对回路C2中的电流2的作用力。 根据安培力定律，有

9 无限大平面电荷：如无限大的均匀带电平面、平板等。 例 2.2.2 求真空中均匀带电球体的场强分布。已知球体半径为 a ，电 荷密度为 0 。 解：（1）球外某点的场强 由于 0 3 0 0 π 3 1 4 d    a q E S S  = =    ( r a ) 3 2 0 3 0 =  r a E   （2）求球体内一点的场强 由于 E S V S V  = d 1 d 0 0     3 3 0 2 π 3 4 4π 3 1 4 r a q r E =     ( ) 3 0 0 r a r E =    2.3 真空中恒定磁场的基本规律 本节内容 2.3.1 安培力定律 磁感应强度 2.3.2 恒定磁场的散度与旋度 2.3.1 安培力定律 磁感应强度 1. 安培力定律 安培对电流的磁效应进行了大量的实验研究，在 1821 —1825 年之间，设计并完成了电 流相互作用的精巧实验，得到了电流相互作用力公式，称为安培力定律。 实验表明，真空中的载流回路 C1 对载流回路 C2 的作用力     = 2 1 3 12 0 2 2 1 1 12 12 d ( d ) 4π C C R I l I l R F      载流回路 C2 对载流回路 C1 的作用力 F21 F12   = − 2. 磁感应强度 电流在其周围空间中产生磁场，描述磁场分布的基本物理量是磁感应强度 B  ，单位为 T（特 斯拉）。 磁场的重要特征是对场中的电流磁场力作用，载流回路 C1 对载流回路 C2 的作用力是回 路 C1 中的电流 I1 产生的磁场对回路 C2 中的电流 I2 的作用力。 根据安培力定律，有 a r 0 r r E a 安培力定律 满足牛顿第三定律

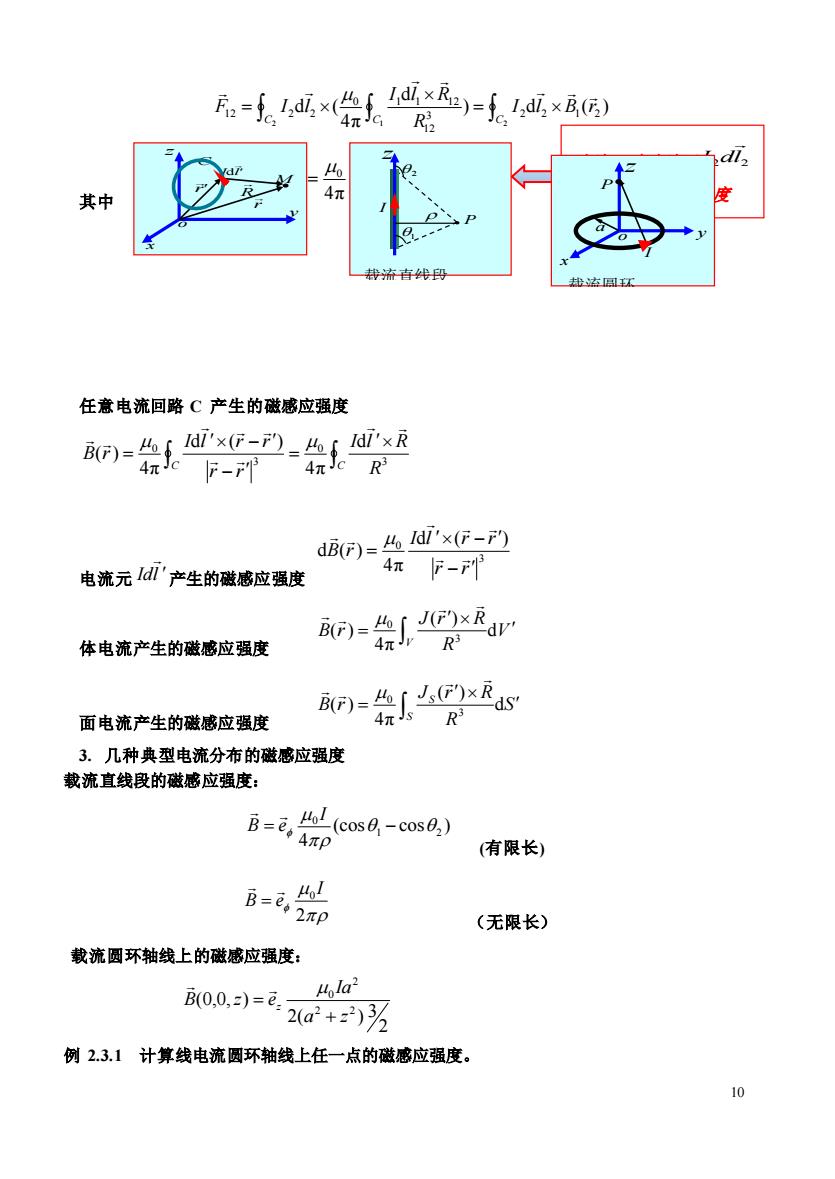
尼-.哈1，)-1感园 任意电流回路C产生的磁感应强度 n-会P-会10 C R d)='x(FF) 电流元I'产生的磁感应强度 4πF- 体电流产生的磁感应强度 i)av F)()xRas 面电流产生的磁感应强度 4πJ R 3.几种典型电流分布的磁感应强度 载流直线段的磁感应强度： (coco.) (有限长) Bn (无限长) 载流圆环轴线上的磁感应强度： ula2 0.0,）=0202+)% 例2.3.1计算线电流圆环轴线上任一点的磁感应强度。 10

10    =   =  2 1 2 ) d ( ) d 4π d ( 3 2 2 1 2 12 0 1 1 12 12 2 2 C C C I l B r R I l R F I l         其中   = 1 3 12 0 1 1 12 1 2 d 4π ( ) C R I l R B r      任意电流回路 C 产生的磁感应强度    = −   −  = C C R I l R r r I l r r B r 3 0 3 0 d 4π d ( ) 4π ( )            电流元 Idl   产生的磁感应强度 3 0 d ( ) 4π d ( ) r r I l r r B r −   −  =         体电流产生的磁感应强度 V R J r R B r V    =  d ( ) 4π ( ) 3 0      面电流产生的磁感应强度 S R J r R B r S S    =  d ( ) 4π ( ) 3 0      3. 几种典型电流分布的磁感应强度 载流直线段的磁感应强度： (cos cos ) 4 1 2 0      =  − I B e   (有限长)    2 0 I B e   = （无限长） 载流圆环轴线上的磁感应强度： 2 3 2( ) (0,0, ) 2 2 2 0 a z Ia B z ez + =    例 2.3.1 计算线电流圆环轴线上任一点的磁感应强度。 电流 I1在电流元 2 2 I dl  处产生的磁感应强度 y x z o r  Il d  r R C M I 1  z P  2 载流直线段 I y x z o P a 载流圆环